când o fracție „normală” conține fracții fie în numărător, fie în numitor, fie în ambele, atunci considerăm că este o fracție complexă. Acest tip de fracție este, de asemenea, cunoscut sub numele de fracție compusă.există două metode utilizate pentru a simplifica un astfel de tip de fracție.
Metoda 1
etape-Cheie:
- de a Crea o singură fracție, la numărător și numitor.,
- aplicați regula de divizare a fracțiilor înmulțind numărătorul cu inversul sau inversul numitorului.
- Simplificați, dacă este necesar.
Metoda 2
etape-Cheie:
- a Gasi cel mai mic Numitor Comun (LCD) de toți numitorii în fracțiunile complexe.
- înmulțiți acest LCD cu numărătorul și numitorul fracției complexe.
- Simplificați, dacă este necesar.,
după ce parcurgeți câteva exemple, ar trebui să vă dați seama că metoda 2 este mult mai bună decât metoda 1, deoarece aproape întotdeauna este nevoie de mai puțini pași pentru a ajunge la răspunsul final.
Exemple de simplificare a fracțiilor complexe
Exemplul 1: Simplificați fracția complexă de mai jos.
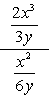
- se Utilizează Metoda 1
Atât numărătorul cât și numitorul complex fracțiune sunt deja exprimate ca singur fracțiuni. E grozav!,

următorul pas să faceți este să se aplice regula divizia înmulțind numărătorul de reciprocitate de la numitor. Finalizați prin anularea factorilor comuni pentru a obține răspunsul final.
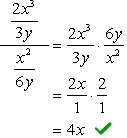
- Folosind Metoda 2
Găsi LCD de întreaga problemă, că este, LCD-ul de sus și de jos numitori.,

de la LCD de 3y și 6y este doar \textbf{6y}, vom multiplica complex numărătorul și numitorul cu acest LCD. După aceasta, ne putem aștepta ca problema să fie redusă la o singură fracție care poate fi simplificată ca de obicei.
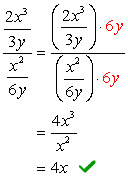
Exemplu 2: Simplificarea procesului complex de fracțiune de mai jos.,
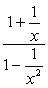
- se Utilizează Metoda 1
În această metodă, ne-o dorim pentru a crea o singură fracțiune atât la numărător și numitor. Evident, această problemă ne-ar cere să facem asta mai întâi înainte de a efectua diviziunea.
adăugați fracțiile în numărător și scădeți cele din numitor.,
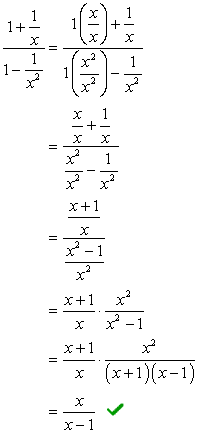
- Folosind Metoda 2
se Uită la numitori \large{x} și \large{x^2}, sa LCD trebuie să fie \large{x^2} Multiplica de sus și de jos de acest LCD.
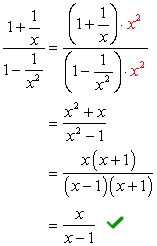
Exemplul 3: Simplificarea procesului complex de fracțiune de mai jos.,
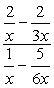
- se Utilizează Metoda 1
Crea singur fracțiuni în atât numărătorul cât și numitorul, apoi urmați prin împărțirea fracțiilor.
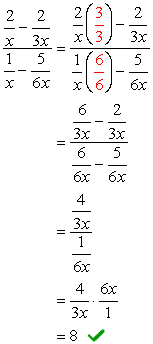
- Folosind Metoda 2
ansamblu LCD al numitorilor este \color{red}6x. Utilizați această pentru a se multiplica prin partea de sus și de jos expresii.,
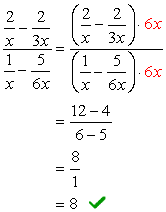
Exemplul 4: Simplificarea procesului complex de fracțiune de mai jos.
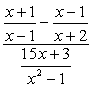
Pentru această problemă, vom folosi Metoda 1 numai.problema necesită aplicarea metodei foliei (înmulțirea a două binomiale) și o simplă factorizare a trinomului. Poate părea un pic intimidant la început; cu toate acestea, dacă acordați atenție detaliilor, vă garantez că nu este atât de rău.,dacă observați, numitorul complex este deja în forma pe care o dorim – având un simbol fracțional. Aceasta înseamnă că trebuie să lucrăm puțin la numărătorul complex. Următorul pas ar fi transformarea numărătorului complex într-o fracție” simplă ” sau unică.
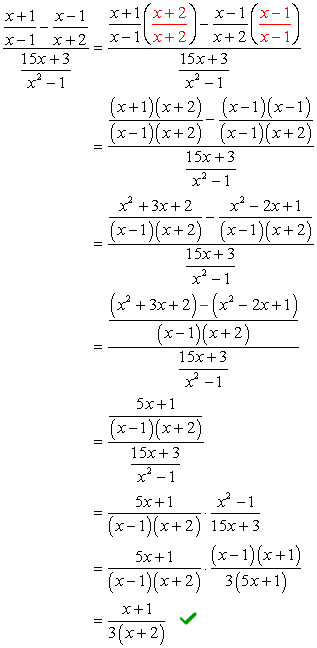
Exemplul 5: să Simplifice complexul fracțiune de mai jos.
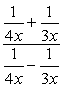
Pentru această problemă, vom folosi Metoda 2 numai.,
observați că ecranul LCD al tuturor numitorilor este doar \color{red}12x. utilizați acest lucru ca multiplicator comun atât pentru expresiile de sus, cât și pentru cele de jos.
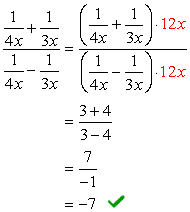
Practica cu Foi de lucru
s-ar putea fi, de asemenea, interesat în:
Înmulțirea Fracțiunile Complexe
Împărțirea Numere Complexe