de 5 Klustringsalgoritmerna Dataforskare behöver veta

Jag startade nyligen ett bokfokuserat pedagogiskt nyhetsbrev. Book Dives är ett nyhetsbrev varannan vecka där vi för varje ny utgåva dyker in i en facklitteratur bok. Du lär dig om bokens kärnlektioner och hur du applicerar dem i verkligheten. Du kan prenumerera på det här.

kluster är en maskininlärningsteknik som innebär gruppering av datapunkter. Med tanke på en uppsättning datapunkter kan vi använda en klusterningsalgoritm för att klassificera varje datapunkt i en viss grupp., I teorin bör datapunkter som finns i samma grupp ha liknande egenskaper och/eller egenskaper, medan datapunkter i olika grupper ska ha mycket olika egenskaper och/eller egenskaper. Klustring är en metod för oövervakad inlärning och är en vanlig teknik för statistisk dataanalys som används inom många områden.

i datavetenskap kan vi använda klusteranalys för att få några värdefulla insikter från våra data genom att se vilka grupper datapunkterna faller in i när vi tillämpar en klusteringsalgoritm., Idag ska vi titta på 5 populära klustringsalgoritmer som Dataforskare behöver veta och deras fördelar och nackdelar!

k-Means klustring

K-Means är förmodligen den mest kända klustringsalgoritmen. Det lärs i en hel del inledande datavetenskap och maskininlärning klasser. Det är lätt att förstå och implementera i kod! Kolla in bilden nedan för en illustration.,

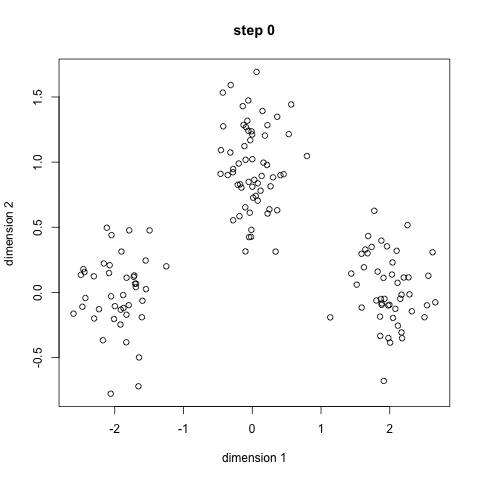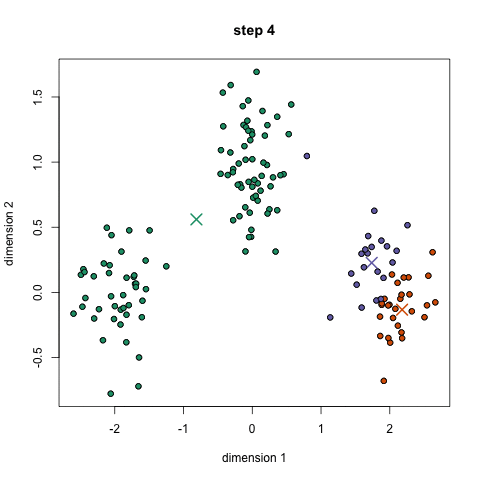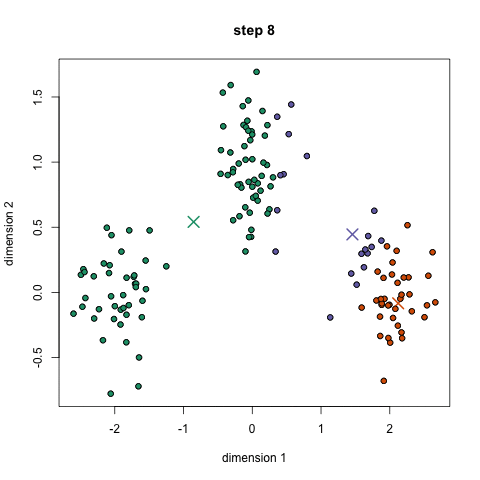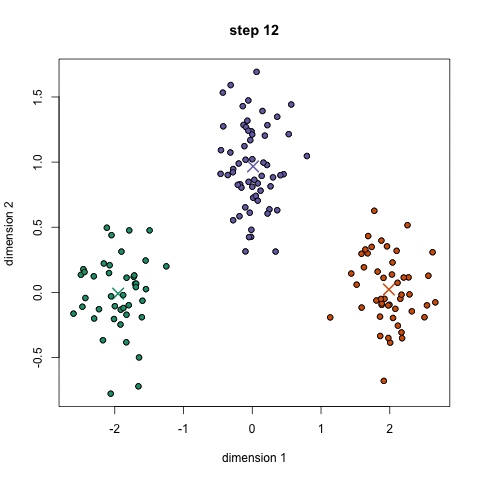
1. till att börja med väljer vi först ett antal klasser/grupper att använda och slumpmässigt initiera sina respektive mittpunkter. För att räkna ut antalet klasser att använda är det bra att ta en snabb titt på data och försöka identifiera några distinkta grupperingar. Mittpunkterna är vektorer av samma längd som varje datapunktsvektor och är ”X” i grafiken ovan.,
2. varje datapunkt klassificeras genom att beräkna avståndet mellan den punkten och varje gruppcenter och sedan klassificera punkten att vara i den grupp vars centrum ligger närmast den.
3. baserat på dessa klassificerade punkter omkomputerar vi gruppcentret genom att ta medelvärdet av alla vektorer i gruppen.
4. upprepa dessa steg för ett visst antal iterationer eller tills gruppcentralerna inte ändras mycket mellan iterationer. Du kan också välja att slumpmässigt initiera gruppcentra några gånger och välj sedan körningen som ser ut som den gav de bästa resultaten.,

K-Means har fördelen att det är ganska snabbt, eftersom allt vi verkligen gör är att beräkna avstånden mellan punkter och gruppcentra; mycket få beräkningar! Den har således en linjär komplexitet O (n).

å andra sidan har K-Means ett par nackdelar. För det första måste du välja hur många grupper/klasser det finns. Detta är inte alltid trivialt och helst med en klustringsalgoritm som vi vill att det ska räkna ut för oss eftersom poängen med det är att få lite insikt från data., K-means börjar också med ett slumpmässigt urval av klustercentraler och därför kan det ge olika klusterresultat på olika körningar av algoritmen. Således kan resultaten inte vara repeterbara och saknar konsistens. Andra klustermetoder är mer konsekventa.

k-Medians är en annan klusterningsalgoritm relaterad till K-Means, förutom i stället för att komputera gruppcentralpunkterna med hjälp av medelvärdet vi använder gruppens medianvektor., Denna metod är mindre känslig för avvikare (på grund av att medianen används) men är mycket långsammare för större datauppsättningar eftersom sortering krävs på varje iteration vid beräkning av Medianvektorn.

Mean-Shift Clustering

Mean shift clustering är en glidande fönsterbaserad algoritm som försöker hitta täta områden av datapunkter. Det är en centroid-baserad algoritm vilket innebär att målet är att lokalisera mittpunkterna i varje grupp/klass, som fungerar genom att uppdatera kandidater för mittpunkter för att vara medelvärdet av punkterna i skjutfönstret., Dessa kandidatfönster filtreras sedan i ett efterbehandlingsstadium för att eliminera nära dubbletter, som bildar den slutliga uppsättningen mittpunkter och deras motsvarande grupper. Kolla in bilden nedan för en illustration.

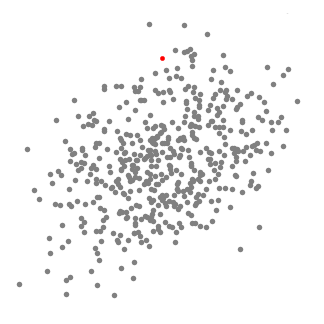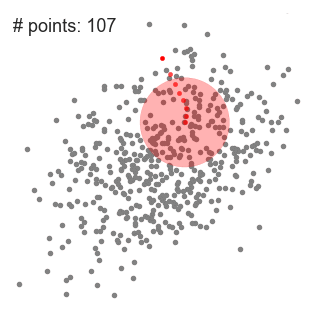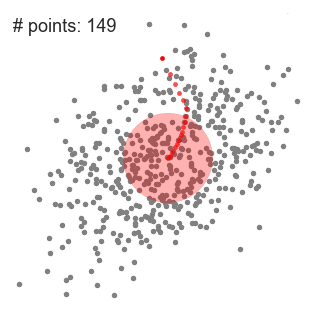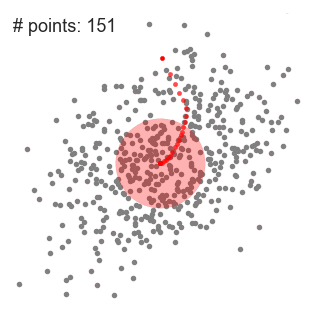
1. för att förklara mean-shift kommer vi att överväga en uppsättning punkter i tvådimensionellt utrymme som ovanstående illustration., Vi börjar med ett cirkulärt skjutfönster centrerat vid en punkt c (slumpmässigt vald) och har radie r som kärnan. Mean shift är en hill-klättring algoritm som innebär att flytta denna kärna iterativt till en högre densitet region på varje steg tills konvergens.
2. vid varje iteration flyttas skjutfönstret mot regioner med högre densitet genom att flytta mittpunkten till medelvärdet av punkterna i fönstret (därav namnet). Densiteten i skjutfönstret är proportionell mot antalet punkter inuti den., Naturligtvis, genom att flytta till medelvärdet av punkterna i fönstret kommer det gradvis att röra sig mot områden med högre punktdensitet.
3. vi fortsätter att flytta skjutfönstret enligt medelvärdet tills det inte finns någon riktning där ett skift kan rymma fler punkter inuti kärnan. Kolla in grafiken ovan; vi fortsätter att flytta cirkeln tills vi inte längre ökar densiteten (d.v.s. antal punkter i fönstret).
4. denna process av steg 1 till 3 görs med många skjutbara fönster tills alla punkter ligger inom ett fönster., När flera skjutfönster överlappar fönstret som innehåller flest punkter bevaras. Datapunkterna är sedan grupperade enligt skjutfönstret där de bor.

en illustration av hela processen från slutet till slutet med alla skjutbara fönster visas nedan. Varje svart prick representerar centroid av ett skjutfönster och varje grå prick är en datapunkt.,

i motsats till k-means clustering behöver du inte välja antalet kluster som mean-shift upptäcker automatiskt detta. Det är en stor fördel. Det faktum att klustercentra konvergerar mot punkterna med maximal densitet är också ganska önskvärt eftersom det är ganska intuitivt att förstå och passar bra i en naturligt datadriven mening., Nackdelen är att valet av fönsterstorlek / radie ” r ” kan vara icke-trivialt.

Densitetsbaserad rumslig klustring av applikationer med brus (DBSCAN)

DBSCAN är en täthetsbaserad klustrad algoritm som liknar mean-shift, men med ett par anmärkningsvärda fördelar. Kolla in en annan fancy grafik nedan och låt oss komma igång!,

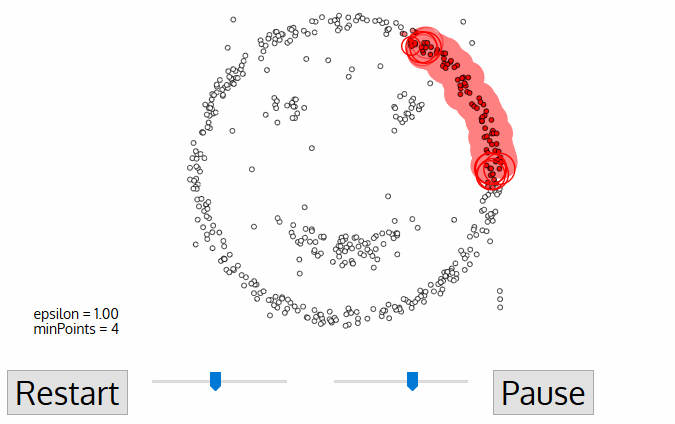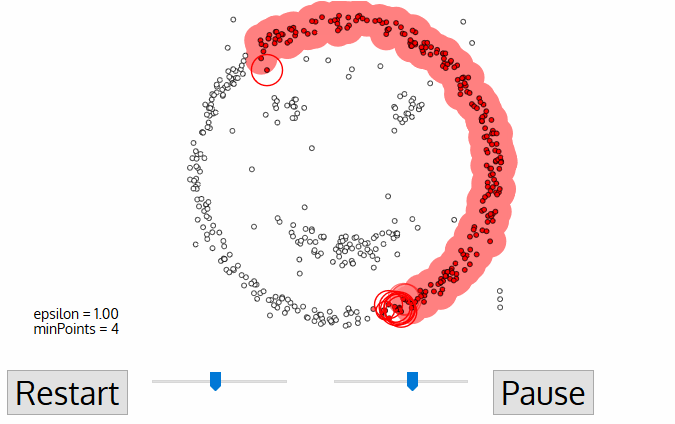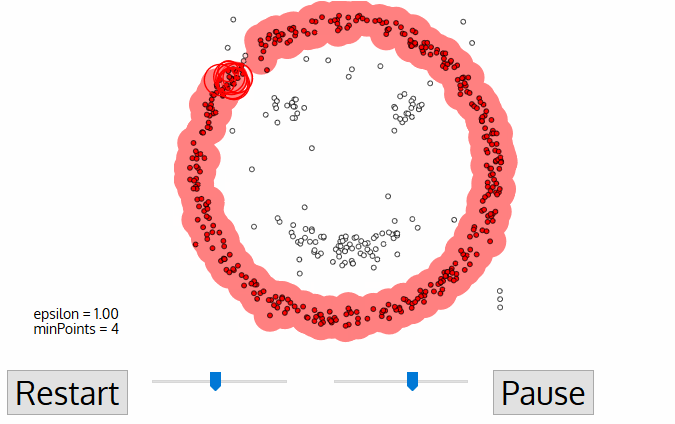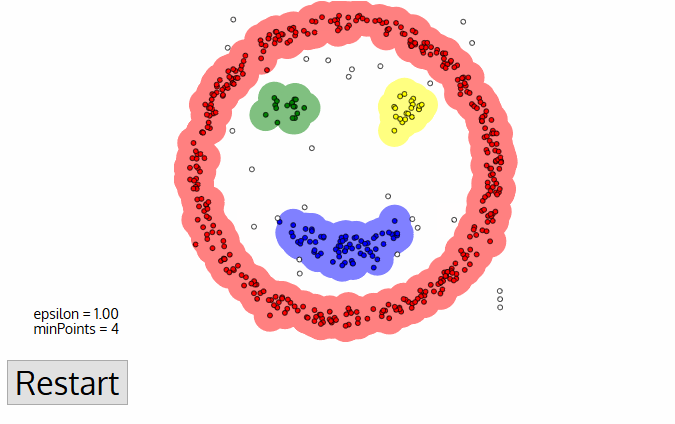
1. dbscan börjar med en godtycklig startdatapunkt som inte har besökts. Grannskapet av denna punkt extraheras med ett avstånd epsilon ε (alla punkter som ligger inom ε avstånd är grannskapspunkter).,
2. om det finns ett tillräckligt antal punkter (enligt minPoints) i detta område startar klustringsprocessen och den aktuella datapunkten blir den första punkten i det nya klustret. Annars kommer punkten att märkas som buller (senare kan denna bullriga punkt bli en del av klustret). I båda fallen markeras den punkten som ”besökt”.
3. för denna första punkt i det nya klustret blir punkterna inom dess ε-avstånd också en del av samma kluster., Denna procedur för att göra alla punkter i ε-kvarteret hör till samma kluster upprepas sedan för alla nya punkter som just har lagts till i klustergruppen.
4. denna process av steg 2 och 3 upprepas tills alla punkter i klustret bestäms dvs alla punkter inom ε-området i klustret har besökts och märkts.
5. när vi är klara med det aktuella klustret hämtas och bearbetas en ny ovisited punkt, vilket leder till upptäckten av ett ytterligare kluster eller brus. Denna process upprepas tills alla punkter är markerade som besökta., Eftersom alla punkter i slutet av detta har besökts, kommer varje punkt att ha markerats som antingen tillhör ett kluster eller som buller.

DBSCAN innebär några stora fördelar jämfört med andra klustringsalgoritmer. För det första kräver det inte ett pe-set antal kluster alls. Det identifierar också outliers som ljud, till skillnad från mean-shift som helt enkelt slänger dem i ett kluster även om datapunkten är väldigt annorlunda. Dessutom kan det hitta godtyckligt stora och godtyckligt formade kluster ganska bra.,

den största nackdelen med DBSCAN är att den inte fungerar lika bra som andra när klustren är av varierande densitet. Detta beror på att inställningen av avståndsgränsen ε och minPoints för att identifiera grannskapspunkterna varierar från kluster till kluster När densiteten varierar. Denna nackdel uppstår också med mycket högdimensionella data eftersom avståndet tröskeln ε blir utmanande att uppskatta.,

förväntan–maximering (EM) kluster med Gaussisk blandning modeller (GMM)

en av de största nackdelarna med K-medel är dess naiva användning av medelvärdet för klustercentret. Vi kan se varför detta inte är det bästa sättet att göra saker genom att titta på bilden nedan. På vänster sida ser det ganska uppenbart för det mänskliga ögat att det finns två cirkulära kluster med olika radie ” centrerad på samma sätt. K-Means kan inte hantera detta eftersom medelvärdena för klustren är mycket nära varandra., K-Means misslyckas också i fall där klustren inte är cirkulära, igen som ett resultat av att använda medelvärdet som klustercenter.

Gauss blandning modeller (GMM) ger oss mer flexibilitet än K-medel. Med GMM antar vi att datapunkterna distribueras Gaussian; detta är ett mindre restriktivt antagande än att säga att de är cirkulära med hjälp av medelvärdet., På så sätt har vi två parametrar för att beskriva formen på klustren: medelvärdet och standardavvikelsen! Med ett exempel i två dimensioner betyder det att klustren kan ta någon form av elliptisk form (eftersom vi har en standardavvikelse i både X-och y-riktningarna). Således tilldelas varje Gaussisk fördelning till ett enda kluster.

för att hitta parametrarna för Gaussian för varje kluster (t.ex.medelvärdet och standardavvikelsen), kommer vi att använda en optimeringsalgoritm som kallas förväntan–maximering (EM)., Ta en titt på bilden nedan som en illustration av Gaussierna som är monterade på klustren. Då kan vi fortsätta med processen med förväntan-maximering klustring med GMM.

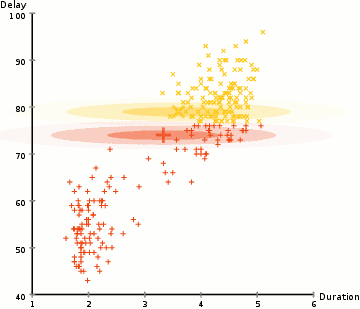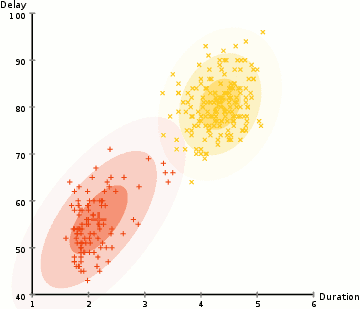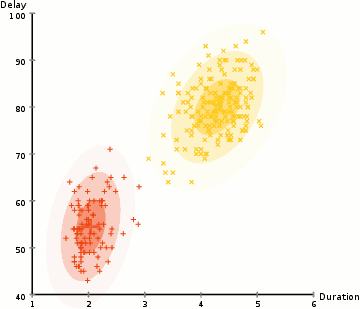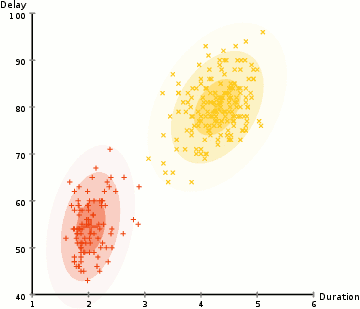
1. vi börjar med att välja antalet kluster (som k-means gör) och slumpmässigt initiera de gaussiska distributionsparametrarna för varje kluster., Man kan försöka ge en bra guesstimate för de ursprungliga parametrarna genom att ta en snabb titt på data också. Även notera, som kan ses i bilden ovan, är detta inte 100% nödvändigt eftersom Gaussierna börjar vår som mycket dålig men snabbt optimeras.
2. med tanke på dessa Gaussfördelningar för varje kluster, beräkna sannolikheten för att varje datapunkt tillhör ett visst kluster. Ju närmare en punkt är till gaussians centrum, desto mer sannolikt hör det till det klustret., Detta bör göra intuitiv mening eftersom vi med en Gaussisk distribution antar att de flesta data ligger närmare mitten av klustret.
3. baserat på dessa sannolikheter beräknar vi en ny uppsättning parametrar för de gaussiska fördelningarna så att vi maximerar sannolikheterna för datapunkter i klustren. Vi beräknar dessa nya parametrar med hjälp av en viktad summa av datapunktspositionerna, där vikterna är sannolikheterna för datapunkten som hör till det specifika klustret., För att förklara detta visuellt kan vi ta en titt på bilden ovan, i synnerhet det gula klustret som ett exempel. Fördelningen börjar slumpmässigt vid den första iterationen, men vi kan se att de flesta av de gula punkterna är till höger om den fördelningen. När vi beräknar en summa viktad av sannolikheterna, även om det finns några punkter nära mitten, är de flesta till höger. Således skiftas naturligtvis distributionens medelvärde närmare dessa punkter. Vi kan också se att de flesta punkterna är ”övre högra till nedre vänstra”., Därför ändras standardavvikelsen för att skapa en ellips som är mer anpassad till dessa punkter för att maximera summan viktad av sannolikheterna.
4. steg 2 och 3 upprepas iterativt tills konvergens, där fördelningarna inte förändras mycket från iteration till iteration.

det finns 2 viktiga fördelar med att använda GMM. För det första är GMM mycket mer flexibla när det gäller klusterkovarians än K-medel.på grund av standardavvikelseparametern kan klustren ta på sig vilken ellipsform som helst, snarare än att vara begränsad till cirklar., K-Means är faktiskt ett speciellt fall av GMM där varje klusters kovarians längs alla dimensioner närmar sig 0. För det andra, eftersom GMM använder sannolikheter, kan de ha flera kluster per datapunkt. Så om en datapunkt ligger mitt i två överlappande kluster kan vi helt enkelt definiera sin klass genom att säga att den tillhör X-procent till klass 1 och Y-procent till klass 2. Dvs gmms stöder Blandat medlemskap.

Agglomerativ hierarkisk klustring

hierarkiska klustringsalgoritmer faller i 2 kategorier: uppifrån och ner eller nedifrån och upp., Bottom-up-algoritmer behandlar varje datapunkt som ett enda kluster i början och sedan successivt sammanfoga (eller agglomerat) par av kluster tills alla kluster har sammanfogats till ett enda kluster som innehåller alla datapunkter. Bottom-up hierarkisk klustring kallas därför hierarkisk agglomerativ klustring eller HAC. Denna hierarki av kluster representeras som ett träd (eller dendrogram). Trädets rot är det unika klustret som samlar alla prover, bladen är klustren med bara ett prov., Kolla in bilden nedan för en illustration innan du går vidare till algoritmstegen

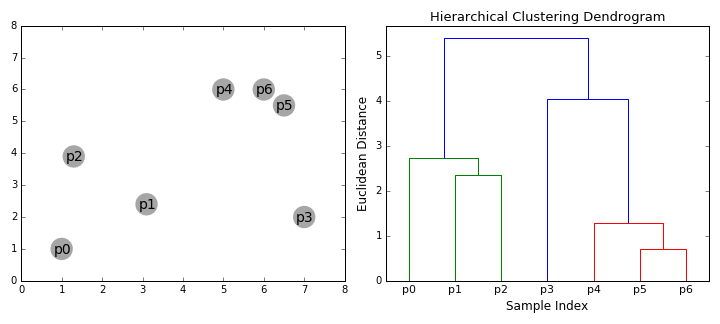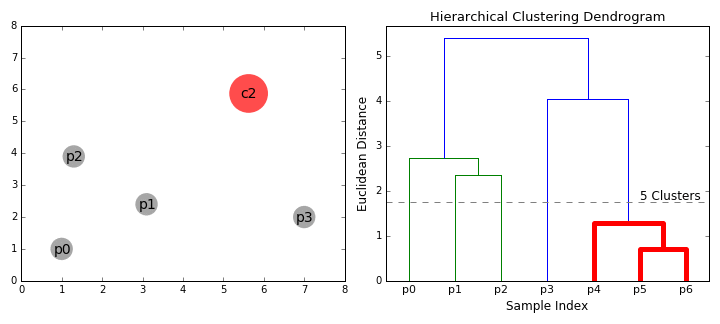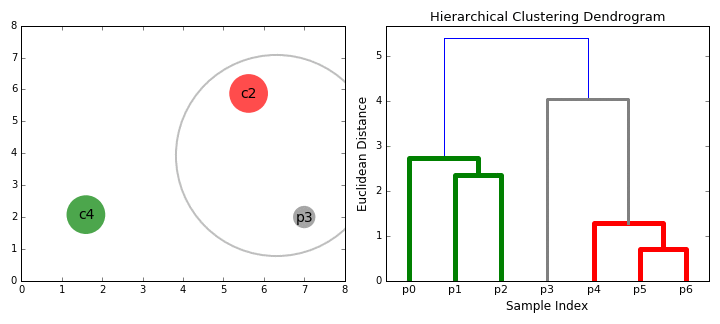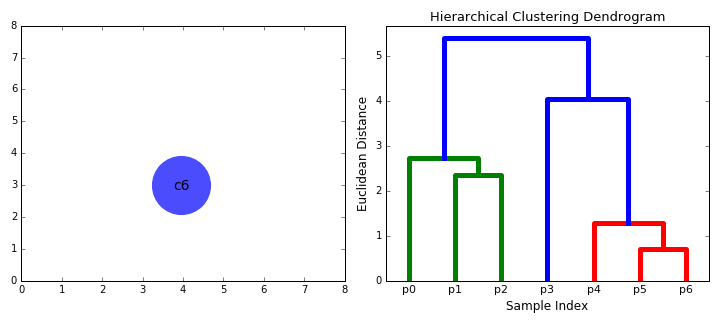
1. vi börjar med att behandla varje datapunkt som ett enda kluster dvs om det finns x-datapunkter i vår dataset så har vi x-kluster. Vi väljer sedan ett avståndsmått som mäter avståndet mellan två kluster., Som ett exempel kommer vi att använda Genomsnittlig koppling som definierar avståndet mellan två kluster för att vara det genomsnittliga avståndet mellan datapunkter i det första klustret och datapunkter i det andra klustret.
2. på varje iteration kombinerar vi två kluster i en. De två kluster som ska kombineras väljs som de med den minsta genomsnittliga kopplingen. Dvs enligt vårt valda avstånd metriska har dessa två kluster det minsta avståndet mellan varandra och är därför mest lika och bör kombineras.
3. steg 2 upprepas tills vi når roten av trädet i.,e vi har bara ett kluster som innehåller alla datapunkter. På så sätt kan vi välja hur många kluster vi vill ha i slutändan, helt enkelt genom att välja när vi ska sluta kombinera klustren dvs när vi slutar bygga trädet!

hierarkisk kluster kräver inte att vi anger antalet kluster och vi kan även välja vilket antal kluster som ser bäst ut eftersom vi bygger ett träd. Dessutom är algoritmen inte känslig för valet av avståndsmätning. alla tenderar att fungera lika bra medan med andra klusterningsalgoritmer är valet av avståndsmätning kritiskt., Ett särskilt bra användningsfall av hierarkiska klusterningsmetoder är när de underliggande data har en hierarkisk struktur och du vill återställa hierarkin; andra klusterningsalgoritmer kan inte göra detta. Dessa fördelar med hierarkisk clustering kommer till kostnaden för lägre effektivitet, eftersom den har en tidskomplexitet av O(n3), till skillnad från K-Means och GMM: s linjära komplexitet.