distributioner
kärnproblemet i hjärtat av problemen med Dirac delta och liknande
matematiska objekt är problemet med differentierbarhet. Som Dirac anges i citatet ovan, du egentligen inte köra i trubbel om du använder hans δ funktion som en symbolisk regel för hur det fungerar på andra funktioner; men fortsätter han att skilja δ i sina beräkningar, och det är där problemen verkligen börjar., Hur kan man veta a priori ”när dessa operationer är tillåtna” när man inte ens har en fast definition av objekten, eller vad det skulle innebära att skilja dem? Vi kommer att se hur dessa frågor leder till härledning av nya och noggrant definierade matematiska objekt.
funktionella
överväga hur man normalt bestämmer derivatet (eller antiderivatet) av en funktion. Under normala omständigheter, med ”klassiska” funktioner, har du en väldefinierad regel som beskriver hur en funktion kartlägger en uppsättning reella tal till en annan uppsättning, säg f: → Trip., Med tanke på detta och definitionerna av integralen eller derivatet kan man sedan tydligt undersöka de värden som dessa operatörer ger när de tillämpas på funktionen. När det gäller δ har vi ingen fungerande definition att gå vidare i denna riktning. I stället definieras δ i praktiken mest framträdande av hur det fungerar på andra, väldefinierade funktioner (som i (3)). Detta är den viktigaste insikten som leder till den moderna teorin om fördelningar. Det visar sig att det rätta sättet att matematiskt behandla δ, och en stor klass av liknande objekt, är att sluta försöka definiera dem som funktioner alls., Denna tankegång beskrivs väl av Jean Dieudonne i sin granskning av (Se ):
… man börjar med en familj med mycket ”vanliga” funktioner (vanligtvis med
avseende på differentialegenskaper), som uppfyller vissa (i allmänhet
integrerade) relationer, eller där vissa operationer är möjliga; och
då upptäcker man att en a priori större familj av funktioner uppfyller
samma relationer, eller kan utsättas för liknande operationer. Många
frågor då kan naturligtvis ställas: är denna nya familj verkligen
skiljer sig från den första?, Om det är, vad är relationerna mellan de två familjerna
, och kan man ge en exakt beskrivning av den nya?
det är bara i den sista etappen av ”förhistoria” att det som kan vara
kallas en revolutionerande synvinkel kommer att dyka upp, med tanken att
den ”nya familjen” kan bestå av andra objekt än funktioner.
de andra objekten som anspelas på är funktionella. Du kan tänka dig en funktionell
som en funktion av funktioner., Eftersom en funktion är en unik kartläggning från en uppsättning
– nummer till en annan, kan en funktionell F definieras som en kartläggning F : C →Trip,
där C är en uppsättning funktioner. Det vill säga en funktionell kartor fungerar till verkliga
siffror., Ett enkelt exempel på en funktion av denna typ är den bestämda integralen:

som tydligt tar en funktion F från någon uppsättning lämpligt integrerbara funktioner och kartlägger den till ett verkligt tal, värdet på integralet eller området under kurvan f(x) mellan A och B. Detta är bara ett enda exempel., Man kan föreställa sig ett oändligt antal funktionella, och uppsättningar av funktionella; man kan till och med fortsätta att generalisera och definiera mappningar från uppsättningar av funktionella till reella tal. Det är varken här eller där. Vad som är viktigt är att det funktionella konceptet kan användas för att definiera fördelningar.
uppsättningen testfunktioner
Vi kräver ytterligare en definition för att uppnå vårt mål. Detta innebär att ange uppsättningen C av funktioner från vilka distributionerna kommer att kartlägga funktioner till reella tal., Funktioner samlas ofta in i uppsättningar som anger deras grad av kontinuitet, differentierbarhet och kontinuiteten i deras derivat. Vi säger att en funktion f är i uppsättningen C (skriv C) om det är kontinuerligt över hela den verkliga linjen i den meningen att gränsen vid alla punkter är densamma när den tas från vänster eller höger; det är inte nödvändigtvis differentierbart. Vi säger att f. d. C1 om dess derivat existerar och är kontinuerligt, d.v. s. f. Till exempel är funktionen g(x) = |x| kontinuerlig men inte differentierbar vid x= 0; g är i C, men inte i C1., Vi kan generalisera detta och säga att Canis är den uppsättning funktioner som för kontinuerliga funktioner har sina första n-derivat, där n är ett heltal.
När n blir större blir uppsättningarna i en mening ”mindre;” Du kan alltid hitta funktioner (oändligt många!) som är i C: A men inte C: A 1. Dessa ”kontinuitetsutrymmen” bildar därför en sekvens av kapslade delmängder, som visas nedan.

nära botten av denna oändliga sekvens av uppsättningar av funktioner hittar vi uppsättningen
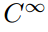
vilket naturligtvis är uppsättningen av alla funktioner som har oändligt många kontinuerliga derivat. Många välkända och vänliga funktioner finns i denna senare klass(t.ex. sin(x); cos (x); e, alla polynom)., Dessa funktioner kallas ”släta” eller ”väluppfostrade” eftersom man kan utföra differentieringens funktion på dem så många gånger som man trivs utan vård. Men även om denna uppsättning verkligen har oändligt många medlemmar, de är sällsynta i den meningen att de flesta funktioner är inte så väluppfostrade.
den uppsättning som är lämplig för definitionen av distributioner är ännu mindre
än detta. Det kräver ytterligare ett kriterium: att funktionerna har kompakt stöd. Denna tekniska term innebär helt enkelt att en funktion har icke-nollvärden inom en ändlig domän, och är likformigt noll utanför detta., Vi använder därför notationen
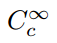
för att beteckna uppsättningen av steglöst kontinuerligt differentierbara funktioner med kompakt stöd, och kalla sådana funktioner testfunktioner. För att definiera en klass av funktionärer som använder denna uppsättning som domän bör vi vara säkra på att det faktiskt finns medlemmar i denna uppsättning., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

definitionen
från denna punkt är definitionen av en distribution enkel. En distribution är en linjär funktionell
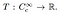
det vill säga, det är en kartläggning från uppsättningen testfunktioner till ett verkligt antal. – herr talman! Analogt med hur en specifik funktion fungerar på ett ingångsnummer och producerar en utgång, definieras specifika fördelningar av hur de omvandlar testfunktioner till siffror., Fördelningen av testfunktion φ kan skrivas som t (φ), eller vanligen som t,φ.
man kan nu se varför distributioner kallas generaliserade funktioner. För någon
klassisk funktion som integrerad

är väl definierat, och det finns en motsvarande fördelning F sådan att 〈F,φ〉ger värdet av denna integral., Det finns dock också fördelningar som inte motsvarar klassiska funktioner; fördelningar är mer allmänna. Som det borde vara tydligt nu är det kanoniska exemplet på en fördelning som inte motsvarar en klassisk funktion Dirac δ., Vi kommer därför äntligen fram till en fullständigt rigorös definition av δ Som distributionen så att

det generaliserade eller ”svaga” derivatet
δ-distributionen är bara en av oändligt många distributioner som inte
motsvarar klassiska funktioner. Vi kan få lite mer av dessa genom att differentiera δ i fördelningens mening., Men hur löser begreppet
distribution problemet med differentiering som diskuterats tidigare? Vi behöver bara generalisera begreppet differentiering som gäller för distributioner.
överväg en funktion f, f, C1, så att den kontinuerligt kan differentieras. Beräkning med hjälp av integration av delar ser vi att

termen inom parentes försvinner eftersom φ, som testfunktion, har kompakt stöd., Detta generaliserar till en distribution, säg F’, som motsvarar funktionen f’:

denna beräkning generaliserar ganska lätt till fördelningar som inte motsvarar en klassisk funktion f., På så sätt kan vi definiera derivatet T’ av T i betydelsen för distributioner:

detta kallas också ibland det svaga derivatet, eftersom det utökar derivat till funktioner som normalt inte skulle vara differentierbara. Detta generaliserar ännu längre, till högre orderderivat., Vi kan definiera nth-derivatet av en distribution t som t, där den senare är distributionen så att

Här,
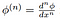
är det klassiska derivatet av testfunktionen, som garanteras
att existera genom själva definitionen av testfunktioner!, Av detta följer att alla fördelningar är oändligt differentierbara (i fördelningens mening).
detta tar bort helt den kamp som Dirac och andra mötte när man differentierade δ-funktionen. Med vad vi har definierat här siktar ett derivat av δ helt enkelt för värdet av ett annat funktionsderivat vid noll., Formellt

ök upp i litteraturen långt innan denna teori kom till existens.
det finns ett antal andra operationer som gäller för funktioner som har generaliserats för att gälla för distributioner. De kan läggas till och subtraheras, convolved och transformeras med Laplace och Fourier Transformer., Det är emellertid omöjligt att definiera multiplikationen av fördelningar på ett sätt som bevarar algebra som gäller för klassiska funktioner (Schwartz omöjlighet teorem).