När en ”normal” fraktion innehåller fraktioner i täljaren eller nämnaren eller båda, anser vi att det är en komplex fraktion. Denna typ av fraktion är också känd som en sammansatt fraktion.
det finns två metoder som används för att förenkla sådan typ av fraktion.
Metod 1
viktiga steg:
- skapa en enda fraktion i täljaren och nämnaren.,
- tillämpa delningsregeln för fraktioner genom att multiplicera täljaren med den ömsesidiga eller inverse av nämnaren.
- förenkla, om det behövs.
Metod 2
viktiga steg:
- hitta den minst gemensamma nämnaren (LCD) av alla nämnare i de komplexa fraktionerna.
- multiplicera denna LCD till täljaren och nämnaren för den komplexa fraktionen.
- förenkla, om det behövs.,
Efter att ha gått igenom några exempel, bör du inse att Metod 2 är mycket bättre än Metod 1 eftersom det nästan alltid tar färre steg för att komma till det slutliga svaret.
exempel på hur man förenklar komplexa fraktioner
exempel 1: förenkla den komplexa fraktionen nedan.
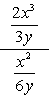
- med Metod 1
både täljaren och nämnaren för den komplexa fraktionen uttrycks redan som enstaka fraktioner. Det här är toppen!,

nästa steg är att tillämpa delningsregeln genom att multiplicera täljaren med den ömsesidiga nämnaren. Avsluta genom att avbryta vanliga faktorer för att få det slutliga svaret.
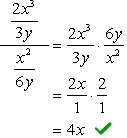
- använda Metod 2
hitta LCD-skärmen för hela problemet, det vill säga LCD-skärmen för de övre och nedre valörerna.,

eftersom LCD-skärmen på 3Y och 6y är just \textbf{6y}, kommer vi nu att multiplicera den komplexa täljaren och nämnaren med den här LCD-skärmen. Efter det kan vi förvänta oss att problemet reduceras till en enda bråkdel som kan förenklas som vanligt.
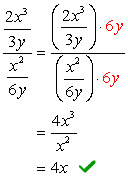
exempel 2: förenkla den komplexa fraktionen nedan.,
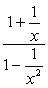
- använda Metod 1
i den här metoden vill vi skapa en enda fraktion både i täljaren och nämnaren. Självklart skulle detta problem kräva att vi gör det först innan vi utför division.
Lägg till fraktionerna i täljaren och subtrahera dem i nämnaren.,
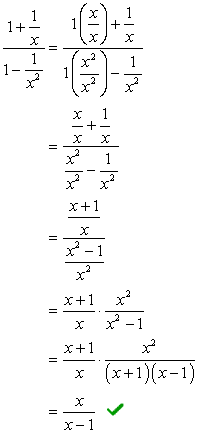
- använda Metod 2
titta på nämnarna \large{x} och \large{x^2}, dess LCD måste vara \large{x^2} multiplicera toppen och botten med denna LCD.
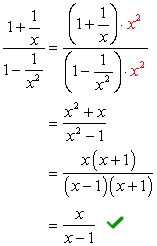
exempel 3: förenkla den komplexa fraktionen nedan.,
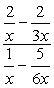
- använda Metod 1
Skapa enstaka fraktioner i både täljaren och nämnaren, följ sedan genom att dividera fraktionerna.
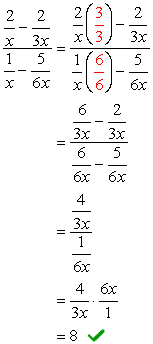
- använda Metod 2
den övergripande LCD-skärmen för nämnarna är \color{red}6x. använd detta för att multiplicera genom de övre och nedre uttrycken.,
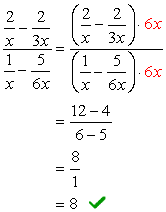
exempel 4: förenkla den komplexa fraktionen nedan.
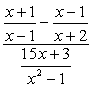
För det här problemet kommer vi endast att använda Metod 1.
problemet kräver att du använder FOLIEMETODEN (multiplikation av två binomialer) och en enkel faktorisering av trinomial. Det kan se lite skrämmande först; men om du uppmärksammar detaljer, garanterar jag dig att det inte är så illa.,
om du observerar är den komplexa nämnaren redan i den form som vi vill ha – med en fraktionssymbol. Det betyder att vi måste arbeta lite på den komplexa täljaren. Vårt nästa steg skulle vara att omvandla den komplexa täljaren till en” enkel ” eller enkel fraktion.
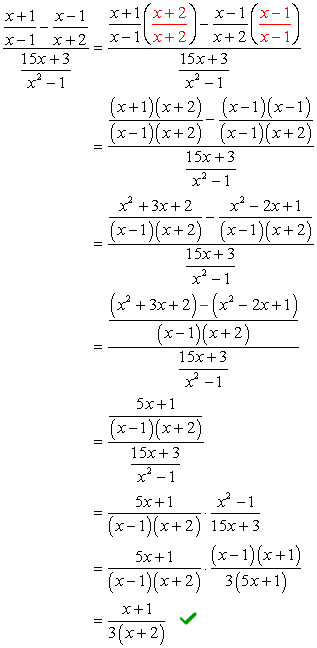
exempel 5: förenkla den komplexa fraktionen nedan.
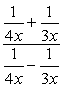
För det här problemet kommer vi endast att använda Metod 2.,
Observera att LCD-skärmen för alla nämnare är just \ color{red}12x. Använd detta som den gemensamma multiplikatorn för både övre och nedre uttryck.
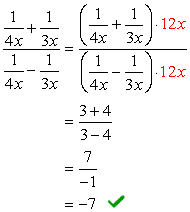
öva med kalkylblad
Du kan också vara intresserad av:
multiplicera komplexa fraktioner
dividera komplexa tal