
för elektromagnetism allt du behöver veta är vad som händer när du har + eller – avgifter, vad som händer när de kommer nära och vad som händer när de rör sig. Nu räcker det! För alla icke-quantum EM finns det bara 5 formler du behöver.,Lorentz ekvation beskriver all el, magnetism, ljus, ljud, strålning, faktiskt de flesta av fysik:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
hur illa kan ett ämne vara om du kan beskriva allt med bara 5 ekvationer, kan du förmodligen passa dem alla på baksidan av en beermat., Nu när du har sett slutsatsen kan vi gå till början och läsa hela historien i detalj. Om du inte gör en universitetskurs kan du komma undan med att inte veta exakt vad ekvationen betyder eller gör, men den här webbplatsen kommer att förklara dem senare, först kan du komma tillbaka till grunderna.
grunderna
laddningen kommer i 2 typer, positiva och negativa och mäts i Coulombs (C). Om du har en avgift på egen hand det avger ett fält i alla riktningar. Fältet från en avgift representeras av E som i e-föreläsning., Om du lägger en annan laddning i fältet upplever det en kraft. Som avgifter avvärja och till skillnad från avgifter locka. Ju större laddning desto starkare kraft och ju längre bort avgifterna desto svagare kraft, exakt vad du förväntar dig. Detta förhållande kan representeras av Coulombs lag;
![]()
och
![]()
![]() ’s är de två laddningar och
’s är de två laddningar och ![]() är avståndet mellan dem kvadrat., Den andra biten är bara en konstant som ungefär motsvarar 9000000000. (Den exakta härledningen av denna lag finns här). Från dessa kan du se att kraften bara är fälttiderna av vilken laddning du lägger in,
är avståndet mellan dem kvadrat., Den andra biten är bara en konstant som ungefär motsvarar 9000000000. (Den exakta härledningen av denna lag finns här). Från dessa kan du se att kraften bara är fälttiderna av vilken laddning du lägger in, ![]() . Med hjälp av detta kan du träna fältet eller kraften mellan partiklar eller atomer eller något med laddning förutsatt att de inte rör sig. När du börjar en avgift flytta andra saker hända.
. Med hjälp av detta kan du träna fältet eller kraften mellan partiklar eller atomer eller något med laddning förutsatt att de inte rör sig. När du börjar en avgift flytta andra saker hända.
saker som rör sig
så snart en laddning börjar röra sig ger den ett annat fält., Det nya fältet är magnetism och representeras av B som i b-magmatism?
anledningen till att det är B är helt enkelt att det var det andra i en alfabetisk lista:
- elektromagnetisk vektorpotential: a
- magnetisk induktion: B
- Total elektrisk ström: c
- elektrisk förskjutning: d
- elektromotorisk kraft: e
- mekanisk kraft: F
- hastighet vid en punkt: g
- magnetisk intensitet: h
(detta förklarar också var h kommer ifrån för dem som är intresserade).,
så nu din partikel eller atom eller vad har 2 fält kommer ut. Den fullständiga ekvationen för att beskriva hur båda fälten verkar på en partikel är
![]()
som kallas Lorentz-kraften. Symbolen![]() betyder inte multiplikation, i det här sammanhanget betyder det Cross-Product. Det är i grunden ett kort sätt att skriva ”
betyder inte multiplikation, i det här sammanhanget betyder det Cross-Product. Det är i grunden ett kort sätt att skriva ”![]() gånger
gånger![]() gånger sinus för vinkeln mellan”., Detta beror på att fältet
gånger sinus för vinkeln mellan”., Detta beror på att fältet![]() skjuter vid 90° till vilken någonsin riktning den pekar och vilken riktning du rör dig i. Nu om du inte gör EM förbi A-nivå kan du glömma alla riktningar och vinklar och bara skriva
skjuter vid 90° till vilken någonsin riktning den pekar och vilken riktning du rör dig i. Nu om du inte gör EM förbi A-nivå kan du glömma alla riktningar och vinklar och bara skriva
![]()
om vi utökar ovanstående uttryck har vi
![]()
men vi kan redan en av dessa bitar, ![]() är bara Coulombs lag., Också, på A-nivå eller under situationen kommer förmodligen att förenklas så du behöver bara överväga
är bara Coulombs lag., Också, på A-nivå eller under situationen kommer förmodligen att förenklas så du behöver bara överväga ![]() och
och ![]() fält separat., Så du kommer förmodligen bara att behöva använda en av följande två formler,
fält separat., Så du kommer förmodligen bara att behöva använda en av följande två formler,
![]()
![]()
självklart ![]() är kraften och
är kraften och
är laddning,![]() och
och![]() är de två fält som tidigare beskrivits och
är de två fält som tidigare beskrivits och![]() är hastigheten för den rörliga laddningen., Det elektriska fältet mäts i SI-enheterna i Newtons per coulomb (
är hastigheten för den rörliga laddningen., Det elektriska fältet mäts i SI-enheterna i Newtons per coulomb (![]() ) eller, likvärdigt, volt per meter (
) eller, likvärdigt, volt per meter (![]() ). Det magnetiska fältet har SI-enheter av Teslas (T), motsvarande Webers per kvadratmeter (
). Det magnetiska fältet har SI-enheter av Teslas (T), motsvarande Webers per kvadratmeter (![]() ) eller volt sekunder per kvadratmeter (
) eller volt sekunder per kvadratmeter (![]() )
)
Kretsar
Nu är jag inte en stor fan av kretsar, aldrig har varit, nu förhoppningsvis kommer jag vara professionell nog att mitt ogillande av dem kommer inte komma över i det här avsnittet, men om den gör det jag ber om ursäkt i förväg., Om jag verkligen börjar kämpa med mitt hat kan jag behöva ringa in en andra författare
a kretsar är i grunden bara en serie rörliga avgifter med enstaka objekt eller enhet på det sätt som påverkar flödet. Nu när jag säger elektronerna rör sig runt de flesta människor kommer att tro att deras fortkörning runt på nära ljusets hastighet, men detta är fel. De faktiska elektronerna rör sig extremt långsamt, det är den våg som färdas snabbt. Som nämnts ovan som avgifter avvärja, så sätta en elektron bredvid en annan och de kommer att röra sig isär., Med en ström i en tråd har du i princip ett rör av elektroner och du lägger till en till en av ändarna, vilket gör att nästa elektron flyttar ner vilket i sin tur drev nästa och så vidare. Så du har en mexikansk vågliknande effekt som rör sig snabbt, men elektronerna själva rör sig bara långsamt.
kretsar innehåller vanligtvis alla typer av olika objekt och enheter beroende på vad de är för, och beroende på hur du ställer in dem alla i kretsen beror på hur du gör alla er beräkningar.
vilket är vilket?,
om du konfigurerar all din komponent i en sluten slinga som så

då säger vi att alla komponenter är i Serie. Om du ställer in dem med förgreningsvägar som så

då säger vi att komponenterna är parallella. Du kan också göra kretsar som är en blandning av serier och parallella avsnitt som så

ampere, volt och Ohm (Oh my!,)
vi kallar de rörliga laddningarna en ström, och den mäts i SI-enheten för Amps (a). Amps motsvarar den mängd laddning som passerat under en viss tid, så 2 coulombs på 6 sekunder kommer att motsvara 0,3 A. detta, som de flesta saker i fysik kan uttryckas i en fin formel för dig att lära dig
![]()
en annan viktig idé i kretsar är spänning eller potentiell skillnad. Volt är i grunden skillnaden i den elektriska potentialen vid två olika punkter., Den elektriska potentialen mellan 2 poäng ges som
![]()
där ![]() är avståndet mellan
är avståndet mellan ![]() och
och ![]() . Det är i princip fälttider avstånd.
. Det är i princip fälttider avstånd.
en annan viktig idé när det gäller kretsar är motstånd. Motstånd är i grunden ett mått på hur mycket motstånd motsätter sig en elektrisk ström., Nästan alla objekt eller enheter i en krets orsakar motstånd och att beräkna det totala motståndet i en krets som du använder en eller flera av dessa regler
![]()
![]()
en av de viktigaste och grundläggande ekvationerna i kretsar är Ohms lag, och det gäller ström, spänning och motstånd.
![]()
den djupa änden
det här är det. Klassisk EM går inte djupare än detta., Dessa 4 är den grundläggande ekvationen för alla fält i EM. De kan ta lite att få huvudet runt men när du gör det bör alla vettigt, typ av.,
![]()
![]()
![]()
![]()
om du inte vet om integration och differentiering föreslår jag att du går över till integrationssektionen eller differentieringssektionen, jag ska försöka förklara det här men jag kommer huvudsakligen att fokusera på fysiken.
Gauss’ lag
Ok sedan först upp har vi Gauss’ lag.,
![]()
detta säger att integralet av det elektriska fältet, ![]() , genom ett stängt område
, genom ett stängt område ![]() är lika med den totala laddningen inuti området,
är lika med den totala laddningen inuti området, ![]() dividerat med
dividerat med ![]() .
. ![]() är en konstant som kallas permittiviteten för ledigt utrymme och dyker upp över hela fysiken tillsammans med
är en konstant som kallas permittiviteten för ledigt utrymme och dyker upp över hela fysiken tillsammans med![]() vilket är permeabiliteten för ledigt utrymme., Vad denna ekvation betyder är att du kan ta vilken sluten yta du vill och hitta fältet
vilket är permeabiliteten för ledigt utrymme., Vad denna ekvation betyder är att du kan ta vilken sluten yta du vill och hitta fältet![]() som går igenom, förutsatt att du kan göra matematiken. Vanligtvis kan du inte. men det finns ett antal fall när det är trevligt och enkelt. Fall då fältet
som går igenom, förutsatt att du kan göra matematiken. Vanligtvis kan du inte. men det finns ett antal fall när det är trevligt och enkelt. Fall då fältet![]() kommer rakt ut genom ytan jämnt., Fallen är
kommer rakt ut genom ytan jämnt., Fallen är
- en sfärisk yta runt en punkt eller sfär
- en cylindrisk yta runt en oändlig tråd
- en vanlig yta över en del av ett oändligt plan
jag erkänner dessa ljud vaga och abstrakta så jag kommer att visa med hjälp av ett diagram.



det här är de gaussiska ytorna., I grund och botten med dessa ytor allt du försöker göra är att göra livet enklare. Du ser bara till att ytan alltid är samma avstånd från laddningskällan och att fältet alltid går igenom vid 90 grader. Du kan sedan träna integralet med dina ögon stängda så lätt. Den vänstra sidan av Gauss lag blir e gånger ytan av den form du valde.
- en sfärisk yta blir
 , där
, där är sfärens radie.,
är sfärens radie., - en cylindrisk yta blir
 , där
, där  och
och  är cylinderns längd och radie.
är cylinderns längd och radie. - en vanlig yta blir
 , där
, där är området ovanför och under den oändliga ytan (du behöver faktorn 2 eftersom fältet går över och under ytan vid 90 grader).,
är området ovanför och under den oändliga ytan (du behöver faktorn 2 eftersom fältet går över och under ytan vid 90 grader).,
So Gauss’ law for a sphere becomes
![]()
![]()
![]()
Which was introduces earlier as Coulombs Law, now you know where it came from., Gauss’ lag för en oändlig laddningslinje är bara
![]()
![]()
![]()
nu i detta något nytt har införts, ![]() . Om du har en oändlig laddningslinje är den totala laddningen på den oändlig och det finns inget sätt att veta hur mycket av den oändliga laddningen du skulle ha inuti din gaussiska yta., Det är där
. Om du har en oändlig laddningslinje är den totala laddningen på den oändlig och det finns inget sätt att veta hur mycket av den oändliga laddningen du skulle ha inuti din gaussiska yta., Det är där ![]() kommer in, det är ett värde av laddning per enhetslängd, så om
kommer in, det är ett värde av laddning per enhetslängd, så om ![]() =4Cm
=4Cm![]() och du har 5 meter sedan laddningen
och du har 5 meter sedan laddningen ![]() är bara 20C. det är allt
är bara 20C. det är allt ![]()
för en oändlig yta gauss’ lag blir
![]()
återigen en ny symbol har lagts till men dess precis som den tidigare., ![]() är bara avgiften per enhet område, så om
är bara avgiften per enhet område, så om![]() =5Cm
=5Cm![]() och du har en 100m
och du har en 100m![]() område den totala avgiften är 500C.
område den totala avgiften är 500C.
laddad Ring
låt oss säga att du har en laddad ring och du behöver veta fältet som produceras från det. Återigen kommer vi att använda ett av de viktigaste verktygen i fysiken, vilket gör saker enklare. För det första tittar vi bara på fältet längs ringens axel, annars blir det bara för komplicerat och det är inte värt ansträngningen., Nu kan vi bara ta en mycket liten del av ringen och säga att det är en sfär. Det här är inte riktigt sant, men ju mindre vi gör avsnittet desto mer kan vi få det att likna en punktladdning. Så du har något liknande
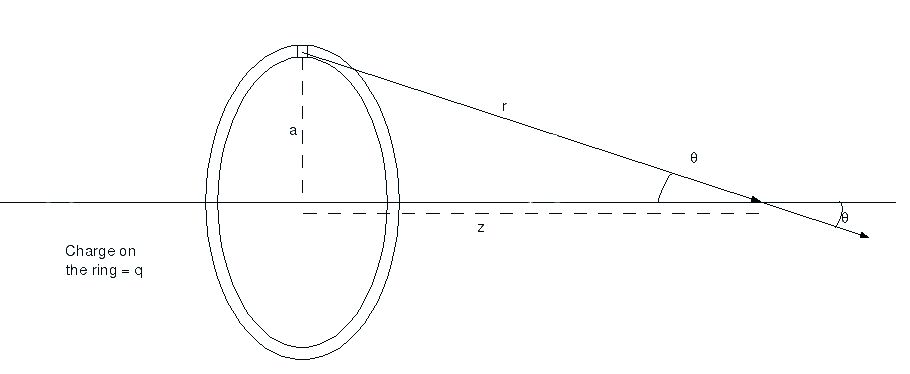
du vill hitta fältet vid en punkt ![]() längs axeln från ringen av total laddning
längs axeln från ringen av total laddning ![]() och radie
och radie ![]() och radie . Den lilla kvadratiska delen högst upp, det är den bit som du antar är en laddad sfär., Nu vet vi inte hur mycket laddning som finns i den lilla sektionen eftersom du kan göra den vilken storlek du vill så vi kallar bara laddningen
och radie . Den lilla kvadratiska delen högst upp, det är den bit som du antar är en laddad sfär., Nu vet vi inte hur mycket laddning som finns i den lilla sektionen eftersom du kan göra den vilken storlek du vill så vi kallar bara laddningen ![]() , en liten mängd
, en liten mängd ![]() . Så vi har nu
. Så vi har nu
![]()
nu om du tänker på det, kommer varje bit av ringen ovanför axeln som trycker ner att ha en lika stor bit under axeln som skjuter upp. Det kommer också att vara samma för vänster och höger och alla andra delar av ringen., Så all kraft från ringen kommer bara att fungera längs axeln. För att bara träna denna bit behöver vi använda lite trig. Vi måste gånger fältet med ![]() för att få den axiella komponenten.,
för att få den axiella komponenten.,
![]()
As you may or may not know ![]() can also be described (using SOH CAH TOA) by the following relationship for our situation
can also be described (using SOH CAH TOA) by the following relationship for our situation
![]()
As ![]() is the adjacent side and
is the adjacent side and ![]() is the hypotenuse., Så nu har vi
is the hypotenuse., Så nu har vi
![]()
men vi kanske inte vet vad ![]() är. Vi vet radien på disken,
är. Vi vet radien på disken, ![]() , och avståndet vi är från disken,
, och avståndet vi är från disken, ![]() .,
.,
![]()
nu vill vi bli av med det ![]() , så vi integrerar
, så vi integrerar
![]()
nu vet vi från diagrammet i början att den totala laddningen på disken är ![]() , så om vi lägger till alla små bitar av
, så om vi lägger till alla små bitar av ![]() summan ska vara
summan ska vara ![]() , så integralet är bara
, så integralet är bara ![]() .,
.,
![]()
så där har du det, ![]() fält från en laddad disk. Allt du behöver är fältet från en punkt och lite trig kunskap och du kan räkna ut det. Jag kunde bara ha gett dig den slutliga lösningen, men på så sätt kan du se var den kom ifrån och sedan om du glömmer det kan du kanske räkna ut det från första principer som ovan.,
fält från en laddad disk. Allt du behöver är fältet från en punkt och lite trig kunskap och du kan räkna ut det. Jag kunde bara ha gett dig den slutliga lösningen, men på så sätt kan du se var den kom ifrån och sedan om du glömmer det kan du kanske räkna ut det från första principer som ovan.,
Gauss’ lag för Magnetism
det här är trevligt och enkelt men har några stora konsekvenser. Gauss’ lag för Magnetism är
![]()
dess like the ordinary gauss’ law in that it describes a field, this time its the magnetic field, ![]() . Det står att integralet av B över en sluten yta,
. Det står att integralet av B över en sluten yta,![]() är noll. Ingenting. Varje fältlinje som går ut ur ytan har en ekvivalent som går in. Det finns inget övergripande fält., Detta innebär att det är omöjligt att få källor till magnetfält. Medan elektroner och protoner är fältets ursprung, från vilka fältlinjer avviker från eller konvergerar till, finns det ingen magnetisk analog. Magnetfältlinjer är alltid slutna slingor, ingen start, ingen ände. Detta har naturligtvis inte hindrat människor från att förbereda om vi hittar en magnetisk monopol.
är noll. Ingenting. Varje fältlinje som går ut ur ytan har en ekvivalent som går in. Det finns inget övergripande fält., Detta innebär att det är omöjligt att få källor till magnetfält. Medan elektroner och protoner är fältets ursprung, från vilka fältlinjer avviker från eller konvergerar till, finns det ingen magnetisk analog. Magnetfältlinjer är alltid slutna slingor, ingen start, ingen ände. Detta har naturligtvis inte hindrat människor från att förbereda om vi hittar en magnetisk monopol.
denna ekvation kan tyckas trevlig, och det är, men det är helt värdelös på egen hand., Vanligtvis är ett 0-resultat i fysiken ganska viktigt, det betyder att något speciellt kan hända, här visar det att magnetiska monopoler inte existerar.
Faradays lag
nu blir det mer komplext, Här har vi Faradays lag,
![]()
jag ska gå igenom varje bit för att visa dig vad det faktiskt betyder. Först har vi vänster sida som är lätt. Det är precis som Gauss lag bara integralet är över en annan sak., Istället för att hitta den totala![]() fältet genom en yta,
fältet genom en yta,![]() , vi nu hitta den totala
, vi nu hitta den totala![]() fältet runt en sluten slinga
fältet runt en sluten slinga![]() . Det är allt som är annorlunda med vänster sida, inga fler ytor, bara slutna slingor. Nu till höger. Först upp har vi en minus, notera komplicerat om det. Varför dess det kommer att förklaras senare. Nästa har vi en annan integrerad, och den här ser hemsk ut. Symbolen
. Det är allt som är annorlunda med vänster sida, inga fler ytor, bara slutna slingor. Nu till höger. Först upp har vi en minus, notera komplicerat om det. Varför dess det kommer att förklaras senare. Nästa har vi en annan integrerad, och den här ser hemsk ut. Symbolen![]() betyder i princip en liten förändring., Så
betyder i princip en liten förändring., Så ![]() är en förändring i
är en förändring i![]() , och
, och![]() är en förändring i
är en förändring i![]() , där
, där![]() är dags. Hela
är dags. Hela![]() är förändringstakten för
är förändringstakten för![]() , dess hur mycket
, dess hur mycket![]() ändras (
ändras (![]() ) under en viss tid (
) under en viss tid (![]() ). Och det integreras över ett område
). Och det integreras över ett område ![]() .,
., ![]() är området inuti den slutna slingan
är området inuti den slutna slingan![]() , om du ritar någon slumpmässig squiggly sak att se till att linjen inte korsar sig själv och att den ansluter sig då längden runt linjen är din
, om du ritar någon slumpmässig squiggly sak att se till att linjen inte korsar sig själv och att den ansluter sig då längden runt linjen är din![]() och området inuti linjen är din
och området inuti linjen är din![]() . Enkelt ja? Så den totala
. Enkelt ja? Så den totala ![]() runt en slinga är precis lika med minus av den förändrade
runt en slinga är precis lika med minus av den förändrade![]() genom slingan.
genom slingan.
vad händer om det inte finns någon![]() ?, Jo det finns ingen
?, Jo det finns ingen![]() så
så![]() är noll, vilket gör integral 0, så ingen
är noll, vilket gör integral 0, så ingen![]() . Vad händer om du har en konstant
. Vad händer om du har en konstant ![]() ? Väl igen
? Väl igen ![]() är 0. Så
är 0. Så![]() är noll, vilket gör integralet 0, så igen ingen
är noll, vilket gör integralet 0, så igen ingen![]() . Du kan bara inducera ett
. Du kan bara inducera ett![]() – fält från ett
– fält från ett![]() – fält.,
– fält.,
betydelsen av minustecknet kommer från det faktum att![]() fält skapar
fält skapar![]() fält och
fält och![]() fält skapar
fält skapar![]() fält (som visas i Faradays och Amperes lagar). Om minusen inte var där skulle fälten bara fortsätta bygga och bygga så småningom ge oändlig energi, och det är inte tillåtet!
fält (som visas i Faradays och Amperes lagar). Om minusen inte var där skulle fälten bara fortsätta bygga och bygga så småningom ge oändlig energi, och det är inte tillåtet!
Ampère-Maxwell Law
den sista av Maxwells ekvationer är Ampere-Maxwell law., Precis som de två första lagarna var liknande så är de två sista, det finns ett mönster för dem i denna ordning som kan göra dem lättare att komma ihåg. ![]() över ett område,
över ett område, ![]() över ett område,
över ett område, ![]() runt en slinga och nu äntligen
runt en slinga och nu äntligen ![]() runt en slinga. Ekvationen är
runt en slinga. Ekvationen är
![]()
vänster sida, enkel, integrerad av B runt en sluten slinga. Höger sida, inte så lätt., Låt oss först ignorera![]() bit, jag kommer tillbaka till det. Annat än
bit, jag kommer tillbaka till det. Annat än![]() , dess mycket lik Faradays lag. Du har ett annat ändringsfält integrerat över ett område, men den här gången dess
, dess mycket lik Faradays lag. Du har ett annat ändringsfält integrerat över ett område, men den här gången dess ![]() . Den här gången men istället för att multiplicera med minus 1 multiplicerar du med
. Den här gången men istället för att multiplicera med minus 1 multiplicerar du med ![]() . Återigen är dessa två mycket viktiga värden i fysiken, ensamma och kombinerade. De är i hjärtat av EM., Så ditt magnetfält runt en slinga är precis lika med det förändrade e-fältet som går igenom det gånger av
. Återigen är dessa två mycket viktiga värden i fysiken, ensamma och kombinerade. De är i hjärtat av EM., Så ditt magnetfält runt en slinga är precis lika med det förändrade e-fältet som går igenom det gånger av ![]() , men då måste du lägga till lite. Detta är
, men då måste du lägga till lite. Detta är ![]() – biten. Det här är bara den nuvarande som går runt looptiderna med
– biten. Det här är bara den nuvarande som går runt looptiderna med ![]() , det beror på att, som sagt i saker som rör sig, om du har en rörlig laddning, dvs en ström, får du ett magnetfält. Så du måste lägga ihop de två bitarna. Så där, klart.,
, det beror på att, som sagt i saker som rör sig, om du har en rörlig laddning, dvs en ström, får du ett magnetfält. Så du måste lägga ihop de två bitarna. Så där, klart.,
en annan form av den djupa änden
samt skriva Maxwells ekvationer ovan, i vad som kallas integrerad form, kan du också skriva dem i differentiell form som så
![]()
![]()
![]()
![]()
ännu en form av den djupa änden
skriva Maxwells ekvationer i en av ovanstående två former är verkligen en förenkling., Både integralformen och differentialformen är vektorekvationer och de sparar dig att skriva ut de fullständiga 8 Maxwell-ekvationerna för fälten ![]() och
och ![]() I alla tre dimensionerna.,div id=”a2ea6619e6″>
I alla tre dimensionerna.,div id=”a2ea6619e6″>
![]()
![]()
![]()
Well iot turns out you can also compactify the four vector Maxwell equations into two tensor equations like so
![]()
![]()
Here ![]() is a vector with four components, sometimes called the 4-current, and
is a vector with four components, sometimes called the 4-current, and ![]() is a 4×4 matrix called the electromagnetic tensor., De definieras som
is a 4×4 matrix called the electromagnetic tensor., De definieras som
(6) 
(7) 
där ![]() är ljusets hastighet. Den
är ljusets hastighet. Den![]() och
och![]() bara berätta var i vektorn eller matrisen att titta, men förvirrande för någon start på 0, så
bara berätta var i vektorn eller matrisen att titta, men förvirrande för någon start på 0, så![]() och
och![]() (inte att förväxla med
(inte att förväxla med![]() kubik). Samma med
kubik). Samma med ![]() , så
, så ![]() och
och ![]()