icosahedron (Svenska)

den vanliga icosahedron är en av de fem platoniska fasta ämnena. Det är en konvex regelbunden polyhedron bestående av tjugo triangulära ansikten, med fem möte vid var och en av de tolv hörn. Den har 30 kanter och 12 hörn. Dess dubbla polyhedron är dodecahedron.,

mått

om kantlängden för en vanlig icosahedron är är radien för en avgränsad sfär (en som berör icosahedron vid alla hörn)

och radien för en inskriven sfär (tangent till var och en av icosahedron ansikten)

medan midradius , som berör mitten av varje kant, är

där 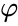(även kallad ) är det gyllene förhållandet.,

område och volym

ytan och volymen av en vanlig icosahedron med kantlängd är:

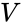
kartesiska koordinater

följande kartesiska koordinater definierar hörn av en icosahedron med kantlängd 2, centrerad vid ursprunget:

där är det gyllene förhållandet (även skrivet τ)., Observera att dessa hörn bildar fem uppsättningar av tre ömsesidigt centrerade, ömsesidigt ortogonala gyllene rektanglar.

de 12 kanterna på en vanlig oktaedron kan delas upp i det gyllene förhållandet så att de resulterande hörnen definierar en vanlig icosahedron. Detta görs genom att först placera vektorer längs oktahedronens kanter så att varje ansikte begränsas av en cykel, sedan på samma sätt partitionera varje kant i det gyllene medelvärdet längs riktningen av dess vektor., De fem oktahedra som definierar någon given icosahedron bildar en vanlig polyhedral förening, liksom de två icosahedra som kan definieras på detta sätt från någon given oktahedron.

Konstruktion genom ett system av ekviangulära linjer

följande konstruktion av icoshaedron undviker tråkiga beräkningar i nummerfältet som är nödvändiga i mer elementära tillvägagångssätt.

förekomsten av icosahedron motsvarar förekomsten av sex ekviangulära linjer i ., Att korsa ett sådant system av ekviangulära linjer med en euklidisk sfär centrerad vid deras gemensamma korsning ger de tolv hörnen av en vanlig icosahedron som lätt kan kontrolleras. Omvänt, om man antar förekomsten av en vanlig icosahedron, bildar linjer som definieras av sina sex par motsatta hörn ett ekviangulärt system.

för att konstruera ett sådant equiangular system börjar vi med matrisen

med kvadratisk storlek ., (Mnemonic: matrisen kodar vinklarna, akuta för en positiv post, trubbig annars, mellan fem cykliskt på varandra följande hörn intill ett första vertex av en icosahedron centrerad vid ursprunget.)

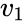
en enkel beräkning ger. Detta innebär att har egenvärden , båda med multiplicitet 3 eftersom är symmetrisk och spår 0., Matrisen inducerar thusan Euclidean struktur på kvoten utrymme som är isomorfisk till eftersom kärnan av har dimension 3. Bilden under projektionen av de sex koordinataxlarna I bildar således ett system med sex ekviangulära linjer i korsande parvis i en gemensam spetsig vinkel på ., Ortogonal projektion av på-eigenspace av ger således de tolv hörnen av icosahedron.

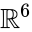
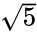
en andra enkel konstruktion av icosahedron använder representationsteori för den alternerande gruppen agerar genom direkta isometrier på icosahedron.

Stellationer

enligt specifika regler som definieras i boken femtionio icosahedra identifierades 59 stellationer för den vanliga icosahedron. Den första formen är icosahedronen själv., En är en vanlig Kepler-Poinsot solid. Tre är vanliga förening polyhedra.

21 av 59 stellationer

ytorna på icosahedron utsträckta utåt som plan skär, definiera regioner i rymden som visas av denna stellation av korsningar diagram i ett enda plan.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Dessa är invariant under samma rotationer som tetrahedron, och är något analoga med snub cube och snub dodecahedron, inklusive vissa former som är chiral och några med th-symmetri, dvs har olika symmetriplan från tetrahedron. Icosahedron har ett stort antal stellationer, inklusive en av Kepler-Poinsot polyhedra och några av de vanliga föreningarna, som kan diskuteras här.

icosahedron är unik bland de platoniska fasta ämnena i att ha en dihedral vinkel inte mindre än 120°. Dess dihedral vinkel är ungefär 138.19°.,ss än 120° och kan inte användas som står inför en regelbunden konvex polyeder eftersom en sådan konstruktion skulle inte uppfylla kravet på att minst tre ansikten möts vid en brytpunkt och lämnar en positiv avvikelse, vikbar i tre dimensioner, icosahedra kan inte användas som cellerna i en regelbunden konvex polychoron grund, på samma sätt, minst tre celler måste träffa på en kant och lämnar en positiv avvikelse, falsning i fyra dimensioner (i allmänhet för en konvex polytope i > mått, minst tre aspekter måste träffa på en topp och lämnar en positiv avvikelse, falsning i n-space)., Men i kombination med lämpliga celler med mindre dihedrala vinklar kan icosahedra användas som celler i semi-regelbunden polychora (till exempel snub 24-cell), precis som hexagoner kan användas som ansikten i semi-regelbunden polyhedra (till exempel den stympade icosahedron). Slutligen har icke-konvexa polytoper inte samma strikta krav som konvexa polytoper, och icosahedra är verkligen cellerna i icosahedral 120-cellen, en av de tio icke-konvexa regelbundna polychora.

en icosahedron kan också kallas en gyroelongerad femkantig bipyramid., Den kan sönderdelas i en gyroelongerad femkantig pyramid och en femkantig pyramid eller i en femkantig antiprism och två lika femkantiga pyramider.

icosahedron kan också kallas en snub tetrahedron, eftersom snubifiering av en vanlig tetrahedron ger en vanlig icosahedron., Alternativt, med hjälp av nomenklaturen för snub polyhedra som hänvisar till en snub kub som en snub cuboctahedron (cuboctahedron = rektifierad kub) och en snub dodecahedron som en snub icosidodecahedron (icosidodecahedron = rektifierad dodecahedron), kan man kalla icosahedron snub octahedron (oktahedron = rektifierad tetrahedron).

en rektifierad icosahedron bildar en icosidodekahedron.

icosahedron vs dodecahedron

När en icosahedron är inskriven i en sfär upptar den mindre av sfärens volym (60,54%) än en dodekahedron inskriven i samma sfär (66,49%).,

eftersom dessa är dualer är det också möjligt att omvandla den ena till den andra(se nedan).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	i vissa rollspel används den tjugosidiga munstycket (för kort, d20) för att bestämma framgång eller misslyckande av en åtgärd. Denna dö är i form av en vanlig icosahedron. Det kan numreras från” 0 ”till” 9 ” två gånger (i vilken form det vanligtvis fungerar som en tiosidig dö, eller d10), men de flesta moderna versioner är märkta från ”1” till ”20”. Se d20-systemet.,

en icosahedron är den tredimensionella spelplanen för Icosagame, tidigare känd som ICO Crystal Game.

en icosahedron används i brädspelet Scattergories att välja en bokstav i alfabetet. Sex små bokstäver, som X, Q och Z, utelämnas.

inuti en magisk 8-Ball, olika svar på Ja-Inga frågor skrivs ut på en vanlig icosahedron.

icosahedron visas i en funktionell form ses i Sol De La Flor ljus nyans., Rosetten som bildas av de överlappande bitarna visar likhet med Frangipani-blomman.

om varje kant av en icosahedron ersätts av ett ohm-motstånd, är motståndet mellan motsatta hörn 0,5 ohm och det mellan intilliggande hörn 11/30 ohm.

symmetrin gruppen av icosahedron är isomorf till den alternerande gruppen på fem bokstäver. Denna nonabelian enkla grupp är den enda icke-triviala normala undergruppen av den symmetriska gruppen på fem bokstäver., Eftersom Galois-gruppen i den allmänna kvintiska ekvationen är isomorf till den symmetriska gruppen på fem bokstäver, och det faktum att icosahedral-gruppen är enkel och nonabelian betyder att kvintiska ekvationer inte behöver ha en lösning i radikaler. Beviset på Abel-Ruffini teorem använder detta enkla faktum, och Felix Klein skrev en bok som utnyttjade teorin om icosahedrala symmetrier för att härleda en analytisk lösning på den allmänna kvintiska ekvationen.,

Se även

Mall:Wiktionarypar

• stympad icosahedron
• vanlig polyhedron
• geodetiska nät använd en iterativt bisekterad icosahedron för att generera nät på en sfär
• Jessens icosahedron

Mall:Wikisource1911Enc

Mall:commonscat

• weisstein, Eric W., ”icosahedron” från MathWorld.
• pappersmodeller av icosahedron
• den enhetliga Polyhedra
• K. J. M., MacLean, en geometrisk analys av de fem platoniska fasta ämnen och andra Semi-Regular Polyhedra
• interaktiv icosahedron modell – fungerar rätt i din webbläsare
• Virtual Reality Polyhedra Encyclopedia of Polyhedra
• Tulane.,edu är En diskussion av super struktur och ikosaeder
• Papper Modeller av Polyhedra Många länkar
• Origami Polyhedra – Modeller är tillverkade med en Modulär Origami
• video av hölje spegel är en skulptur

Mall:Polyhedra

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri jag rregulltsr:Икосаедарsv:Ikosaederta:utbröt முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.