introduktion till filosofi: logik

det finns en gammal uppfattning, som fortfarande hålls allmänt, att det som gör människor speciella-det som skiljer oss från ” fältets djur— – är att vi är rationella. Vad består rationalitet i? Det är en förargad fråga, men ett möjligt svar går ungefär så här: vi manifesterar vår rationalitet genom att engagera sig i aktiviteter som involverar resonemang—att göra anspråk och stödja dem med skäl, agera i enlighet med skäl och övertygelser, dra slutsatser från tillgängliga bevis och så vidare.,

denna resonemang aktivitet kan göras bra och det kan göras dåligt; det kan göras på rätt sätt eller felaktigt. Logik är den disciplin som syftar till att skilja bra resonemang från dåligt.

bra resonemang är inte nödvändigtvis effektivt resonemang. Som vi kommer att se i ett senare kapitel om logiska felaktigheter är dåliga resonemang genomgripande och ofta extremt effektiva—i den meningen att människor ofta övertalas av det. I logiken är godhetens standard inte effektivitet i övertygelse, utan snarare korrekthet enligt logiska regler.,

tänk till exempel Hitler. Han övertalade en hel nation att gå med på en mängd olika förslag som inte bara var falska men rent onda. Du kommer inte bli förvånad över att höra att om du undersöker det kritiskt, passerar hans resonemang inte logisk uppbåda. Hitlers argument var effektiva, men inte logiskt korrekta. Dessutom går hans övertygande tekniker utöver resonemang i betydelsen att säkerhetskopiera påståenden med skäl. Hitler förlitade sig på Hot, känslomässig manipulation, olämpliga påståenden etc. Det finns många retoriska knep man kan använda för att övertyga.,

i logiken studerar vi de regler och tekniker som gör det möjligt för oss att skilja bra, korrekt resonemang från dålig, felaktig resonemang.

eftersom det finns en mängd olika typer av resonemang och metoder för att utvärdera var och en av dessa typer, plus olika divergerande åsikter om vad som utgör korrekt resonemang, finns det många tillvägagångssätt för det logiska företaget. Vi talar om logik, men också om logiker. En logik är bara en uppsättning regler och tekniker för att skilja bra resonemang från dåligt., En logik måste formulera exakta standarder för att utvärdera resonemang och utveckla metoder för att tillämpa dessa standarder på vissa fall.

grundläggande begrepp

resonemang innebär påståenden eller uttalanden—göra dem och säkerhetskopiera dem med skäl, dra ut deras konsekvenser. Propositioner är de saker vi hävdar, staten, hävda.

propositioner är de typer av saker som kan vara sanna eller falska. De uttrycks av deklarativa meningar., Vi använder sådana meningar för att göra alla slags påståenden, från rutinmässiga fakta (”jorden kretsar kring solen”), till stora metafysiska avhandlingar (”verkligheten är en oföränderlig, funktionlös, enhetlig absolut”), till påståenden om moral (”det är fel att äta kött”).

det är viktigt att skilja meningar i deklarativ humör, som uttrycker propositioner, från meningar i andra stämningar, vilket inte gör det. Frågande meningar, till exempel, ställa frågor (”regnar det?”), och imperativa meningar utfärdar kommandon (”drick inte fotogen.”)., Det är ingen mening att fråga om dessa typer av meningar uttrycker sanningar eller falskhet, så de uttrycker inte propositioner.

vi skiljer också propositioner från de meningar som uttrycker dem, eftersom ett enda förslag kan uttryckas med olika meningar. ”Det regnar ”och” es regnet ” uttrycker båda påståendet att det regnar; en mening gör det på Engelska, den andra på tyska. ”John älskar Mary” och ”Mary är älskad av John” uttrycker båda samma proposition.

den grundläggande enheten för resonemang är argumentet., I logiken, med” argument ”menar vi inte en oenighet, en skrikande match; snarare definierar vi termen exakt:

Argument = en uppsättning förslag, varav slutsatsen är (tänkt att vara) stöds av de andra, lokalerna.

om vi resonerar genom att göra anspråk och säkerhetskopiera dem med skäl, är påståendet som backas upp slutsatsen av ett argument; de skäl som ges för att stödja det är argumentets lokaler., Om vi resonerar genom att dra en slutsats från en uppsättning uttalanden, är slutsatsen vi drar slutsatsen av ett argument, och uttalandena från vilka det dras är lokalerna.

Vi inkluderar den parentetiska Häcken – ”tänkt att vara” – i definitionen för att göra plats för dåliga argument. Ett dåligt argument, mycket grovt sett, är en där lokalerna misslyckas med att stödja slutsatsen; ett bra argument lokaler faktiskt stöder slutsatsen.

analys av argument

följande passage uttrycker ett argument:

så gör denna passage:

återigen är det ultimata syftet med logiken att utvärdera argument—för att skilja det goda från det dåliga. För att göra detta krävs distinktioner, definitioner, principer och tekniker som kommer att beskrivas i efterföljande kapitel. För tillfället kommer vi att fokusera på att identifiera och rekonstruera argument.

den första uppgiften är att förklara argument—att uttryckligen ange sina lokaler och slutsatser., Ett tydligt sätt att göra detta är helt enkelt att lista deklarativa meningar som uttrycker relevanta förslag, med en linje som skiljer lokalerna från slutsatsen, så:

1. McDonalds betalar sina arbetstagare mycket låga löner.
2. de djur som ger McDonalds kött höjs under beklagliga förhållanden.
3. McDonalds mat är mycket ohälsosamt.
4. / \därför bör du inte äta på McDonalds.

detta är en förklaring av den första argumentativa passagen ovan., För att identifiera slutsatsen av ett argument är det bra att fråga sig själv ,” Vad försöker den här personen att övertyga mig om att tro genom att säga dessa saker? Vad är den ultimata punkten i denna passage?”Svaret är ganska tydligt i det här fallet. En annan ledtråd om vad som händer i passagen tillhandahålls av ordet ” för ” i den tredje meningen. Tillsammans med andra ord, som ”sedan” och ”för”, indikerar det närvaron av en premiss. Vi kan kalla sådana ord premiss markörer. Symbolen ”/ trip ” kan läsas som stenografi för ”därför.,”Tillsammans med uttryck som ”följaktligen” ”således” ”följer det att” och ”vilket innebär att” ”därför” är en indikator som argumentets slutsats är på väg att följa. Vi kallar sådana locutions slutsats markörer. En sådan markör är inte närvarande i det första argumentet, men vi ser en i den andra, vilket kan förklaras sålunda:

1. universum är stort och komplext.
2. universum visar en häpnadsväckande grad av ordning.
3. planeterna kretsar runt solen enligt vanliga lagar.
4. djurs minutestdelar är ordnade exakt för att tjäna sina syften.,
5. sådan ordning och komplexitet kan inte uppstå slumpmässigt.
6. / \därför måste universum vara en produkt av en designer av enorm kraft och intellekt: Gud.

flera punkter i jämförelse med vår första förklaring är värda att notera här. Först, som nämnts, var vi varnade för slutsatsen av ordet ” därför.”För det andra krävde denna passage mycket mer omskrivning än den första. Den andra meningen är frågande, inte deklarativ, och så uttrycker den inte ett förslag., Eftersom argument per definition är samlingar av propositioner måste vi begränsa oss till deklarativa meningar när vi förklarar dem. Eftersom svaret på den andra meningen retorisk fråga är tydligt ”ja”, parafraserar vi som visas. Den tredje meningen uttrycker två propositioner, så i vår förklaring skiljer vi dem; var och en är en förutsättning.

så ibland, när vi förklarar ett argument, måste vi ta vad som finns i argumentativpassagen och ändra det något, så att alla meningar vi skriver ner uttrycker de förslag som finns i argumentet., Det här är parafrasering. Vid andra tillfällen måste vi göra ännu mer. Vi kan till exempel behöva införa förslag som inte uttryckligen nämns i argumentationspassagen, men som otvivelaktigt används i argumentets resonemang.

det finns ett grekiskt ord för argumenterande passager som lämnar vissa propositioner ostaterade: enthymemes. Här är ett exempel:

det finns en implicit premiss som lurar i bakgrunden här—något som inte har sagts, men som måste vara sant för argumentet att gå igenom. Vi behöver ett påstående som förbinder förutsättningen till slutsatsen—att överbrygga klyftan mellan dem. Något sådant: en allälskande Gud skulle inte tillåta oskyldiga människor att lida. Eller kanske: utbredd lidande är oförenligt med tanken på en allälskande gudom. Förutsättningen pekar på lidande, medan slutsatsen handlar om Gud; dessa propositioner förbinder dessa två påståenden., En fullständig förklaring av argumentativ passage skulle göra ett förslag som denna explicit:

1. många oskyldiga människor över hela världen lider.
2. en allälskande Gud skulle inte tillåta oskyldiga människor att lida.
3. / \därför kan det inte finnas en allälskande Gud.

detta är märket för de typer av tysta lokaler som vi vill avslöja: om de är falska undergräver de argumentet., Ofta är lokaler som detta ostaterade av en anledning: de är kontroversiella påståenden på egen hand, vilket kräver bevis för att stödja dem. så arguer lämnar dem ut och föredrar att inte fastna. När vi drar ut dem kan vi dock tvinga fram ett mer robust dialektiskt utbyte, med fokus på argumentet om kärnan i frågan. I det här fallet skulle en diskussion om Guds godhet och ondska i världen vara i ordning. Det finns mycket att säga om det ämnet., Filosofer och teologer har utvecklat utarbetade argument under århundradena för att försvara tanken att Guds godhet och mänskligt lidande är faktiskt kompatibla.

hittills har vår analys av argument inte varit särskilt djup. Vi har noterat vikten av att identifiera slutsatsen och tydligt ange lokalerna, men vi har inte tittat på hur uppsättningar av lokaler kan stödja deras slutsatser. Vi har bara noterat att lokalerna tillsammans ger stöd för slutsatser., Vi har inte tittat på hur de gör det, vilka slags relationer de har med varandra. Detta kräver djupare analys.

ofta kommer olika lokaler att stödja en slutsats—eller en annan premiss—individuellt, utan hjälp från någon annan. Tänk på detta enkla argument:

Propositioner 1 och 2 stöder slutsatsen, proposition 3—och de gör det självständigt. Var och en ger oss en anledning att tro att kriget var orättvist, och var och en står som en anledning även om vi skulle anta att den andra inte var sant; Detta är märket av oberoende lokaler.

det kan vara till hjälp, särskilt när argument är mer komplexa, att rita diagram som skildrar relationerna mellan lokaler och slutsats., Vi kan skildra argumentet ovan enligt följande:

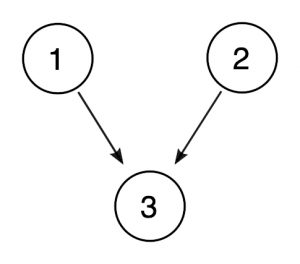
i ett sådant diagram representerar de cirklade numren propositionerna och pilarna representerar förhållandet mellan stöd från ett förslag till ett annat. Eftersom propositioner 1 och 2 varje stöd 3 självständigt, de får sina egna pilar.

andra relationer mellan lokaler är möjliga. Ibland ger lokalerna stöd till slutsatser endast indirekt, genom att ge oss en anledning att tro på någon annan premiss, som är mellanliggande mellan de två kraven., Tänk på följande argument:

i det här exemplet ger proposition 1 Stöd för proposition 2 (ordet ”därav” är en ledtråd), medan proposition 2 direkt stöder slutsatsen i 3., Vi skulle skildra relationerna mellan dessa propositioner således:

Ibland måste lokalerna arbeta tillsammans för att ge stöd till ett annat påstående, inte för att en av dem ger anledning att tro på den andra, men för att varken ger det stöd som behövs på egen hand; vi kallar sådana propositioner gemensamma lokaler. Tänk på följande:

i detta argument stöder varken premiss 1 eller Premiss 2 slutsatsen på egen hand. den andra förutsättningen är snarare en nyckel som låser upp slutsatsen från den villkorade premissen 1. Vi kan indikera ett sådant ömsesidigt beroende diagrammatiskt med parentes, så:

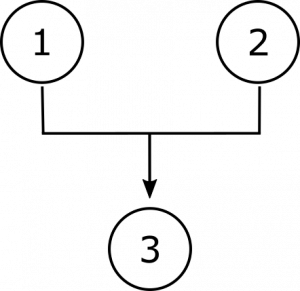
Schemaläggande argument på detta sätt kan vara till hjälp både för att förstå hur de fungerar och informera alla försök att kritiskt engagera sig med dem., Man kan tydligt se i det första argumentet att alla överväganden som framförs i strid med en av de oberoende lokalerna inte helt kommer att undergräva stödet för slutsatsen, eftersom det fortfarande finns en annan förutsättning för att ge det en viss grad av stöd. I det andra argumentet skulle dock skäl som talar mot den andra förutsättningen avskurna stödet för slutsatsen vid dess rot; och allt som strider mot den första förutsättningen kommer att lämna den andra i behov av stöd. Och i det tredje argumentet kommer överväganden som strider mot någon av de gemensamma lokalerna att undergräva stödet för slutsatsen., Särskilt när argument är mer komplexa kan sådana visuella hjälpmedel hjälpa oss att känna igen alla slutsatser som ingår i argumentet.

kanske kommer det att vara användbart att sluta med att överväga ett något mer komplext argument. Låt oss överväga vilken typ av nummer:

slutsatsen av detta argument är det sista förslaget, att siffrorna är abstrakta objekt. Observera att den första förutsättningen ger oss ett val mellan detta påstående och ett alternativ—att de är konkreta. Den andra förutsättningen förnekar det alternativet, och så arbetar lokaler 1 och 2 tillsammans för att stödja slutsatsen:

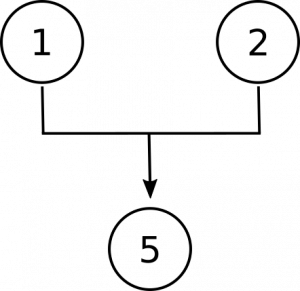
Nu måste vi göra plats i vårt diagram för propositioner 3 och 4. De är där för att ge oss skäl att tro att siffror inte är konkreta föremål., För det första, genom att hävda att siffrorna inte finns i rymden som konkreta objekt är, och för det andra genom att hävda att siffrorna inte interagerar med andra objekt, som konkreta objekt gör. Dessa är separata, oberoende skäl för att tro att de inte är konkreta, så vi slutar med det här diagrammet:

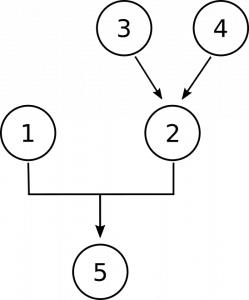
logik och filosofi

kärnan i det logiska företaget är en filosofisk fråga: Vad gör ett bra argument? Det vill säga, Vad är det för en uppsättning påståenden att ge stöd för något annat påstående? Eller kanske: när är vi berättigade att dra slutsatser?, För att svara på dessa frågor har logiker utvecklat en mängd olika logiska system som täcker olika typer av argument och tillämpar olika principer och tekniker. Många av de verktyg som utvecklats i logik kan tillämpas bortom filosofins gränser. Matematikern som bevisar en teorem, dataforskaren programmerar en dator, lingvisten som modellerar språkets struktur-alla dessa använder logiska metoder., Eftersom logiken har så bred tillämpning, och på grund av den formella/matematiska sofistikeringen av många logiska system, upptar den en unik plats i den filosofiska läroplanen. En klass i logik är vanligtvis till skillnad från andra filosofiklasser i att mycket lite tid spenderas direkt med och försöker svara på de ”stora frågorna”; snarare kommer en mycket snabbt ner till verksamheten att lära sig logiska formalismer. Frågorna logiken försöker svara på är viktiga filosofiska frågor, men de tekniker som utvecklats för att svara på dem är värda att studera på egen hand.,

detta betyder dock inte att vi bör tänka på logik och filosofi som bara tangentiellt relaterade; tvärtom är de djupt sammanflätade. För alla formella klockor och visselpipor som presenteras i det senaste avancerade logiska systemet är det längst ner en del av ett försök att svara på den grundläggande frågan om vad som följer av vad. Dessutom är logiken användbar för den praktiserande filosofen på minst tre andra sätt.

filosofer försöker svara på djupa, irriterande frågor—om verklighetens natur, vad som utgör ett bra liv, hur man skapar ett rättvist samhälle och så vidare., De ger sina svar på dessa frågor, och de stöder dessa svar med skäl. Då anser andra filosofer sina argument och svarar med utarbetningar och kritik—egna argument. Filosofin bedrivs och gör framsteg genom att utbyta argument. Eftersom de är det primära verktyget för sin handel, vet filosofer bättre lite något om vad som gör för goda argument! Logik är därför avgörande för filosofins praktik.,

men logik är inte bara ett verktyg för att utvärdera filosofiska argument; det har förändrat loppet av den pågående filosofiska konversationen. När logiker utvecklade formella system för att modellera strukturen hos ett allt bredare spektrum av diskursiva metoder har filosofer kunnat tillämpa sina insikter direkt på traditionella filosofiska problem och känna igen tidigare dolda undersökningsvägar. Sedan 1900-talet har spridningen av nya tillvägagångssätt i logik lett till en revolution i filosofins praktik., Det är inte för mycket av en överdrift att säga att mycket av filosofins historia under 1900-talet utgjorde ett pågående försök att brottas med ny utveckling i logik och det filosofiska fokus på språk som de tycktes kräva. Inget filosofiskt ämne—från metafysik till etik till epistemologi och bortom-var orörd av denna revolution.

slutligen är logiken själv källan till fascinerande filosofiska frågor. Den grundläggande frågan i sitt hjärta—Vad är det för ett påstående att följa från andra?,- ramifies ut i otaliga riktningar, vilket ger grogrund för filosofisk spekulation. Det finns logik, och då finns det logikens filosofi. Logik sägs vara ”formell”, till exempel. Vad betyder det? Det är en förvånansvärt svår fråga att svara på. Våra enklaste logiska formuleringar av villkorliga meningar (de som involverar ”if”) leder till uppenbara paradoxer. Hur ska de lösas? Bör våra formalismer ändras för att bättre fånga de naturliga språkbetydelserna av villkor? Vad är det rätta förhållandet mellan logiska system och naturliga språk?,

traditionellt har de flesta logiker accepterat att logiken ska vara ”bivalent”: varje proposition är antingen sann eller falsk. Men naturliga språk innehåller vaga termer vars tillämpningsgränser inte alltid är tydliga. Till exempel ”skallig”: för vissa ämnen kan vi vara benägna att säga att de är bra på väg till fullskallighet, men inte riktigt där än; å andra sidan skulle vi vara ovilliga att säga att de inte är skalliga. Det finns mellan fall. I sådana fall kanske vi till exempel vill säga att förslaget att Fredo är skallig varken är sant eller falskt., Vissa logiker har utvecklat logiker som inte är bivalenta, för att hantera denna typ av språkligt fenomen. Vissa lägger till ett tredje sanningsvärde: ”varken ” eller” obestämt”, till exempel. Andra introducerar oändliga sanningsgrader (detta kallas ”fuzzy logic”). Dessa logiker avviker från traditionella tillvägagångssätt. Är de därför fel på något sätt? Eller har de rätt, och traditionalisterna fel? Eller ställer vi till och med en förnuftig fråga när vi frågar om ett visst logiskt system är rätt eller fel?, Kan vi vara så kallade logiska ”pluralister”, acceptera en mängd inkompatibla logiker, beroende till exempel på om de är användbara?

dessa typer av frågor ligger naturligtvis utanför ramen för denna inledande text. De ingår för att ge dig en känsla av hur långt man kan ta studiet av logik. Uppgiften för nu är dock att börja den studien.