
Leonardo av Pisa (Fibonacci) (C.1170-1250)
den 13: e århundradet italienska Leonardo av Pisa, mer känd genom sitt smeknamn Fibonacci, var kanske den mest begåvade västerländska matematikern i Pisa.medeltiden. Lite är känt om sitt liv förutom att han var son till en tulloffical och som barn reste han runt Nordafrika med sin far, där han lärde sig om arabisk matematik., När han återvände till Italien hjälpte han till att sprida denna kunskap i hela Europa och satte därmed igång en föryngring i europeisk matematik, som i stor utsträckning hade legat vilande i århundraden under medeltiden.
i synnerhet i 1202 skrev han en enormt inflytelserik bok som heter ”Liber Abaci” (”Beräkningsbok”), där han främjade användningen av det hinduiska-arabiska numeriska systemet, som beskriver dess många fördelar för köpmän och matematiker både över det klumpiga systemet med romerska siffror som sedan användes i Europa., Trots sina uppenbara fördelar var upptagningen av systemet i Europa långsam (Det var trots allt under korstågen mot Islam, en tid då allt arabiska sågs med stor misstanke) och arabiska siffror förbjöds till och med i Florens 1299 under förevändning att de var lättare att förfalska än romerska siffror. Men sunt förnuft segrade så småningom och det nya systemet antogs i hela Europa på 1400-talet, vilket gör det romerska systemet föråldrat., Den horisontella stapelnotationen för fraktioner användes också först i detta arbete (även om man följde den arabiska praktiken att placera fraktionen till vänster om heltalet).
Fibonacci-sekvens

upptäckten av den berömda Fibonacci-sekvensen
Fibonacci är mest känd, men för att han introducerar en viss nummersekvens i Europa, som sedan dess har blivit känd som Fibonacci-nummer eller Fibonacci-sekvensen., Han upptäckte sekvensen-den första rekursiva nummersekvensen som är känd i Europa-samtidigt som han övervägde ett praktiskt problem i ”Liber Abaci” som involverar tillväxten av en hypotetisk population av kaniner baserat på idealiserade antaganden. Han noterade att efter varje månatlig generation ökade antalet par kaniner från 1 till 2 till 3 till 5 till 8 till 13, etc, och identifierade hur sekvensen utvecklades genom att lägga till de föregående två termerna (i matematiska termer, Fn = Fn-1 + Fn-2), en sekvens som i teorin skulle kunna sträcka sig på obestämd tid.,
sekvensen, som faktiskt hade varit känd för indiska matematiker sedan 6: e århundradet, har många intressanta matematiska egenskaper, och många av konsekvenserna och relationerna i sekvensen upptäcktes inte förrän flera århundraden efter Fibonaccis död., Till exempel regenererar sekvensen sig på några överraskande sätt: var tredje f-numret är delbart med 2 (F3 = 2), var fjärde f-numret är delbart med 3 (F4 = 3), var femte f-numret är delbart med 5 (F5 = 5), var sjätte f-numret är delbart med 8 (F6 = 8), var sjunde f-numret är delbart med 13 (F7 = 13) etc., Sekvensens nummer har också visat sig vara allestädes närvarande i naturen: bland annat har många arter av blommande växter antal kronblad i Fibonacci-sekvensen; spiralarrangemangen av ananas förekommer i 5s och 8s, pinecones i 8s och 13s, och frön av solroshuvuden i 21s, 34s, 55s eller ännu högre termer i sekvensen; etc.,
det gyllene förhållandet φ
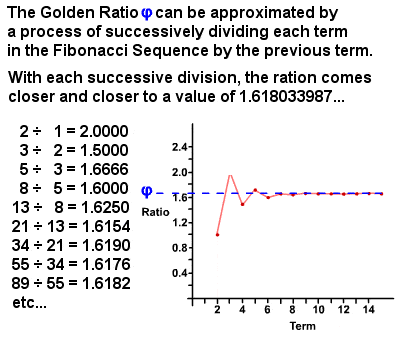
det gyllene förhållandet φ kan härledas från Fibonacci-sekvensen
på 1750-talet noterade Robert Simson att förhållandet mellan varje term i Fibonacci-sekvensen till föregående term närmar sig, med allt större noggrannhet desto högre villkor, ett förhållande på cirka 1 : 1.6180339887 (det är är faktiskt ett irrationellt tal som är lika med (1 + √5), som sedan dess har beräknats till tusentals decimaler)., Detta värde kallas det gyllene förhållandet, även känt som det gyllene medelvärdet, gyllene sektionen, gudomlig andel etc, och betecknas vanligtvis av det grekiska bokstaven phi φ (Eller ibland bokstaven Phi Φ). I huvudsak är två kvantiteter i det gyllene förhållandet om förhållandet mellan summan av kvantiteterna och den större kvantiteten är lika med förhållandet mellan den större kvantiteten och den mindre. Det gyllene förhållandet i sig har många unika egenskaper, till exempel 1. φ = φ – 1 (0,618…) och φ2 = φ + 1 (2,618…), och det finns otaliga exempel på det som finns både i naturen och i den mänskliga världen.,
en rektangel med sidor i förhållandet 1: φ är känd som en gyllene rektangel, och många konstnärer och arkitekter genom historien (som går tillbaka till det antika Egypten och Grekland, men särskilt populär i renässanskonsten Leonardo Da Vinci och hans samtidiga) har proportionerat sina verk ungefär med hjälp av det gyllene förhållandet och gyllene rektanglar, som allmänt anses vara medfödd estetiskt tilltalande. En båge som förbinder motsatta punkter av allt mindre kapslade gyllene rektanglar bildar en logaritmisk spiral, känd som en gyllene Spiral., Det gyllene förhållandet och den gyllene spiralen kan också hittas i ett överraskande antal instanser i naturen, från skal till blommor till djurhorn till mänskliga kroppar till stormsystem för att slutföra galaxer.,
man bör dock komma ihåg att Fibonacci – sekvensen faktiskt bara var ett mycket mindre element i ”Liber Abaci” – i själva verket fick sekvensen endast Fibonaccis namn 1877 när Eduouard Lucas bestämde sig för att hylla honom genom att namnge serien efter honom-och att Fibonacci själv inte var ansvarig för att identifiera någon av de intressanta matematiska egenskaperna i sekvensen, dess förhållande till de gyllene medelvärdet och gyllene rektanglarna och spiralerna etc.,
Gittermultiplikation
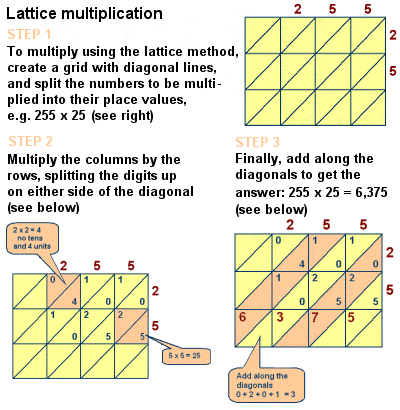
Fibonacci introducerade gittermultiplikation till Europa
bokens inflytande på medeltida matematik är dock obestridligt, och det innehåller också diskussioner om ett antal andra matematiska problem som den kinesiska återstoden teorem, perfekta tal och primtal, formler för aritmetiska serier och för kvadratiska pyramidala tal, euklidiska geometriska bevis, och en studie av samtidiga linjära ekvationer i linje med Diophantus och Al-karaji., Han beskrev också lattice (eller sieve) multiplikationsmetoden för att multiplicera stora tal, en metod – ursprungligen pionjär av islamiska matematiker som Al-Khwarizmi – algoritmiskt ekvivalent med lång multiplikation.
inte heller var ”Liber Abaci” Fibonacci enda bok, även om det var hans viktigaste., Hans ”Liber Quadratorum” (”The Book of Squares”), till exempel, är en bok om algebra, som publicerades i 1225 där visas en förklaring av vad som nu kallas Fibonacci identitet – ibland även kallad Brahmagupta identitet efter mycket tidigare Indiska matematiker som också kommit till samma slutsats – att produkten av två summor av två rutor är själv en summa av två rutor, t ex (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |