läranderesultat
- bekanta sig med historien om positionella nummersystem
- identifiera baser som har använts i nummersystem historiskt
- konvertera siffror mellan baser
- använd två olika metoder för att konvertera siffror mellan baser
Bakgrund
som en man kan tänka sig att utvecklingen av ett bassystem är ett viktigt steg för att göra räkningsprocessen effektivare., Vårt eget bas-tio-system uppstod förmodligen av det faktum att vi har 10 fingrar (inklusive tummar) på två händer. Detta är en naturlig utveckling. Men andra civilisationer har haft en mängd andra baser än tio. Till exempel använde infödingarna i Queensland ett bas-två-system och räknade enligt följande: ”en, två, två och en, två två, mycket.”Vissa moderna sydamerikanska stammar har ett bas-fem system som räknar på detta sätt: ”en, två, tre, fyra, hand, hand och en, hand och två” och så vidare. Babylonierna använde ett bas-sextio (sexigesimal) system., I detta kapitel avslutar vi med ett specifikt exempel på en civilisation som faktiskt använde ett annat bassystem än 10.
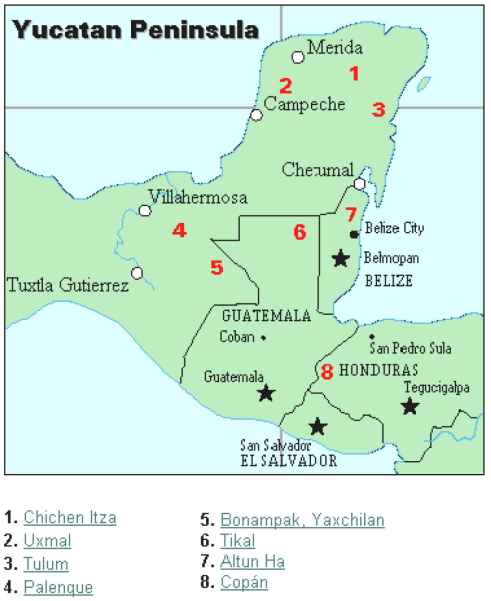 Maya civilisationen är i allmänhet daterad från 1500 BCE till 1700 CE. Yucatanhalvön (se figur 16) i Mexiko var scenen för utvecklingen av en av de mest avancerade civilisationerna i den antika världen. Mayanerna hade ett sofistikerat ritualsystem som övervakades av en prästerlig klass. Denna klass av präster utvecklade en filosofi med tiden som gudomlig och evig., Kalendern och beräkningarna relaterade till den var således mycket viktiga för den prästliga klassens rituella liv, och därmed Maya-folket. Faktum är att mycket av vad vi vet om denna kultur kommer från deras kalenderposter och astronomidata. En annan viktig informationskälla om Mayanerna är fader Diego de landas skrifter, som åkte till Mexiko som missionär 1549.
Maya civilisationen är i allmänhet daterad från 1500 BCE till 1700 CE. Yucatanhalvön (se figur 16) i Mexiko var scenen för utvecklingen av en av de mest avancerade civilisationerna i den antika världen. Mayanerna hade ett sofistikerat ritualsystem som övervakades av en prästerlig klass. Denna klass av präster utvecklade en filosofi med tiden som gudomlig och evig., Kalendern och beräkningarna relaterade till den var således mycket viktiga för den prästliga klassens rituella liv, och därmed Maya-folket. Faktum är att mycket av vad vi vet om denna kultur kommer från deras kalenderposter och astronomidata. En annan viktig informationskälla om Mayanerna är fader Diego de landas skrifter, som åkte till Mexiko som missionär 1549.
 det fanns två siffersystem som utvecklats av Mayans—en för det vanliga folket och en för prästerna., Inte bara använde dessa två system olika symboler, de använde också olika bassystem. För prästerna styrdes nummersystemet av ritual. Årets dagar troddes vara gudar, så de formella symbolerna för dagarna var dekorerade huvuden, som provet till vänster sedan grundkalendern baserades på 360 dagar, det prästliga numeriska systemet använde ett blandat bassystem som använde multiplar av 20 och 360. Detta gör ett förvirrande system, detaljerna som vi kommer att hoppa över.,/td>
det fanns två siffersystem som utvecklats av Mayans—en för det vanliga folket och en för prästerna., Inte bara använde dessa två system olika symboler, de använde också olika bassystem. För prästerna styrdes nummersystemet av ritual. Årets dagar troddes vara gudar, så de formella symbolerna för dagarna var dekorerade huvuden, som provet till vänster sedan grundkalendern baserades på 360 dagar, det prästliga numeriska systemet använde ett blandat bassystem som använde multiplar av 20 och 360. Detta gör ett förvirrande system, detaljerna som vi kommer att hoppa över.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the ”common” people, which used a more consistent base system., Som vi sa tidigare använde Mayans ett bas-20-system, kallat ”vigesimal” – systemet. Liksom vårt system är det positionellt, vilket innebär att positionen för en numerisk symbol indikerar sitt platsvärde. I följande tabell kan du se platsvärdet i sitt vertikala format.
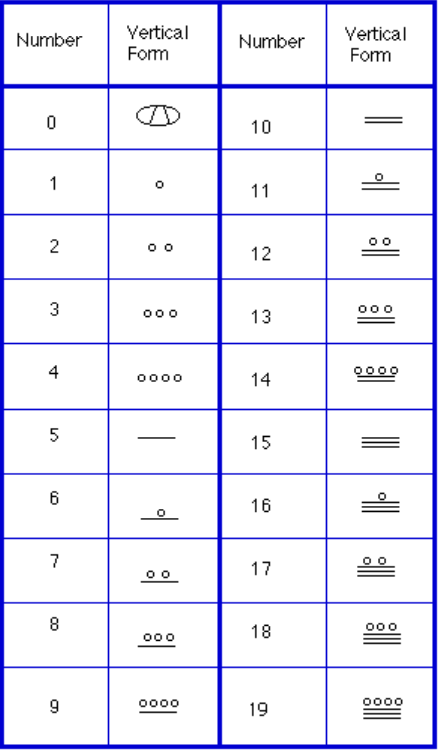
för att skriva ner siffror behövdes det bara tre symboler i det här systemet. En horisontell stapel representerade kvantiteten 5, en prick representerade kvantiteten 1, och en speciell symbol (tros vara ett skal) representerade noll., Maya-systemet kan ha varit det första som använder sig av noll som platshållare/nummer. De första 20 siffrorna visas i tabellen till höger.
Till skillnad från vårt system, där de plats börjar till höger och sedan flyttar till vänster, Maya-system placerar de på botten av en vertikal orientering och rör sig uppåt när platsvärdet ökar.
När siffror skrivs i vertikal form, bör det aldrig finnas mer än fyra punkter på ett enda ställe. När du skriver Maya-nummer blir varje grupp av fem punkter en bar., Dessutom bör det aldrig finnas mer än tre barer på ett enda ställe … fyra barer skulle omvandlas till en punkt på nästa plats upp. Det är samma som 10 att omvandlas till en 1 på nästa plats när vi bär under Tillägg.
exempel
vad är värdet för detta nummer, vilket visas i vertikal form?
exempel
vad är värdet för följande Maya-nummer?,
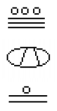
prova det
konvertera Maya-numret nedan till bas 10.,

exempel
konvertera basen 10 nummer 357510 till Maya siffror.
skriva siffror med baser större än 10
när basen av ett tal är större än 10, separera varje ”siffra” med ett kommatecken för att göra separationen av siffror tydlig.
till exempel, i bas 20, för att skriva numret som motsvarar 17 × 202 + 6 × 201 + 13 × 200, vi skulle skriva 17,6,1320.
i följande video presenterar vi fler exempel på hur man skriver siffror med Maya siffror samt konvertera siffror skrivna i Maya för till bas 10 form.,
nästa video visar fler exempel på att konvertera bas 10-tal till Maya-siffror.
lägga till Maya-nummer
När du lägger till Maya-nummer tillsammans antar vi ett system som Mayans förmodligen inte använde men som gör livet lite lättare för oss.
exempel
Lägg till, i Maya, siffrorna 37 och 29:

prova det
försök att lägga till 174 och 78 i Maya genom att först konvertera till Maya-nummer och sedan arbeta helt inom det systemet. Lägg inte till i bas-tio (decimal) till slutet när du kontrollerar ditt arbete.
i den senaste videon visar vi fler exempel på att lägga till Maya-siffror.,
i den här modulen har vi kortfattat skisserat utvecklingen av siffror och vårt räkningssystem, med betoning på ”kort” delen. Det finns många källor till information och forskning som fyller många volymer böcker om detta ämne. Tyvärr kan vi inte börja komma nära att täcka all information som finns där ute.

Vi har bara repat ytan av den rikedom av forskning och information som finns på utvecklingen av siffror och räknar genom hela mänsklighetens historia., Det som är viktigt att notera är att det system som vi använder varje dag är en produkt av tusentals år av framsteg och utveckling. Det representerar bidrag från många civilisationer och kulturer. Det kommer inte ner till oss från himlen, en gåva från gudarna. Det är inte skapandet av en lärobok utgivare. Det är verkligen lika mänskligt som vi är, liksom resten av matematiken. Bakom varje symbol, formel och regel finns ett mänskligt ansikte att hitta, eller åtminstone söka.
dessutom hoppas vi att du nu har en grundläggande uppskattning för hur intressanta och olika antal system kan få., Vi är också ganska säkra på att du också har börjat inse att vi tar vårt eget nummersystem för givet så mycket att när vi försöker anpassa oss till andra system eller baser, befinner vi oss verkligen behöva koncentrera oss och tänka på vad som händer.







