Verwandte Ressourcen: Materialwissenschaft
Abschnitt Modulgleichungen und-rechner Gemeinsame Formen
Materialstärke | Strahlauslenkung und Spannung
Abschnitt Modul ist eine geometrische Eigenschaft für einen bestimmten Querschnitt, die bei der Gestaltung von Balken oder Biegeelementen verwendet wird. Andere geometrische Eigenschaften, die im Design verwendet werden, umfassen Bereich für Spannung, Radius der Gyration für Kompression und Trägheitsmoment für Steifigkeit., Jede Beziehung zwischen diesen Eigenschaften hängt stark von der fraglichen Form ab. Gleichungen für die Schnittmodule gängiger Formen sind unten angegeben. Es gibt zwei Arten von Schnittmodulen, den Elastizitätsmodul (S) und den Kunststoffschnittsmodul (Z).
Für das allgemeine Design wird der Elastizitätsmodul verwendet, der für die meisten Metalle und andere gebräuchliche Materialien bis zur Streckgrenze gilt.
Der Elastizitätsmodul ist definiert als S = I / y, wobei I das zweite Moment der Fläche (oder Trägheitsmoment) und y der Abstand von der Neutralachse zu einer gegebenen Faser ist., Es wird häufig berichtet, dass y = c verwendet wird , wobei c der Abstand von der Neutralachse zur extremsten Faser ist, wie in der folgenden Tabelle zu sehen ist. Es wird auch häufig verwendet, um das Streckmoment (My) so zu bestimmen, dass My = S × σy, wobei σy die Streckgrenze des Materials ist.,p>
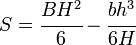
Calculator:
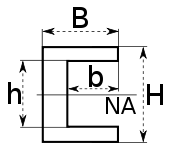
Section Modulus Channel Shape Center Neutral Axis Calculator
Plastic Section Modulus (PNA)
The Plastic section modulus is used for materials where (irreversible) plastic behavior is dominant., Die meisten Designs stoßen nicht absichtlich auf dieses Verhalten.
Der Kunststoffquerschnittsmodul hängt von der Lage der Kunststoffneutralachse (PNA) ab. Die PNA ist definiert als die Achse, die den Querschnitt so spaltet, dass die Druckkraft aus dem Bereich der Kompression der Zugkraft aus dem Bereich der Spannung entspricht. Für Abschnitte mit konstanter nachgiebiger Spannung ist also die Fläche über und unter der PNA gleich, aber für zusammengesetzte Abschnitte ist dies nicht unbedingt der Fall.,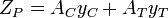
- Abschnitt Modul Gleichungen und Rechner
- Abschnitt Eigenschaften Radius von Gyration Fällen 1-10
- Abschnitt Eigenschaften Radius von Gyration Fällen 11-16
- Abschnitt Eigenschaften Radius von Gyration Fällen 17-22
- Abschnitt Eigenschaften Radius von Gyration Fällen 23-27
- Abschnitt Eigenschaften Radius von Gyration Fällen 28-31
- Abschnitt Eigenschaften Radius von Gyration Fällen 32-34
- Abschnitt Eigenschaften Radius von Gyration Fällen 35-37

![]()