tato část se zabývá binomickou větou a Pascalovým trojúhelníkem.
pascalova Trojúhelníku,
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
měli byste Si všimnout, že koeficienty (čísla před) a a b jsou:
1 1
1 2 1
1 3 3 1
Pokud máte i nadále rozšiřuje držáky pro vyšší síly, měli byste zjistit, že sekvence pokračuje:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
atd
Tato sekvence je známý jako pascalův trojúhelník., Každé z čísel je nalezeno přidáním dvou čísel přímo nad ním.
takže 20 v posledním řádku je nalezeno přidáním 10 a 10. Každý z 10s v řádku výše jsou nalezeny přidáním dohromady 6 a 4.
takže je možné rozšířit (a + b) na libovolný počet výkon tím, že zná Pascal trojúhelník.
příklad
najít (3 + x) 3
síla, na kterou rozšiřujeme konzolu, je 3, takže se podíváme na třetí řádek Pascalova trojúhelníku, což je 1 3 3 1.,
Takže odpověď je: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(můžeme nahradit tím, že 3 a b o x v rozšíření (a + b)3 výše),
Obecně
To je, samozřejmě, často nepraktické psát Pascal“s trojúhelník, pokaždé, když vše, co potřebujeme vědět, jsou údaje o n-tému řádku. Je zřejmé, že první číslo na n. řádku je 1. Druhé číslo je n. třetí číslo je:
n (n – 1).
1 × 2
obecně platí, že číslo rth v řádku nth je:
n! (což je nCr na kalkulačce)
r! (n – r)!
kde n!, znamená „n faktoriál“ a rovná se n × (n-1) × … × 2 × 1
nCr je také často psáno jako 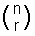 a vyslovuje se „n zvolte r“.
a vyslovuje se „n zvolte r“.
Binomickou Větu,
Binomická Věta uvádí, že:, kde n je kladné celé číslo.
-
(a + b)n = an + (nC1)-1b + (nC2)-2b2 + … + (nCn-1)abn-1 + bn
Příklad:
Rozšířit (4 + 2x)6 ve vzestupném pravomoci x až termín v x3
Tento prostředek používat Binomickou větu rozšířit pojmy v závorkách, ale jít jen tak vysoko, jako x3.,
Takže chcete najít odpověď dosadíme 4 v Binomická věta a 2x pro b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Binomické Věty (1 + x)n
předchozí verze binomická věta funguje pouze tehdy, když n je kladné celé číslo., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
POSKYTOVÁNÍ |x| < 1.
Všimněte si, že zatímco předchozí série se zastaví, tenhle jde na věčnost.
Příklad:
Najít rozšíření (5x + 2)1/2
Musíme proměnit to, tak to vypadá, že (1 + x)1/2, takže umožňuje vzít ven faktor 2:
(5x + 2)1/2 = (2)1/2
Nyní, kde máme ‚x‘ na výše uvedeném vzorci, potřebujeme 5x/2 a kde máme n, potřebujeme½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Pamatujte, že toto platí, pouze pokud -1 < 5x/2 < 1, jinými slovy, -2/5 < x < 2/5
Pomocí Parciální Zlomky
můžeme rozšířit složitější výrazy, nyní, pomocí metody parciálních zlomků, kde je to vhodné.
příklad