Dieser Abschnitt befasst sich mit Binomial-Theorem und Pascals Dreieck.
Pascal ‚ s Triangle
also (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
sollten Sie beachten, dass die Koeffizienten (die zahlen vor), a und b sind:
1 1
1 2 1
1 3 3 1
Wenn Sie baute die Klammern für höhere Mächte, würden Sie finden, dass die Sequenz weiter:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
Diese Sequenz ist bekannt als Pascal ‚ s triangle., Jede der Zahlen wird gefunden, indem die beiden Zahlen direkt darüber addiert werden.
So wird die 20 in der letzten Zeile durch Addieren von 10 und 10 gefunden. Jede der 10s in der obigen Zeile wird gefunden, indem eine 6 und eine 4 addiert werden.
So ist es möglich, (a + b) auf eine beliebige ganze Zahl zu erweitern, indem man Pascals Dreieck kennt.
Beispiel
Find (3 + x)3
Die Potenz, auf die wir die Klammer erweitern, ist 3, also schauen wir uns die dritte Zeile von Pascals Dreieck an, die 1 3 3 1 ist.,
Die Antwort lautet also: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3 (wir ersetzen a durch 3 und b durch x in der Erweiterung von (a + b)3 oben)
Im Allgemeinen
Es ist natürlich oft unpraktisch, jedes Mal Pascals Dreieck auszuschreiben, wenn wir nur die Einträge in der n-ten Zeile kennen müssen. Die erste Zahl in der n-ten Zeile ist eindeutig 1. Die zweite Zahl ist n. Die dritte Zahl ist:
n (n – 1) .
1 × 2
Im Allgemeinen lautet die rth-Zahl in der n-ten Zeile:
n! (das ist nCr auf Ihrem Rechner)
r! (n – r)!
wo n!, bedeutet ’n factorial‘ und ist gleich n × (n-1) × … × 2 × 1
nCr wird auch oft als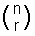 
geschrieben und wird ausgesprochen „n wählen r“.
Der Binomialsatz
Der Binomialsatz besagt, dass, wobei n eine positive Ganzzahl ist:
-
(a + b)n = an + (nC1)an-1b + (nC2)an-2b2 + … + (nCn-1)abn-1 + bn
Beispiel
Expand (4 + 2x)6 in aufsteigenden Potenzen von x bis für den Begriff in x3
bedeutet dies, den Binomialsatz zu verwenden, um die Begriffe in den Klammern zu erweitern, aber nur so hoch wie x3 zu gehen.,
Um die Antwort zu finden, ersetzen wir 4 für a im Binomialsatz und 2x für b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Der Binomialsatz für (1 + x)n
Die vorherige Version des Binomialsatzes funktioniert nur, wenn n eine positive Ganzzahl ist., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
x|< 1
Beachten Sie, dass, während die vorherige Serie stoppt, diese für immer weitergeht.
Beispiel
Finden Sie die Erweiterung von (5x + 2)1/2
Wir müssen dies transformieren, damit es wie (1 + x)1/2 aussieht, also nehmen wir einen Faktor von 2 heraus:
(5x + 2)1/2 = (2)1/2
Jetzt, wo wir ‚x‘ in der obigen Formel haben, brauchen wir 5x/2 und wo wir n haben, brauchen wir½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Denken Sie daran, dies ist nur gültig, wenn -1 < 5x/2 < 1, mit anderen Worten, -2/5 < x < 2/5
Mit partiellen Brüchen
können wir kompliziertere Ausdrücke erweitern, jetzt mit der Methode der partiellen Brüche gegebenenfalls.
Beispiel