de 5 Clustering algoritmer data forskere har brug for at vide

Jeg har for nylig startet en bog-fokuseret pædagogisk nyhedsbrev. Book Dives er et ugentligt nyhedsbrev, hvor vi for hver ny udgave dykker ned i en non-fiction bog. Du lærer om bogens kernelektioner og hvordan man anvender dem i det virkelige liv. Du kan abonnere på det her.

Clustering er en maskinindlæringsteknik, der involverer gruppering af datapunkter. I betragtning af et sæt datapunkter kan vi bruge en klyngealgoritme til at klassificere hvert datapunkt i en bestemt gruppe., I teorien skal datapunkter, der er i samme gruppe, have lignende egenskaber og/eller funktioner, mens datapunkter i forskellige grupper skal have meget forskellige egenskaber og / eller funktioner. Clustering er en metode til uovervåget læring og er en almindelig teknik til statistisk dataanalyse, der anvendes på mange områder.

i datavidenskab kan vi bruge klyngeanalyse til at få nogle værdifulde indsigter fra vores data ved at se, hvilke grupper datapunkterne falder ind i, når vi anvender en klyngealgoritme., I dag skal vi se på 5 populære klyngealgoritmer, som dataforskere har brug for at kende og deres fordele og ulemper!

k-betyder klyngedannelse

K-midler er sandsynligvis den mest kendte klyngealgoritme. Det er undervist i en masse indledende data videnskab og machine learning klasser. Det er let at forstå og implementere i kode! Tjek grafikken nedenfor for en illustration.,

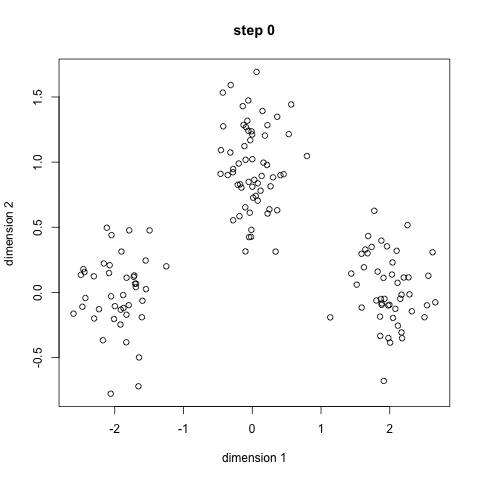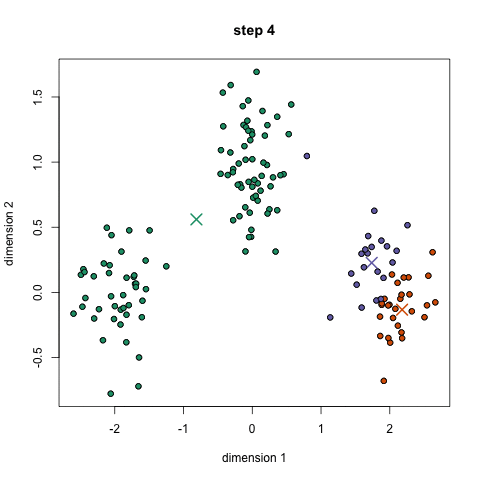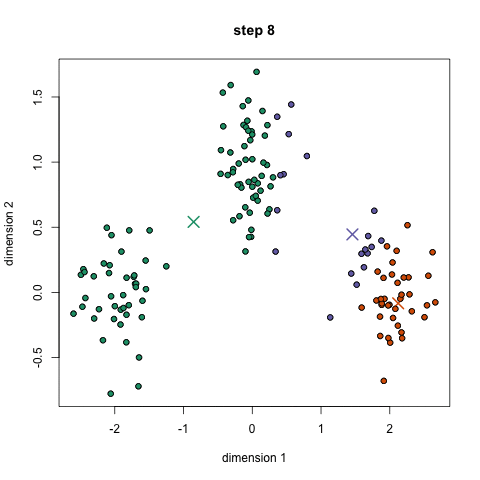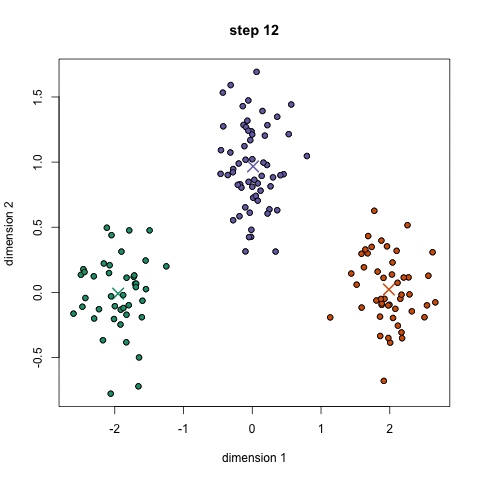
1. til At begynde, vi ved først at vælge et antal klasser/grupper til at bruge og tilfældigt initialisere deres respektive center point. For at finde ud af antallet af klasser, der skal bruges, er det godt at tage et hurtigt kig på dataene og forsøge at identificere eventuelle forskellige grupperinger. Midtpunkterne er vektorer af samme længde som hver datapunktvektor og er “X ‘ erne” i grafikken ovenfor.,
2. hvert datapunkt klassificeres ved at beregne afstanden mellem dette punkt og hvert gruppecenter og derefter klassificere det punkt, der skal være i gruppen, hvis centrum er tættest på det.
3. baseret på disse klassificerede punkter beregner vi gruppecentret igen ved at tage gennemsnittet af alle vektorer i gruppen.
4. Gentag disse trin for et bestemt antal iterationer, eller indtil gruppecentrene ikke ændrer meget mellem iterationer. Du kan også vælge at initialisere gruppecentrene tilfældigt et par gange, og vælg derefter det løb, der ser ud som om det gav de bedste resultater.,

K-midler har den fordel, at det er ret hurtigt, da alt, hvad vi virkelig gør, er at beregne afstandene mellem punkter og gruppecentre; meget få beregninger! Det har således en lineær kompleksitet O (n).

På den anden side har K-midler et par ulemper. For det første skal du vælge, hvor mange grupper/klasser der er. Dette er ikke altid trivielt og ideelt med en klyngealgoritme, vi ønsker, at den skal finde ud af dem for os, fordi pointen med det er at få en vis indsigt fra dataene., K-midler starter også med et tilfældigt valg af klyngecentre, og det kan derfor give forskellige klyngeresultater på forskellige kørsler af algoritmen. Således kan resultaterne ikke være gentagelige og mangler konsistens. Andre klyngemetoder er mere konsistente.

K-Medians er en anden klyngealgoritme relateret til K-midler, undtagen i stedet for at omregne gruppecenterpunkterne ved hjælp af gennemsnittet bruger vi medianvektoren i gruppen., Denne metode er mindre følsom over for outliers (på grund af at bruge medianen), men er meget langsommere for større datasæt, da sortering er påkrævet på hver iteration, når man beregner Medianvektoren.

Mean-Shift Clustering

Mean shift clustering er en glidende vinduesbaseret algoritme, der forsøger at finde tætte områder af datapunkter. Det er en centroid-baseret algoritme, der betyder, at målet er at finde midtpunkterne for hver gruppe/klasse, som fungerer ved at opdatere kandidater til, at centerpunkter er middelværdien af punkterne i glidevinduet., Disse kandidatvinduer filtreres derefter i et efterbehandlingstrin for at eliminere næsten duplikater, der danner det sidste sæt midtpunkter og deres tilsvarende grupper. Tjek grafikken nedenfor for en illustration.

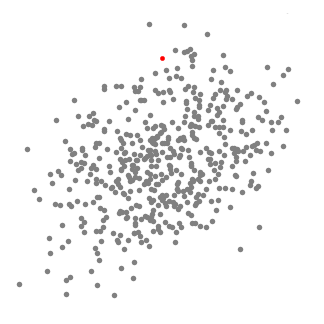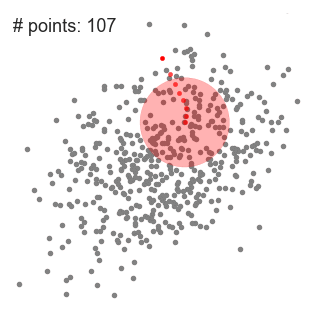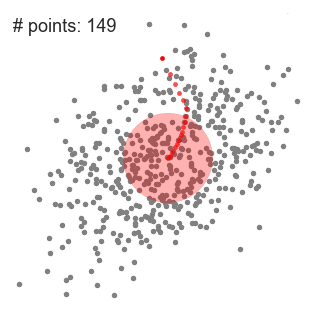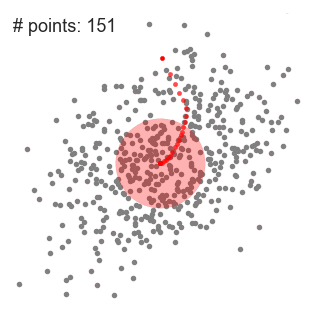
1. At forklare betyde-skift, vi vil overveje en række punkter i det to-dimensionelle rum som ovenstående illustration., Vi begynder med et cirkulært glidevindue centreret på et punkt C (tilfældigt valgt) og har radius r som kernen. Mean shift er en bjergbestigningsalgoritme, der involverer at skifte denne kerne iterativt til et område med højere densitet på hvert trin indtil konvergens.
2. ved hver iteration forskydes glidevinduet mod områder med højere densitet ved at flytte midtpunktet til gennemsnittet af punkterne i vinduet (deraf navnet). Tætheden inden for glidevinduet er proportional med antallet af punkter inde i det., Ved at skifte til middelværdien af punkterne i vinduet vil det naturligvis gradvist bevæge sig mod områder med højere punkttæthed.
3. Vi fortsætter med at flytte skydevinduet i henhold til middelværdien, indtil der ikke er nogen retning, hvor et skift kan rumme flere punkter inde i kernen. Tjek grafikken ovenfor; vi fortsætter med at flytte cirklen, indtil vi ikke længere øger densiteten (dvs.antal punkter i vinduet).
4. denne proces med trin 1 til 3 udføres med mange glidende vinduer, indtil alle punkter ligger inden for et vindue., Når flere skydevinduer overlapper vinduet, der indeholder flest punkter, bevares. Datapunkterne grupperes derefter i henhold til det glidende vindue, hvor de bor.

en illustration af hele processen fra ende til ende med alle de glidende vinduer er vist nedenfor. Hver sort prik repræsenterer centroid af en glidende vindue og hver grå prik er et datapunkt.,

I modsætning til K-means clustering, der er ingen grund til at vælge antallet af klynger, som betyder,-shift automatisk opdager dette. Det er en stor fordel. Det faktum, at klyngecentrene konvergerer mod punkterne med maksimal densitet, er også ret ønskeligt, da det er ret intuitivt at forstå og passer godt i en naturligt datadrevet forstand., Ulempen er, at valget af vinduets størrelse/radius “r” kan være ikke-trivielt.

Densitetsbaseret rumlig klynge af applikationer med støj (DBSCAN)

DBSCAN er en densitetsbaseret grupperet algoritme, der ligner mean-shift, men med et par bemærkelsesværdige fordele. Tjek en anden fancy grafik nedenfor og lad os komme i gang!,

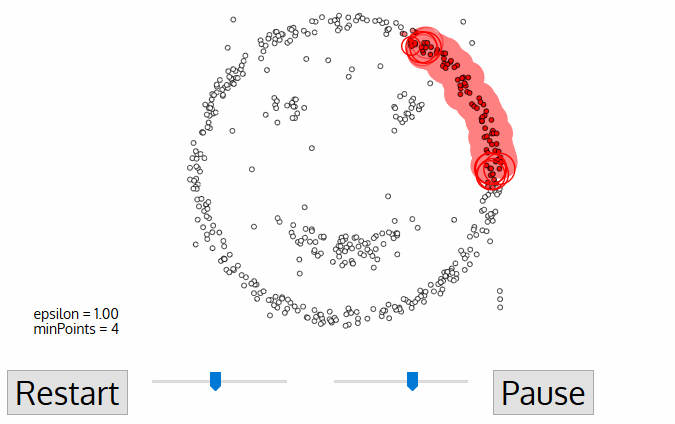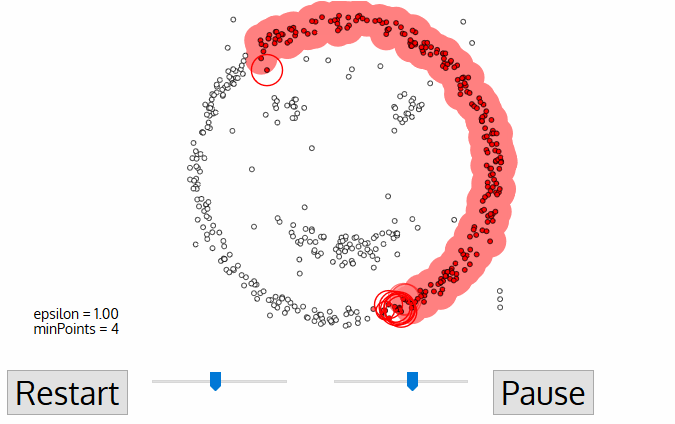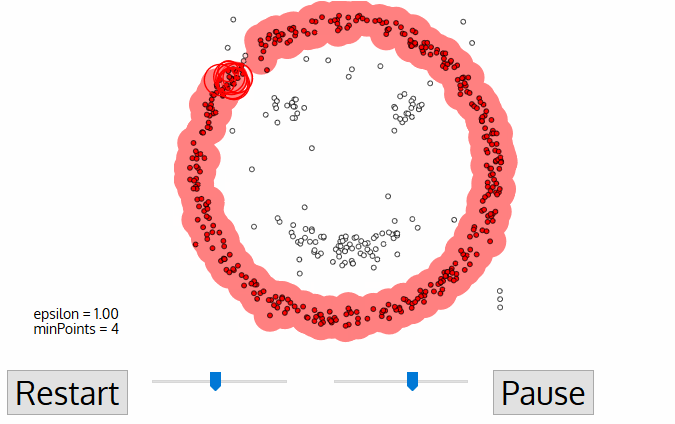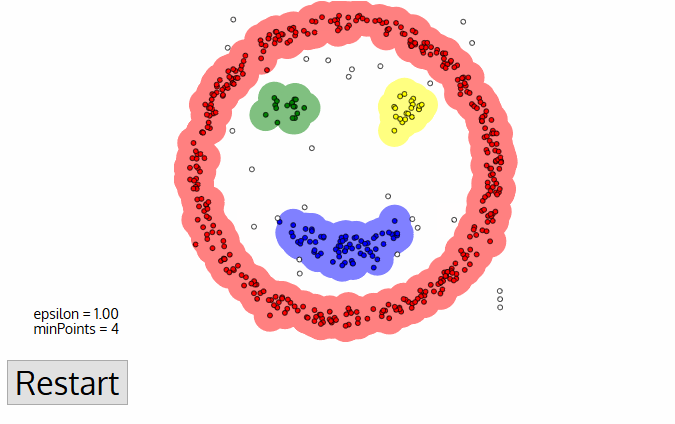
1. DBSCAN begynder med en vilkårlig starter data punkt, der har ikke har været besøgt. Kvarteret af dette punkt udvindes ved hjælp af en afstand epsilon ε (alle punkter, som er inden for distance afstand er kvarter punkter).,
2. hvis der er et tilstrækkeligt antal point (ifølge minPoints) inden for dette kvarter, starter klyngeprocessen, og det aktuelle datapunkt bliver det første punkt i den nye klynge. Ellers vil punktet blive mærket som støj (senere kan dette støjende punkt blive den del af klyngen). I begge tilfælde er dette punkt markeret som “besøgt”.
3. for dette første punkt i den nye klynge bliver punkterne inden for sit ε-distancekvarter også en del af den samme klynge., Denne procedure med at gøre alle punkter i neighborhood-kvarteret tilhører den samme klynge gentages derefter for alle de nye punkter, der netop er tilføjet til klyngegruppen.
4. denne proces med trin 2 og 3 gentages, indtil alle punkter i klyngen er bestemt, dvs.alle punkter i cluster-kvarteret i klyngen er blevet besøgt og mærket.
5. når vi er færdige med den aktuelle klynge, hentes og behandles et nyt ubesøgt punkt, hvilket fører til opdagelsen af en yderligere klynge eller støj. Denne proces gentages, indtil alle punkter er markeret som besøgt., Da alle punkter i slutningen af dette er besøgt, vil hvert punkt være markeret som enten tilhørende en klynge eller være støj.

DBSCAN udgør nogle store fordele i forhold til andre klyngealgoritmer. For det første kræver det slet ikke et pe-sæt antal klynger. Det identificerer også outliers som lyde, i modsætning til mean-shift, som blot kaster dem ind i en klynge, selvom datapunktet er meget anderledes. Derudover kan den finde vilkårligt store og vilkårligt formede klynger ganske godt.,

den største ulempe ved DBSCAN er, at den ikke fungerer så godt som andre, når klyngerne har forskellig densitet. Dette skyldes, at indstillingen af afstandstærsklen ε og minPoints til identifikation af kvarterets punkter vil variere fra klynge til klynge, når densiteten varierer. Denne ulempe forekommer også med meget højdimensionelle data, da afstandstærsklen again igen bliver udfordrende at estimere.,

Expectation–Maximization (EM) Klyngedannelse ved hjælp af Gauss-Blanding Modeller (GMM)

En af de store ulemper af K-Midler er dens naive brug af den gennemsnitlige værdi for klyngens centrum. Vi kan se, hvorfor dette ikke er den bedste måde at gøre ting ved at se på billedet nedenfor. På venstre side ser det helt åbenlyst ud for det menneskelige øje, at der er to cirkulære klynger med forskellig radius’ centreret på samme middelværdi. K-midler kan ikke håndtere dette, fordi middelværdierne af klyngerne er meget tæt sammen., K-betyder også mislykkes i tilfælde, hvor klyngerne ikke er cirkulære, igen som et resultat af at bruge middelværdien som klyngecenter.

Gauss Blanding Modeller (Gmm) giver os mere fleksibilitet end K-Midler. Med GMM ‘ er antager vi, at datapunkterne er gaussiske fordelt; dette er en mindre restriktiv antagelse end at sige, at de er cirkulære ved at bruge middelværdien., På den måde har vi to parametre til at beskrive formen på klyngerne: middelværdien og standardafvigelsen! Ved at tage et eksempel i to dimensioner betyder det, at klyngerne kan tage enhver form for elliptisk form (da vi har en standardafvigelse i både directions-og y-retningerne). Således er hver Gaussisk distribution tildelt en enkelt klynge.

for at finde parametrene for den gaussiske for hver klynge (f.eks.middel–og standardafvigelsen), bruger vi en optimeringsalgoritme kaldet E .pectation-Ma .imi .ation (EM)., Tag et kig på grafikken nedenfor som en illustration af Gausserne, der er monteret på klyngerne. Så kan vi fortsætte med processen med forventning–maksimering clustering hjælp GMMs.

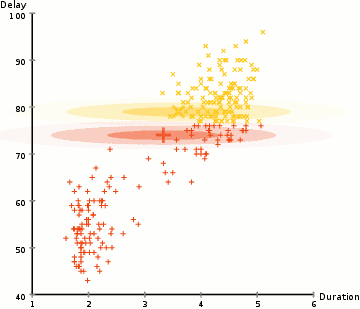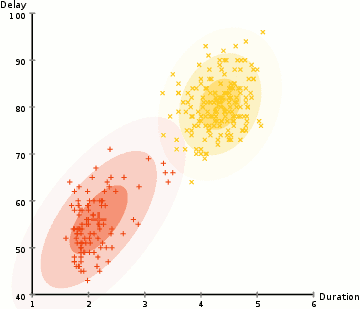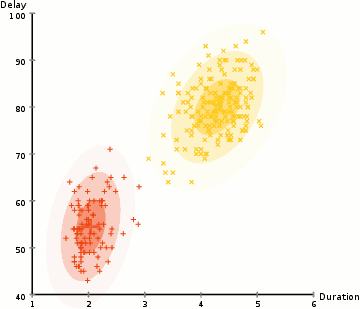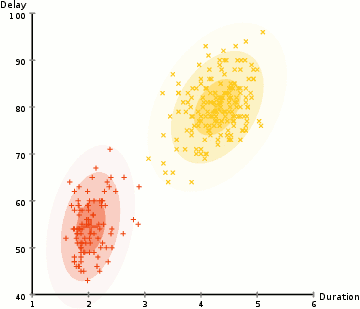
1. Vi begynder med at vælge det antal klynger (som K-Betyder) og tilfældigt initialisering af den Gaussiske fordeling parametre for hver klynge., Man kan forsøge at give en god guesstimate for de indledende parametre ved at tage et hurtigt kig på data også. Selvom Bemærk, Som det kan ses i grafikken ovenfor, er dette ikke 100% nødvendigt, da Gausserne starter vores som meget fattige, men optimeres hurtigt.
2. i betragtning af disse gaussiske distributioner for hver klynge skal du beregne sandsynligheden for, at hvert datapunkt hører til en bestemt klynge. Jo tættere et punkt er på Gaussens centrum, jo mere sandsynligt hører det til denne klynge., Dette skulle give intuitiv mening, da vi med en Gaussisk distribution antager, at de fleste af dataene ligger tættere på centrum af klyngen.
3. baseret på disse sandsynligheder beregner vi et nyt sæt parametre for de gaussiske distributioner, så vi maksimerer sandsynlighederne for datapunkter i klyngerne. Vi beregner disse nye parametre ved hjælp af en vægtet sum af datapunktspositionerne, hvor vægtene er sandsynlighederne for datapunktet, der hører til den pågældende klynge., For at forklare dette visuelt kan vi se på grafikken ovenfor, især den gule klynge som et eksempel. Fordelingen starter tilfældigt på den første iteration, men vi kan se, at de fleste af de gule punkter er til højre for denne fordeling. Når vi beregner en sum vægtet af sandsynlighederne, selvom der er nogle punkter nær centrum, er de fleste af dem til højre. Således naturligvis fordelingen middelværdi forskydes tættere på disse sæt af punkter. Vi kan også se, at de fleste af punkterne er “top-højre til bund-venstre”., Derfor ændres standardafvigelsen for at skabe en ellipse, der er mere monteret på disse punkter, for at maksimere summen vægtet af sandsynlighederne.
4. Trin 2 og 3 gentages iterativt indtil konvergens, hvor distributionerne ikke ændrer meget fra iteration til iteration.

der er 2 vigtige fordele ved at bruge GMM ‘ er. For det første er GMM ‘ er meget mere fleksible med hensyn til klyngekovarians end k-midler; på grund af standardafvigelsesparameteren kan klyngerne påtage sig enhver ellipsform snarere end at være begrænset til cirkler., K-midler er faktisk et specielt tilfælde af GMM, hvor hver klynges kovarians langs alle dimensioner nærmer sig 0. For det andet, da GMM ‘ er bruger sandsynligheder, kan de have flere klynger pr. Så hvis et datapunkt er midt i to overlappende klynger, kan vi blot definere sin klasse ved at sige, at den tilhører class-procent til klasse 1 og Y-procent til klasse 2. Dvs GMMs støtte blandet medlemskab.

Agglomerative hierarkiske Clustering

hierarkiske clustering algoritmer falder i 2 Kategorier: top-do .n eller bottom-up., Bottom-up-algoritmer behandler hvert datapunkt som en enkelt klynge i starten og fusionerer derefter successivt (eller agglomererer) par klynger, indtil alle klynger er blevet fusioneret til en enkelt klynge, der indeholder alle datapunkter. Bottom-up hierarkisk klyngedannelse kaldes derfor hierarkisk agglomerativ klyngedannelse eller HAC. Dette hierarki af klynger er repræsenteret som et træ (eller dendrogram). Roden af træet er den unikke klynge, der samler alle prøverne, bladene er klynger med kun .n prøve., Tjek den grafiske fremstilling nedenfor for at se en illustration, før du går videre til den algoritme skridt

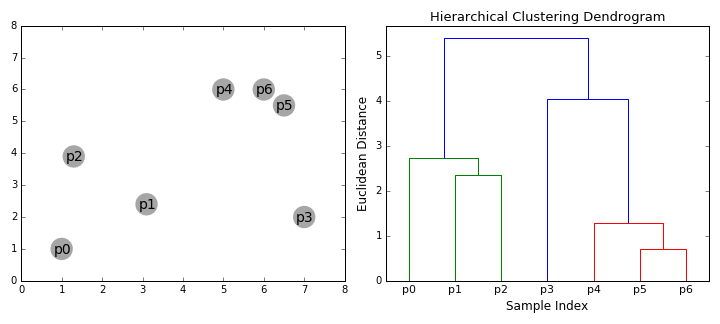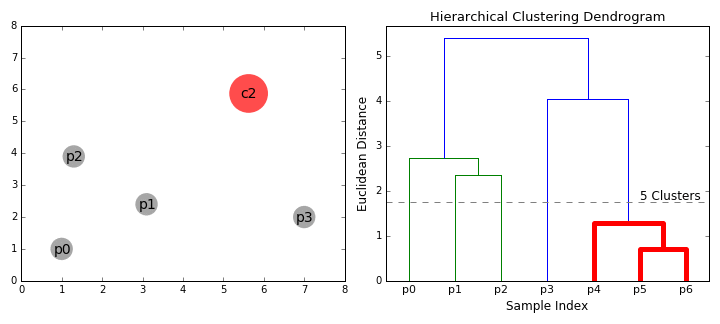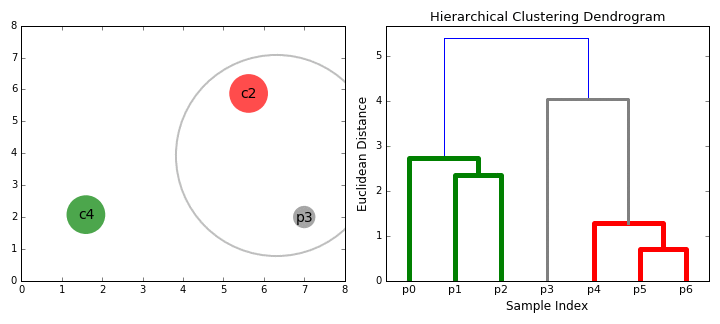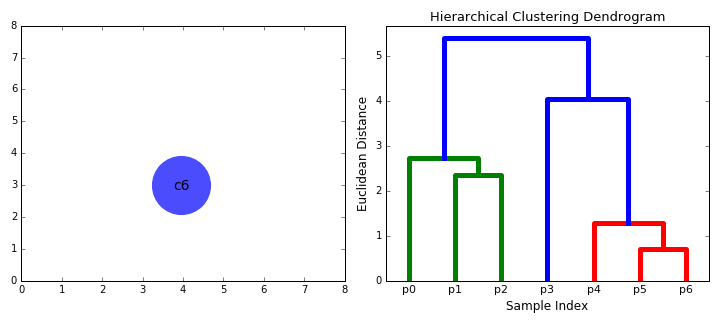
1. Vi begynde med at behandle hver enkelt datapunkt som en enkelt klynge jeg.e, hvis der er X data-punkter i vores datasæt, så vi har X klynger. Vi vælger derefter en afstandsmetrik, der måler afstanden mellem to klynger., Som et eksempel vil vi bruge gennemsnitlig kobling, der definerer afstanden mellem to klynger til at være den gennemsnitlige afstand mellem datapunkter i den første klynge og datapunkter i den anden klynge.
2. på hver iteration kombinerer vi to klynger i en. De to klynger, der skal kombineres, vælges som dem med den mindste gennemsnitlige kobling. Dvs. ifølge vores valgte afstandsmetrik har disse to klynger den mindste afstand mellem hinanden og er derfor de mest ens og bør kombineres.
3. Trin 2 gentages, indtil vi når roden af træet i.,e vi har kun en klynge, der indeholder alle datapunkter. På denne måde kan vi vælge, hvor mange klynger vi ønsker i sidste ende, blot ved at vælge, hvornår vi skal stoppe med at kombinere klyngerne, dvs.når vi holder op med at bygge træet!

hierarkisk klyngedannelse kræver ikke, at vi angiver antallet af klynger, og vi kan endda vælge, hvilket antal klynger der ser bedst ud, da vi bygger et træ. Derudover, algoritmen er ikke følsom over for valget af afstandsmetrik; alle har en tendens til at arbejde lige så godt, mens med andre klyngealgoritmer, valget af afstandsmetrik er kritisk., Et særligt godt brugstilfælde af hierarkiske klyngemetoder er, når de underliggende data har en hierarkisk struktur, og du vil gendanne hierarkiet; andre klyngealgoritmer kan ikke gøre dette. Disse fordele ved hierarkisk klyngedannelse kommer på bekostning af lavere effektivitet, da det har en tidskompleksitet på O(n3), i modsætning til den lineære kompleksitet af K-midler og GMM.