distributioner
kerneproblemet i hjertet af problemerne med Dirac-deltaet og lignende
matematiske objekter er problemet med differentierbarhed. Som Dirac anført i ovenstående citat, behøver du ikke rigtig løbe ind i problemer, hvis du bruger hans function funktion som en symbolsk regel for, hvordan det virker på andre funktioner, men han fortsætter med at differentiere in i hans beregninger, og det er her problemerne virkelig starte., Hvordan kan man først og fremmest vide “når disse operationer er tilladte”, når man ikke engang har en fast definition af objekterne, eller hvad det ville betyde at differentiere dem? Vi vil se, hvordan disse spørgsmål fører til afledning af nye og strengt definerede matematiske objekter.
funktionaler
overvej, hvordan man normalt bestemmer derivatet (eller antiderivative) af en funktion. Under normale omstændigheder har du med “klassiske” funktioner en veldefineret regel, der beskriver, hvordan en funktion kortlægger et sæt reelle tal til et andet sæt, siger f:…., I betragtning af dette og definitionerne af integralet eller derivatet kan man så tydeligt undersøge de værdier, som disse operatører giver, når de anvendes til funktionen. I tilfælde af δ har vi ingen brugbar definition til at fortsætte i disse linjer. I stedet er practice i praksis mest fremtrædende defineret af, hvordan det fungerer på andre veldefinerede funktioner (som i (3)). Dette er den centrale indsigt, der fører til den moderne teori om distributioner. Det viser sig, at den rigtige måde at matematisk behandle δ på og en stor klasse af lignende objekter er at stoppe med at forsøge at definere dem som funktioner overhovedet., Denne tankegang er godt beskrevet af Jean Dieudonne i sin anmeldelse af (se ):
… man begynder med en familie af meget “almindelige” funktioner (normalt med
forbindelse til differentieret egenskaber), der opfylder visse (normalt
integral) relationer, eller om der visse operationer er mulige; og
så opdager man, at en a priori større familie af funktioner, der opfylder
de samme forbindelser, eller kan blive udsat for lignende arbejde. Mange
spørgsmål kan så naturligvis stilles: er denne nye familie virkelig forskellig fra den første?, Hvis det er, hvad er forholdet mellem de to familier, og kan man give en præcis beskrivelse af den nye?
det er kun i den sidste fase af “forhistorien”, at det, der kan være
kaldet et revolutionerende synspunkt, vil dukke op med tanken om, at
Den “nye familie” muligvis består af andre objekter end funktioner.
de andre objekter, der henvises til, er funktionaler. Du kan tænke på en funktionel
som en funktion af funktioner., Da en funktion er en unik kortlægning fra et sæt
numre til et andet, kan en funktionel f defineres som en kortlægning F : C,,,
hvor C er et sæt funktioner. Det vil sige, en funktionel kort fungerer til reelle
numre., Et simpelt eksempel på en funktionel af denne type er det bestemte integral:

som klart tager en funktion f fra nogle sæt af passende integrable funktioner, og knytter det til et reelt tal, værdien af integralet, eller arealet under kurven f(x) mellem a og b. Dette er blot et enkelt eksempel., Man kan forestille sig et uendeligt antal funktionaler og sæt funktionaler; man kunne endda fortsætte med at generalisere og definere kortlægninger fra sæt funktionaler til reelle tal. Det er hverken her eller der. Det vigtige er, at det funktionelle koncept kan bruges til at definere distributioner.
sæt af testfunktioner
Vi kræver endnu en definition for at nå vores mål. Dette svarer til angivelse af sæt C af funktioner, hvorfra fordelingerne vil kortlægge funktioner til reelle tal., Funktioner indsamles ofte i sæt, der angiver deres grad af kontinuitet, differentierbarhed og kontinuiteten af deres derivater. Vi siger, at en funktion f er i sættet C ((skriv f) C)), hvis den er kontinuerlig over hele den virkelige linje i den forstand, at grænsen på alle punkter er den samme, når den tages fra venstre eller højre; det er ikke nødvendigvis differentierbart. Vi siger, at f C1 C1, hvis dets derivat eksisterer og er kontinuerligt, dvs. f’. C.. For eksempel er funktionen g (.)=|.| kontinuerlig, men ikke differentierbar ved 0= 0; g er i C but men ikke i C1., Vi kan generalisere dette og sige, at C is er det sæt funktioner, der for kontinuerlige funktioner har deres første n-derivater, hvor n er et heltal.
Når n bliver større, bliver sætene på en måde “mindre;” du kan altid finde funktioner (uendeligt mange!), der er i C but men ikke C 1 1. Disse “kontinuitetsrum” danner derfor en sekvens af indlejrede undergrupper, som afbildet nedenfor.

i bunden af denne uendelig sekvens af sæt af funktioner, som vi finde det sæt
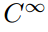
der er naturligvis mængden af alle funktioner, der har uendeligt mange kontinuerlig derivater. Mange kendte og venlige funktioner er i sidstnævnte klasse(f.eks. sin(sin); cos (;); e;; alle polynomier)., Disse funktioner kaldes “glat” eller “velopdragen”, fordi man kan udføre differentieringsoperationen på dem så mange gange som man glæder sig uden omhu. Men selvom dette sæt bestemt har uendeligt mange medlemmer, de er sjældne i den forstand, at de fleste funktioner ikke er så velopdragen.
det sæt, der er egnet til definitionen af distributioner er endnu mindre
end dette. Det kræver et yderligere kriterium: at funktionerne har kompakt støtte. Dette tekniske udtryk betyder simpelthen, at en funktion har ikke-nulværdier inden for et begrænset domæne og er ensartet nul uden for dette., Vi har derfor brug af notation
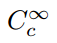
til at betegne det sæt af uendeligt løbende differentiable funktioner med kompakt støtte, og kalder disse funktioner test funktioner. For at definere en klasse af funktionaler, der bruger dette sæt som et domæne, skal vi være sikre på, at der faktisk er medlemmer af dette sæt., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

definitionen
fra dette punkt er definitionen af en distribution ligetil. En distribution er en lineær funktionel
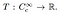
Det er, det er en kortlægning af en række test af funktioner til et reelt tal. Analogt med hvordan en bestemt funktion virker på et input nummer og producerer et output, specifikke distributioner er defineret ved, hvordan de omdanne test funktioner i tal., Fordelingen handler testfunktion φ kan skrives som T ()), eller almindeligvis som T T,…
man kan nu se, hvorfor distributioner kaldes generaliserede funktioner. For nogen
klassisk funktion som integrerende

er veldefineret, at der er en tilsvarende fordeling F, således at lang F,φ〉giver værdien af dette integral., Der er dog også distributioner, der ikke svarer til klassiske funktioner; distributioner er mere generelle. Som det burde være klart nu, den kanoniske eksempel på en fordeling, som ikke svarer til en klassisk funktion er Dirac.., Derfor er vi endelig ankommer til en helt stringent definition af δ fordelingen sådan, at

Den Generaliserede eller “Svage” Afledte
δ-distributionen er kun en af uendeligt mange distributioner, som ikke
svarer til den klassiske funktioner. Vi kan få nogle flere af disse ved at differentiere δ i betydningen distributioner., Men hvordan løser begrebet en
distribution problemet med differentiering som diskuteret tidligere? Vi behøver kun generalisere begrebet differentiering for at gælde for distributioner.
overvej en funktion f ∈ C1, så den kontinuerligt kan differentieres. Beregning ved hjælp af integration af dele, vi kan se, at

Udtrykket i parentes forsvinder da φ, som en test-funktion, har kompakt støtte., Dette generaliserer til en fordeling, siger, at F’, svarende til den funktion f’:

Denne beregning generaliserer helt nemt at distributioner, der ikke svarer til en klassisk funktionen f., På denne måde, kan vi definere den afledte T’ T i den forstand, at distributioner:

Dette er også nogle gange omtalt som svage derivat, da det udvider derivater til funktioner, der normalt ikke ville være differentiable. Dette generaliserer endnu mere, til højere ordens derivater., Vi kan definere den n ‘ te aedede af en fordeling T T⁽ⁿ⁾, hvor sidstnævnte er fordelingen sådan, at

Her,
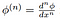
er klassisk derivat af test funktion, der er sikret
at eksistere ved den meget definition af test-funktioner!, Det følger heraf, at alle distributioner er uendeligt differentierbare (i form af distributioner).
dette fjerner helt den kamp, som Dirac og andre står over for, når man differentierer function-funktionen. Ved hvad vi har defineret her, et derivat af simply blot sifter for værdien af en anden funktioner derivat på nul., Formelt,

Dette giver en stringent matematisk ramme for derivater af δ, der dukkede op i den litteratur, længe før denne teori kom til eksistens.
Der er en række andre operationer, der gælder for funktioner, der er generaliseret til at gælde for distributioner. De kan tilføjes og trækkes fra, krammede, og forvandlet ved hjælp af Laplace og Fourier transformationer., Det er imidlertid umuligt at definere multiplikationen af distributioner på en måde, der bevarer algebraen, der gælder for klassiske funktioner (Sch .art.Umulighedssætningen).