Når en “normal” fraktion indeholder fraktioner i enten tælleren eller nævneren eller begge dele, betragter vi det som en kompleks fraktion. Denne type fraktion er også kendt som en sammensat fraktion.
Der er to metoder, der anvendes til at forenkle en sådan form for fraktion.
Metode 1
– Tasten trin:
- Opret en enkelt brøk, der i tælleren og nævneren.,
- Anvend delingsreglen for fraktioner ved at multiplicere tælleren med den gensidige eller inverse af nævneren.
- forenkle, hvis det er nødvendigt.
Metode 2
– Tasten trin:
- Finde den Mindste Fællesnævner (LCD) af alle nævnere i den sammensatte brøker.
- Multiplicer denne LCD til tælleren og nævneren for den komplekse fraktion.
- forenkle, hvis det er nødvendigt.,
efter at have gennemgået et par eksempler, skal du indse, at Metode 2 er meget bedre end Metode 1, fordi det næsten altid tager færre skridt for at komme til det endelige svar.
eksempler på, hvordan man forenkler komplekse fraktioner
eksempel 1: forenkle den komplekse fraktion nedenfor.
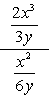
- ved Hjælp af Metode 1
Både tælleren og nævneren i den komplekse fraktion er allerede udtrykt som enkelt fraktioner. Det er fantastisk!,

næste trin for at gøre, er at anvende division regel, ved at gange tælleren med det reciprokke af nævneren. Afslut med at annullere fælles faktorer for at få det endelige svar.
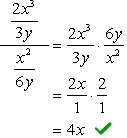
- ved Hjælp af Metode 2
Find LCD-af hele problemet er, at LCD-af top og bund nævnere.,

Siden af LCD-3y og 6y er bare \textbf{6y}, vil vi nu multiplicere komplekse tælleren og nævneren ved denne LCD. Derefter kan vi forvente, at problemet reduceres til en enkelt fraktion, som kan forenkles som normalt.
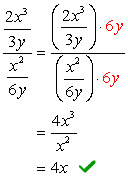
Eksempel 2: en Forenkling af det komplekse brøkdel nedenfor.,
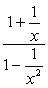
- ved Hjælp af Metode 1
I denne metode, vi ønsker at skabe en enkelt brøk, både i tæller og nævner. Naturligvis, dette problem ville kræve, at vi gør det først, før vi udfører division.
Tilføj fraktionerne i tælleren, og træk dem i nævneren.,
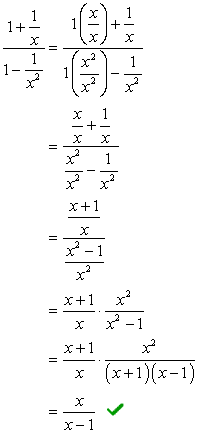
- ved Hjælp af Metode 2
Kigger på de nævnere \large{x} og \large{x^2}, dens LCD-skal være \large{x^2} Mangedoble top og bund af dette LCD.
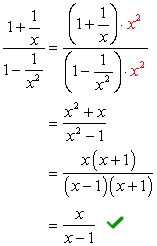
Eksempel 3: en Forenkling af det komplekse brøkdel nedenfor.,
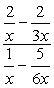
- ved Hjælp af Metode 1
Opret enkelt fraktioner i både tæller og nævner, og følg derefter ved at dividere brøker.
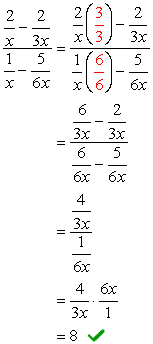
- ved Hjælp af Metode 2
Den samlede LCD-af terminologier er \color{red}6x. Brug dette til at formere sig gennem de øverste og nederste udtryk.,
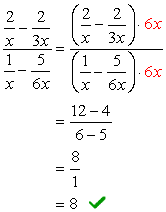
Eksempel 4: en Forenkling af det komplekse brøkdel nedenfor.
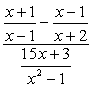
For dette problem, som vi kommer til at bruge Metode 1.
problemet kræver, at du anvender FOLIEMETODEN (multiplikation af to binomier) og en simpel faktorisering af trinomial. Det kan se lidt skræmmende i starten; men hvis du er opmærksom på detaljer, garanterer jeg dig, at det ikke er så slemt.,
Hvis du observerer, er den komplekse nævner allerede i den form, vi ønsker – med et fraktioneret symbol. Det betyder, at vi skal arbejde lidt på den komplekse tæller. Vores næste skridt ville være at omdanne den komplekse tæller til en “simpel” eller enkelt fraktion.
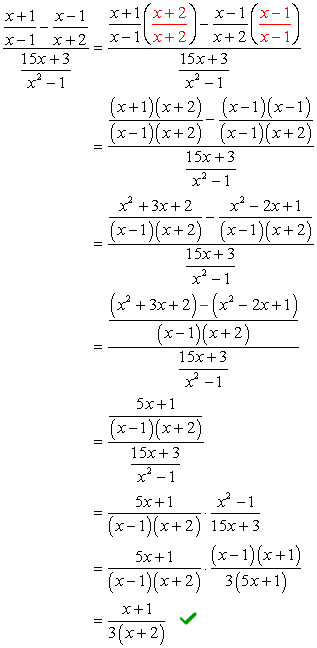
Eksempel 5: en Forenkling af det komplekse brøkdel nedenfor.
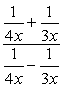
For dette problem, som vi kommer til at bruge Metode 2 kun.,
Vær opmærksom på, at LCD ‘ et for alle nævnerne kun er \color{red}12.. Brug dette som den fælles multiplikator for både top-og bundudtryk.
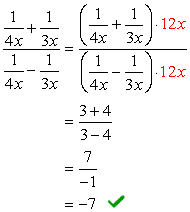
Praksis med Regneark
Du kan også være interesseret i:
at Multiplicere Komplekse Brøker
Dividere Komplekse Tal