Icosahedron (Dansk)

den almindelige icosahedron er en af de fem platoniske faste stoffer. Det er en konveks regelmæssig polyhedron består af tyve trekantede ansigter, med fem møde på hver af de tolv knudepunkter. Det har 30 kanter og 12 knudepunkter. Dens dobbelte polyhedron er dodecahedronen.,

Dimensioner

Hvis kant længde af en regelmæssig ikosaedret er , som den radius af en afgrænset sfære (en, der rører icosahedron på alle vertices) er

og den radius af en afmærket område (tangenten til hver af de icosahedron ansigter) er

mens den midradius, som berører midten af hver kant er

hvor 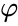(også kaldet ), det gyldne snit.,

Areal og volumen

overflade og volumen af en regelmæssig icosahedron af kant længde er:

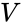
Kartesiske koordinater

følgende Retvinklede koordinater definere vertices af en icosahedron med kant-længde 2, centreret på oprindelse:

hvor er det gyldne snit (også skrevet τ)., Bemærk, at disse hjørner danner fem sæt af tre gensidigt centrerede, gensidigt ortogonale gyldne rektangler.

de 12 kanter af en almindelig oktaeder kan opdeles i det gyldne forhold, så de resulterende hjørner definerer en almindelig icosahedron. Dette gøres ved først at placere vektorer langs octahedron kanter, således at hvert ansigt er afgrænset af en cyklus, så er ligeledes partitionering hver kant i den gyldne middelvej langs retningen af dens vektor., De fem oktaeder, der definerer en given icosahedron, danner en regelmæssig polyhedral Forbindelse, ligesom de to icosahedra, der kan defineres på denne måde fra en given oktaeder.

Konstruktion af et system af equiangular linjer

følgende konstruktion af icoshaedron undgår kedelige beregninger i feltet nummer , der er nødvendige i mere elementære metoder.

eksistensen af icosahedronen svarer til eksistensen af seks lige linjer i., Faktisk skærer hinanden et sådant system af equiangular linjer med en Euklidisk sfære centreret på deres fælles skæringspunkt giver de tolv hjørner af en regelmæssig icosahedron som let kan kontrolleres. Omvendt antager eksistensen af en regelmæssig icosahedron, linjer defineret af dens seks par modsatte hjørner danner et e .uiangular system.

for at konstruere en equiangular system, vi starter med matrix

af pladsen størrelse ., (Huskeregel: matrix koder vinkler, akut for en positiv indlæg, stump anden måde, mellem fem cyklisk på hinanden følgende knuder støder op til en første vinkelspids af en icosahedron centreret i oprindelseslandet.)

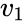
en ligetil beregning udbytter . Dette indebærer, at har egenværdier , begge med multiplicitet 3 siden er symmetrisk og af spor 0., Matrix inducerer thusan Euklidiske struktur på kvotienten plads , som er isomorf til siden kerne af har dimension 3. Billedet under fremskrivningen af de seks koordinat-akser i former således asystem af seks equiangular linjer i krydsende parvise på en fælles akut vinkel ., Ortogonale projektion af på -eigenspace af udbytter og dermed de tolv hjørner af ikosaedret.

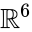
en anden ligetil konstruktion af icosahedronen bruger repræsentationsteori for den vekslende gruppe , der virker ved direkte isometrier på icosahedronen.

Stellationer

i henhold til specifikke regler defineret i bogen the fifty nine icosahedra blev 59 stellationer identificeret for den almindelige icosahedron. Den første form er selve icosahedronen., Den ene er en almindelig Kepler-Poinsot solid. Tre er regelmæssige sammensatte polyhedra.

21 af 59 stellations

ansigter ikosaedret udvidet, efterhånden som planer skærer hinanden, definition af regioner i rummet som det fremgår af dette stellation diagram af skæringspunkter i et enkelt plan.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Disse er invariant under de samme omdrejninger som den tetraeder, og er noget svarer til de irettesættelse terning og irettesættelse dodekaeder, herunder at visse former, der er chirale og nogle med Th-symmetri, altså have forskellige planer af symmetri fra tetraeder. Icosahedronen har et stort antal stellationer, herunder en af Kepler-Poinsot polyhedra og nogle af de regelmæssige forbindelser, som kunne diskuteres her.

icosahedronen er unik blandt de platoniske faste stoffer ved at have en dihedral vinkel på ikke mindre end 120.. Dens dihedrale vinkel er cirka 138.19..,ss end 120° og kan ikke bruges som den står over for en konveks regulære polyeder, fordi en sådan konstruktion ikke opfylder kravet om, at mindst tre ansigter mødes på en vinkelspids og efterlade en positiv defekt til at folde den sammen i tre dimensioner, icosahedra kan ikke bruges som cellerne i en konveks regelmæssig polychoron fordi, på samme måde, mindst tre celler, der skal mødes på en kant og efterlade en positiv defekt for at folde i fire dimensioner (generelt for en konveks polytope i dimensioner, mindst tre facetter, der skal mødes i en spids og efterlade en positiv defekt for at folde i n-space)., Når det kombineres med egnede celler med mindre dihedrale vinkler, kan icosahedra imidlertid bruges som celler i semi-regelmæssig polychora (for eksempel snub 24-cellen), ligesom sekskanter kan bruges som ansigter i semi-regelmæssig polyhedra (for eksempel den afkortede icosahedron). Endelig bærer ikke-konvekse polytoper ikke de samme strenge krav som konvekse polytoper, og icosahedra er faktisk cellerne i icosahedral 120-cellen, en af de ti ikke-konvekse regelmæssige polychora.

en icosahedron kan også kaldes et gyroelangstrakt femkantet bipyramid., Det kan nedbrydes til en gyroelang femkantet pyramide og en femkantet pyramide eller i en femkantet antiprisme og to lige femkantede pyramider.

icosahedronen kan også kaldes en snub tetrahedron, da snubificering af en regelmæssig tetrahedron giver en regelmæssig icosahedron., Alternativt til at bruge den fælles nomenklatur for irettesættelse polyedre, der refererer til en irettesættelse terning som en irettesættelse cuboctahedron (cuboctahedron = udbedret terning) og en irettesættelse dodekaeder som en irettesættelse icosidodecahedron (icosidodecahedron = udbedret dodekaeder), man kan kalde ikosaedret de irettesættelse octahedron (octahedron = udbedret tetraeder).

en korrigeret icosahedron danner en icosidodecahedron.

Icosahedron vs dodecahedron

Når en icosahedron er indskrevet i en kugle, optager den mindre af kuglens volumen (60.54%) end en dodecahedron indskrevet i samme kugle (66.49%).,

da disse er dualer, er det også muligt at omdanne den ene til den anden(se nedenfor).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	i nogle rollespil bruges den tyve-sidede die (for kort, d20) til at bestemme succes eller fiasko af en handling. Denne dør er i form af en regelmæssig icosahedron. Det kan være nummereret fra “0” til “9” to gange (i hvilken form det normalt tjener som en ti-sidet matrice eller d10), men de fleste moderne versioner er mærket fra “1” til “20”. Se D20 System.,

En icosahedron er den tre-dimensionelle spil bestyrelsen for Icosagame, tidligere kendt som Ico Crystal Spil.

en icosahedron bruges i brætspil Scattergories at vælge et bogstav i alfabetet. Seks små brugte bogstaver, såsom X,, og Z, udelades.

inde i en magisk 8-Ball udskrives forskellige svar på ja-nej-spørgsmål på en almindelig icosahedron.

icosahedronen, der vises i en funktionel form, ses i Sol De la Flor-lysskyggen., Rosetten dannet af de overlappende stykker viser en lighed med Frangipani-blomsten.

Hvis hver kant af en icosahedron erstattes af en en ohm modstand, modstanden mellem modsatte knudepunkter er 0,5 ohm, og at mellem tilstødende knudepunkter 11/30 ohm.

symmetrigruppen af icosahedronen er isomorf til den vekslende gruppe på fem bogstaver. Denne nonabelian simple gruppe er den eneste nontrivial normal undergruppe af den symmetriske gruppe på fem bogstaver., Da Galois gruppen af de generelle quintic ligning er isomorf til den symmetriske gruppe på fem bogstaver, og det faktum, at ikosaedriske gruppe er enkel og nonabelian betyder, at quintic ligninger behøver ikke at have en løsning i radikaler. Beviset for Abel-Ruffini sætning bruger denne simple kendsgerning, og Feli.Klein skrev en bog, der gjorde brug af teorien om icosahedral symmetries at udlede en analytisk løsning på den generelle quinuintic ligning.,

Se også

Skabelon:Wiktionarypar

• Afkortet icosahedron
• Regulære polyeder
• Geodætiske net bruge et iterativt gennemskæres icosahedron til at generere net på en kugle
• Jessen ‘ s icosahedron

Skabelon:Wikisource1911Enc

Skabelon:Commonscat

• Weisstein, Eric W., “Icosahedron” fra MathWorld.
• papirmodeller af icosahedronen
• den ensartede Polyhedra
• K. J. M., MacLean, En Geometrisk Analyse af de Fem Platoniske Legemer og Andre Semi-Regulære Polyedre
• Interaktive Icosahedron model – virker ret i din web-browser
• Virtual Reality Polyedre redigeret af Polyedre
• Tulane.,edu er En diskussion af de super struktur og ikosaedret
• Papir Modeller af Polyedre Mange links
• Origami Polyedre – Modeller er lavet med en Modular Origami
• video af ikosaedriske spejl er en skulptur

Skabelon:Polyedre

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri jeg rregulltsr:Икосаедарsv:Ikosaederta:brød ud முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.