LEONARDO FIBONACCI – ITALIENSK MATEMATIKER, (SKREV LEBER ABACI)

Leonardo af Pisa (Fibonacci) c.1170-1250)

Det 13 Århundrede italienske Leonardo af Pisa, bedre kendt under sit øgenavn Fibonacci, var måske den mest talentfulde Vestlige matematiker fra middelalderen. Lidt er kendt af hans liv, bortset fra at han var søn af en told offical og som barn, han rejste rundt i Nordafrika med sin far, hvor han lærte om arabisk matematik., På hans tilbagevenden til Italien, han bidraget til at formidle denne viden i hele Europa, og dermed sætte i gang en foryngelse i europæisk matematik, som havde ligget i vid udstrækning sovende i århundreder i den mørke middelalder.

især i 1202 skrev han et enormt indflydelsesrige bog, som hedder “Liber Abaci” (“Book of Beregning”), som arbejdede han for at fremme brugen af de Hindu-arabiske talsystem, der beskriver dens mange fordele for virksomhederne og matematikere både over klodset system af Romertal derefter i brug i Europa., På trods af sine åbenlyse fordele, udnyttelsen af systemet i Europa var langsom (det var trods alt under Korstogene mod Islam, en tid, hvor noget arabisk, blev betragtet med stor mistænksomhed), og arabertal var endda forbudt i byen Firenze i 1299 under påskud af, at de var lettere at forfalske end Romertal. Imidlertid, sund fornuft sejrede til sidst, og det nye system blev vedtaget i hele Europa i det 15.århundrede, gør det romerske system forældet., Den vandrette bjælke notation for fraktioner blev også første gang brugt i dette arbejde (selv efter arabisk praksis med at placere den brøkdel til venstre for heltal).

Fibonacci-Sekvens

opdagelsen af de berømte Fibonacci-sekvens

Fibonacci er bedst kendt, men hans introduktion i Europa af et bestemt antal, rækkefølge, som siden er blevet kendt som Fibonacci-Tal eller Fibonacci-Sekvens., Han opdagede sekvensen – den første rekursive talsekvens kendt i Europa – mens han overvejede et praktisk problem i “Liber Abaci”, der involverede væksten i en hypotetisk population af kaniner baseret på idealiserede antagelser. Han bemærkede, at efter hver måneds generation, antallet af par af kaniner, er steget fra 1 til 2 til 3 til 5 og 8 til 13, osv., og som er identificeret, hvordan sekvens skred ved at lægge de to foregående tal (i matematiske termer, Fn = Fn-1 + Fn-2), en sekvens, der kunne i teorien udvides i det uendelige.,sekvensen, som faktisk havde været kendt af indiske matematikere siden det 6.århundrede, har mange interessante matematiske egenskaber, og mange af sekvensens implikationer og forhold blev først opdaget flere århundreder efter Fibonacci ‘ s død., For eksempel, den sekvens regenererer sig selv i nogle overraskende måder: hver tredje F-tal er deleligt med 2 (F3 = 2), hver fjerde F-tal er deleligt med 3 (F4 = 3), hver femte F-tal er deleligt med 5 (F5 = 5), hver sjette F-tal er deleligt med 8 (F6 = 8), hver syvende F-tal er deleligt med 13 (F7 = 13), osv., Antallet af sekvensen har også vist sig at være allestedsnærværende i naturen: blandt andet har mange arter af blomstrende planter antal kronblade i Fibonacci-sekvensen; spiralarrangementerne af ananas forekommer i 5s og 8s, pinecones i 8s og 13s, og frøene af solsikkehoveder i 21s, 34s, 55s eller endnu højere termer i sekvensen; etc.,

Den Gyldne snit φ

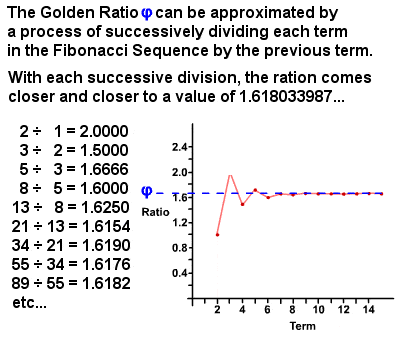
Det Gyldne snit φ kan være afledt af Fibonacci-Sekvens

I 1750’erne, Robert Simson bemærkes, at andelen af hver valgperiode i Fibonacci-Sekvens til den foregående periode tilgange, med stadig større nøjagtighed den højere form, en ratio på ca 1 : 1.6180339887 (det er faktisk en irrationel antal svarende til (1 + √5)⁄2, som siden er blevet beregnet til tusindvis af decimaler)., Denne værdi betegnes som det gyldne forhold, også kendt som det gyldne middel, gyldne snit, guddommelige forhold osv., og betegnes normalt med det græske bogstav phi φ (eller undertiden stort bogstav Phi Φ). I det væsentlige er to mængder i det gyldne forhold, hvis forholdet mellem summen af mængderne og den større mængde er lig med forholdet mellem den større mængde og den mindre. Det gyldne forhold i sig selv har mange unikke egenskaber, såsom 1 = = = – – 1 (0.618…) og22 = + + 1 (2.618…), og der er utallige eksempler på det, der findes både i naturen og i den menneskelige verden.,

Et rektangel med sider i forholdet 1 : φ er kendt som et Gyldent Rektangel, og mange kunstnere og arkitekter i hele historie (helt tilbage til det gamle Egypten og Grækenland, men især populær i Renæssancen kunst af Leonardo da Vinci og hans samtidige) har proportioneret deres værker omkring ved hjælp af det Gyldne snit og Gyldne Rektangler, som er almindeligt anset for at være medfødt æstetisk tiltalende. En bue, der forbinder modsatte punkter af stadig mindre indlejrede gyldne rektangler, danner en logaritmisk spiral, kendt som en gylden Spiral., Det gyldne forhold og Den Gyldne Spiral kan også findes i et overraskende antal tilfælde i naturen, fra skaller til blomster til dyrehorn til menneskelige kroppe til stormsystemer til komplette galakser.,

Det skal blive husket, dog, at Fibonacci-Sekvens, der var faktisk kun en meget lille del i “Liber Abaci” – ja, den sekvens kun modtaget Fibonacci ‘ s navn i 1877, når Eduouard Lucas besluttede sig for at hylde ham ved at navngive serien efter ham – og at Fibonacci selv var ikke ansvarlig for at identificere nogen af de interessante matematiske egenskaber af den sekvens, dens forhold til den Gyldne middelvej og Gyldne Rektangler og Spiraler osv.,

Gitter Multiplikation

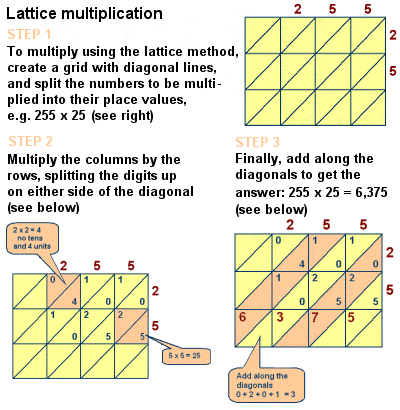
Fibonacci indført gitter multiplikation at Europa

Men bogen indflydelse på middelalderlige matematik er ubestridelige, og det gør også at omfatte drøftelser af en række andre matematiske problemer, såsom den Kinesiske Resten Sætning, perfekt tal og primtal, formler for aritmetisk række, og for firkantet pyramide numre, Euklidisk geometriske beviser, og en undersøgelse af samtidige ligninger langs linjer diofant og Al-Karaji., Han beskrev også gitter (eller sigte) multiplikationsmetode til multiplikation af store tal, en metode – oprindeligt banebrydende af islamiske matematikere som Al-KH .ari .mi – algoritmisk svarende til lang multiplikation.

hverken var “Liber Abaci” Fibonacci eneste bog, selv om det var hans vigtigste., Hans “Liber Quadratorum” (“The Book of Squares”), for eksempel, er en bog om algebra, offentliggjort i 1225, hvor der vises en opgørelse over, hvad der nu kaldes Fibonacci ‘ s identitet – nogle gange også kendt som Brahmagupta identitet efter den meget tidligere Indiske matematiker, som også kom til den samme konklusion – at produktet af to summer af to firkanter er i sig selv en sum af to kvadrater fx (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,