Læringsresultater
- Bliv fortrolig med historien om positionelle antal systemer
- Identificere baser, der har været anvendt i mange systemer historisk
- Konverterer tal mellem baserne
- Bruge to forskellige metoder for at konvertere tal mellem baser
Baggrund
Som du måske forestiller dig, udvikling af en base-system er et vigtigt skridt i at gøre optælling proces mere effektiv., Vores eget base-ten-system stammer sandsynligvis fra det faktum, at vi har 10 fingre (inklusive tommelfingre) på to hænder. Dette er en naturlig udvikling. Andre civilisationer har imidlertid haft en række andre baser end ti. For eksempel brugte de indfødte i Queueensland et base-to-system, der tæller som følger: “en, to, to og en, to to, meget.”Nogle moderne sydamerikanske stammer har et base-fem system, der tæller på denne måde:” en, to, tre, fire, hånd, hånd og en, hånd og to ” og så videre. Babylonierne brugte en base-tres (se .igesimal) system., I dette kapitel pakker vi op med et specifikt eksempel på en civilisation, der faktisk brugte et andet basissystem end 10.
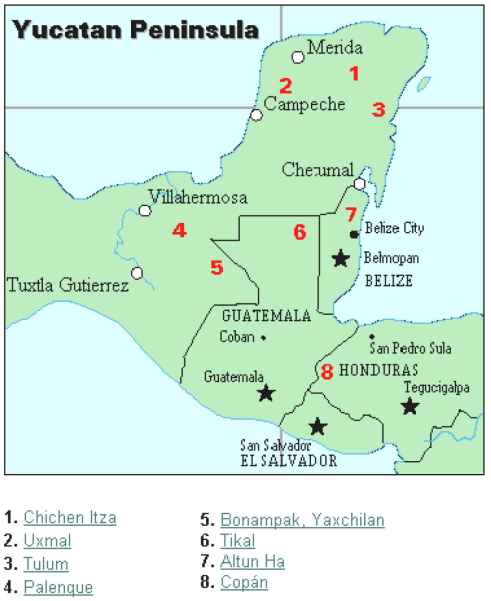 mayaernes civilisation er generelt dateret fra 1500 fvt til 1700 CE. Yucatan-halvøen (se figur 16) I Me .ico var scenen for udviklingen af en af de mest avancerede civilisationer i den antikke verden. Mayaerne havde et sofistikeret rituelt system, der blev overvåget af en præsteklasse. Denne klasse af præster udviklede en filosofi med tiden som guddommelig og evig., Kalenderen og beregningerne i forbindelse hermed var således meget vigtige for præsteklassens rituelle liv og dermed Maya-folket. Faktisk kommer meget af det, vi ved om denne kultur, fra deres kalenderregistre og astronomidata. En anden vigtig kilde til information om mayaerne er skrifterne fra Far Diego de Landa, der rejste til Me .ico som missionær i 1549.
mayaernes civilisation er generelt dateret fra 1500 fvt til 1700 CE. Yucatan-halvøen (se figur 16) I Me .ico var scenen for udviklingen af en af de mest avancerede civilisationer i den antikke verden. Mayaerne havde et sofistikeret rituelt system, der blev overvåget af en præsteklasse. Denne klasse af præster udviklede en filosofi med tiden som guddommelig og evig., Kalenderen og beregningerne i forbindelse hermed var således meget vigtige for præsteklassens rituelle liv og dermed Maya-folket. Faktisk kommer meget af det, vi ved om denne kultur, fra deres kalenderregistre og astronomidata. En anden vigtig kilde til information om mayaerne er skrifterne fra Far Diego de Landa, der rejste til Me .ico som missionær i 1549.
 der var to talsystemer udviklet af mayaerne—et for det almindelige folk og et for præsterne., Ikke kun brugte disse to systemer forskellige symboler, de brugte også forskellige basesystemer. For præsterne blev talesystemet styret af ritual. Årets dage blev anset for at være guder, så de formelle symboler for dagene var dekorerede Hoveder, ligesom prøven til venstre siden den grundlæggende kalender var baseret på 360 dage, anvendte præstens talsystem et blandet basissystem med multipler på 20 og 360. Dette skaber et forvirrende system, hvis detaljer vi vil springe over.,/td>
der var to talsystemer udviklet af mayaerne—et for det almindelige folk og et for præsterne., Ikke kun brugte disse to systemer forskellige symboler, de brugte også forskellige basesystemer. For præsterne blev talesystemet styret af ritual. Årets dage blev anset for at være guder, så de formelle symboler for dagene var dekorerede Hoveder, ligesom prøven til venstre siden den grundlæggende kalender var baseret på 360 dage, anvendte præstens talsystem et blandet basissystem med multipler på 20 og 360. Dette skaber et forvirrende system, hvis detaljer vi vil springe over.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system., Som vi sagde tidligere, brugte mayaerne et base-20-system, kaldet” vigesimal ” – systemet. Ligesom vores system er det positionelt, hvilket betyder, at placeringen af et numerisk symbol angiver dets stedværdi. I den følgende tabel kan du se stedværdien i dets lodrette format.
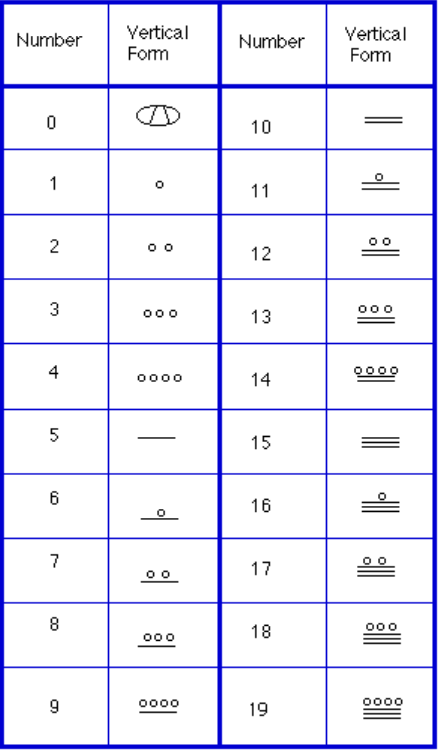
for at skrive tal ned var der kun tre symboler nødvendige i dette system. En vandret bjælke repræsenterede mængden 5, en prik repræsenterede mængden 1, og et særligt symbol (menes at være en skal) repræsenterede nul., Maya – systemet kan have været den første til at gøre brug af nul som pladsholder/nummer. De første 20 numre vises i tabellen til højre.i modsætning til vores system, hvor stedet starter til højre og derefter bevæger sig til venstre, placerer Maya-systemerne dem i bunden af en lodret orientering og bevæger sig op, når stedværdien stiger.
Når tal er skrevet i lodret form, bør der aldrig være mere end fire prikker på et enkelt sted. Når du skriver Maya-numre, bliver hver gruppe på fem prikker en bjælke., Også, der bør aldrig være mere end tre søjler på et enkelt sted…fire søjler ville blive konverteret til en prik på det næste sted op. Det er det samme som 10 at blive konverteret til en 1 på det næste sted, når vi bærer under tilføjelse.
eksempel
Hvad er værdien af dette tal, som vises i lodret form?
Eksempel
Hvad er værdien af følgende Maya-nummer?,
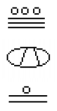
prøv det
konverter Maya-nummeret nedenfor til base 10.,

Eksempel
Konvertere base 10 antal 357510 til Maya-tal.
skrivning af tal med baser større end 10
Når basen på et tal er større end 10, adskilles hvert “ciffer” med et komma for at gøre adskillelsen af cifre klar.
for eksempel i base 20 for at skrive det nummer, der svarer til 17 × 202 + 6 × 201 + 13 × 200, vi ville skrive 17.61320.
i den følgende video præsenterer vi flere eksempler på, hvordan man skriver tal ved hjælp af Maya-tal samt konverterer tal skrevet i Maya til i base 10-form.,
Den næste video viser flere eksempler på at konvertere base 10-Tal til Maya-tal.
tilføjelse af Mayan-numre
Når vi tilføjer Mayan-numre sammen, vedtager vi en ordning, som mayaerne sandsynligvis ikke brugte, men som vil gøre livet lidt lettere for os.
Eksempel
Tilføje, i Maya, nummer 37 og 29:

Prøv Det
Prøv at tilføje 174 og 78 i Maya-ved først at konvertere til Maya-numre og derefter arbejder udelukkende inden for dette system. Tilføj ikke i base-ti (decimal) indtil slutningen, når du tjekker dit arbejde.
I den sidste video viser vi flere eksempler på at tilføje Maya-tal.,
i dette modul har vi kort skitseret udviklingen af tal og vores tællesystem med vægt på den “korte” del. Der er mange kilder til information og forskning, der fylder mange mængder bøger om dette emne. Desværre kan vi ikke begynde at komme tæt på at dække alle de oplysninger, der er derude.

Vi har kun ridset overfladen af det væld af forskning og information, der findes om udviklingen af tal og tælling gennem menneskets historie., Det, der er vigtigt at bemærke, er, at det system, vi bruger hver dag, er et produkt af tusinder af års fremskridt og udvikling. Det repræsenterer bidrag fra mange civilisationer og kulturer. Det kommer ikke ned til os fra himlen, en gave fra guderne. Det er ikke oprettelsen af en lærebog udgiver. Det er faktisk så menneskeligt som vi er, ligesom resten af matematikken. Bag hvert symbol, formel og regel er der et menneskeligt ansigt, der findes eller i det mindste søges.
desuden håber vi, at du nu har en grundlæggende forståelse for, hvor interessante og forskellige talesystemer kan få., Også, vi er ret sikker på, at du også er begyndt at erkende, at vi tager vores eget nummer system for givet så meget, at når vi forsøger at tilpasse sig til andre systemer eller baser, vi befinder os virkelig skulle koncentrere sig og tænke over, hvad der foregår.







