Die 5 Clustering-Algorithmen-Daten-Wissenschaftler Müssen Wissen,

ich habe vor kurzem angefangen ein Buch mit gezielten Bildungs-newsletter. Book Dives ist ein zweiwöchiger Newsletter, in dem wir für jede neue Ausgabe in ein Sachbuch eintauchen. Sie erfahren mehr über die Kernlektionen des Buches und wie Sie sie im wirklichen Leben anwenden können. Sie können es hier abonnieren.

Clustering ist eine Technik des maschinellen Lernens, bei der Datenpunkte gruppiert werden. Bei einer Reihe von Datenpunkten können wir einen Clustering-Algorithmus verwenden, um jeden Datenpunkt in eine bestimmte Gruppe zu klassifizieren., Theoretisch sollten Datenpunkte, die sich in derselben Gruppe befinden, ähnliche Eigenschaften und/oder Merkmale aufweisen, während Datenpunkte in verschiedenen Gruppen sehr unterschiedliche Eigenschaften und/oder Merkmale aufweisen sollten. Clustering ist eine Methode des unbeaufsichtigten Lernens und eine gängige Technik für die statistische Datenanalyse, die in vielen Bereichen verwendet wird.

In der Datenwissenschaft können wir mithilfe der Clusteranalyse wertvolle Erkenntnisse aus unseren Daten gewinnen, indem wir sehen, in welche Gruppen die Datenpunkte fallen, wenn wir einen Clusteralgorithmus anwenden., Heute werden wir uns 5 beliebte Clustering-Algorithmen ansehen, die Datenwissenschaftler kennen müssen, und ihre Vor-und Nachteile!

K-Means Clustering

K-Means ist wahrscheinlich der bekannteste Clustering-Algorithmus. Es wird in vielen einführenden Data Science-und Machine Learning-Klassen unterrichtet. Es ist leicht zu verstehen und in Code zu implementieren! Schauen Sie sich die Grafik unten für eine illustration.,

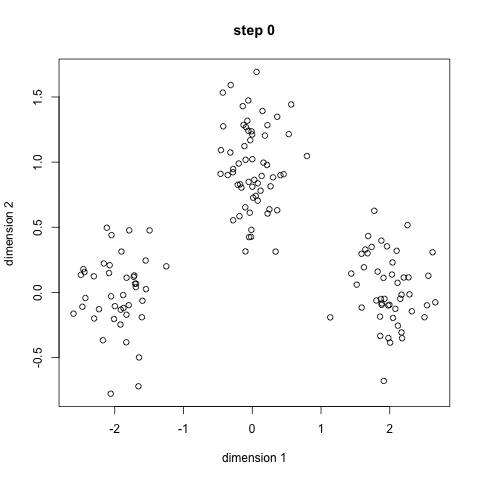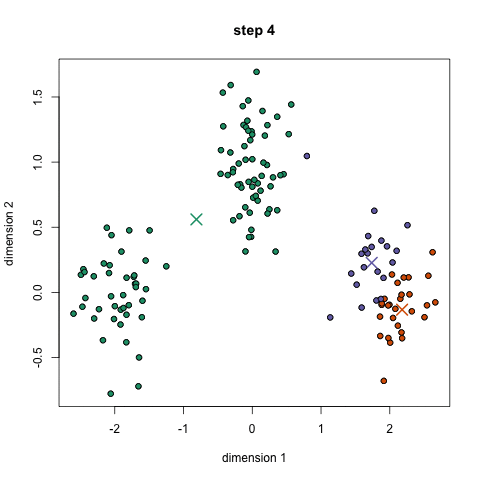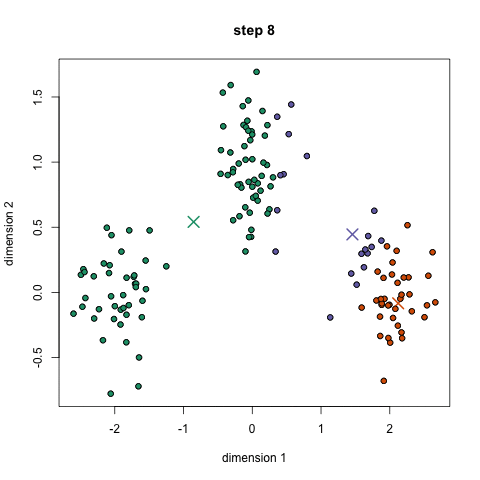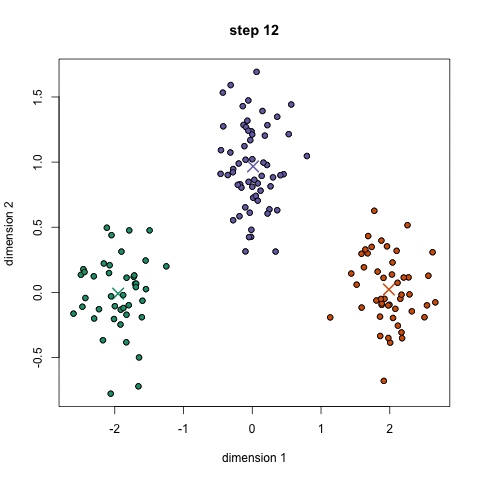
1. Um zu beginnen, wir wählen zuerst eine Reihe von Klassen/Gruppen aus, die verwendet werden sollen, und initialisieren zufällig ihre jeweiligen Mittelpunkte. Um die Anzahl der zu verwendenden Klassen herauszufinden, sollten Sie sich die Daten kurz ansehen und versuchen, unterschiedliche Gruppierungen zu identifizieren. Die Mittelpunkte sind Vektoren gleicher Länge wie jeder Datenpunktvektor und sind die „X ‚ s“ in der obigen Grafik.,
2. Jeder Datenpunkt wird klassifiziert, indem der Abstand zwischen diesem Punkt und jedem Gruppenzentrum berechnet und dann der Punkt klassifiziert wird, der sich in der Gruppe befindet, deren Mittelpunkt ihm am nächsten liegt.
3. Basierend auf diesen klassifizierten Punkten berechnen wir das Gruppenzentrum neu, indem wir den Mittelwert aller Vektoren in der Gruppe verwenden.
4. Wiederholen Sie diese Schritte für eine festgelegte Anzahl von Iterationen oder bis sich die Gruppenzentren zwischen den Iterationen nicht wesentlich ändern. Sie können sich auch dafür entscheiden, die Gruppencenter einige Male zufällig zu initialisieren und dann den Lauf auszuwählen, der so aussieht, als ob er die besten Ergebnisse liefert.,

K-Means hat den Vorteil, dass es ziemlich schnell ist, da wir nur die Abstände zwischen Punkten und Gruppenzentren berechnen. sehr wenige Berechnungen! Es hat somit eine lineare Komplexität O(n).

Andererseits hat K-Means einige Nachteile. Zunächst müssen Sie auswählen, wie viele Gruppen / Klassen es gibt. Dies ist nicht immer trivial und idealerweise möchten wir mit einem Clustering-Algorithmus, dass er diese für uns herausfindet, da es darum geht, einen Einblick in die Daten zu gewinnen., K-means beginnt auch mit einer zufälligen Auswahl von Clusterzentren und kann daher bei verschiedenen Durchläufen des Algorithmus unterschiedliche Clusterergebnisse liefern. Daher sind die Ergebnisse möglicherweise nicht wiederholbar und es fehlt an Konsistenz. Andere Clustermethoden sind konsistenter.

K-Medians ist ein weiterer Clustering-Algorithmus, der sich auf K-Means bezieht, außer anstatt die Gruppenmittelpunkte mit dem Mittelwert neu zu berechnen, verwenden wir den Medianvektor der Gruppe., Diese Methode reagiert weniger empfindlich auf Ausreißer (aufgrund der Verwendung des Medians), ist jedoch bei größeren Datensätzen viel langsamer, da bei jeder Iteration beim Berechnen des Medianvektors eine Sortierung erforderlich ist.

Mean-Shift-Clustering

Mean-Shift-Clustering ist ein gleitfensterbasierter Algorithmus, der versucht, dichte Bereiche von Datenpunkten zu finden. Es ist ein Zentroid-basierter Algorithmus, was bedeutet, dass das Ziel darin besteht, die Mittelpunkte jeder Gruppe/Klasse zu lokalisieren, indem Kandidaten für Mittelpunkte aktualisiert werden, um der Mittelwert der Punkte innerhalb des Schiebefensters zu sein., Diese Kandidatenfenster werden dann in einer Nachbearbeitungsstufe gefiltert, um nahezu Duplikate zu eliminieren und bilden den endgültigen Satz von Mittelpunkt und ihre entsprechenden Gruppen. Schauen Sie sich die Grafik unten für eine illustration.

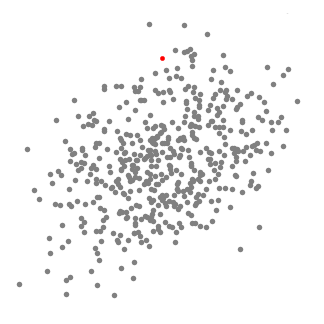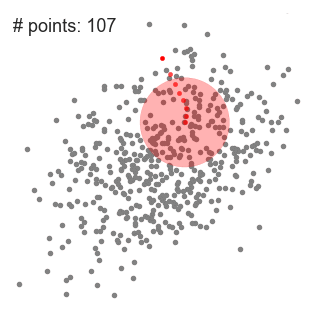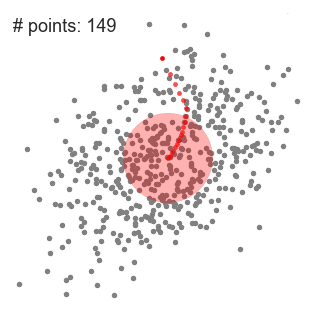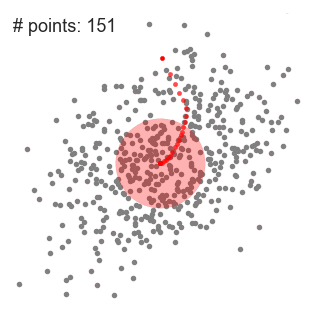
1. Zu erklären, mean-shift betrachten wir die Menge der Punkte im zweidimensionalen Raum wie in der obigen Abbildung., Wir beginnen mit einem kreisförmigen Schiebefenster, das an einem Punkt C zentriert ist (zufällig ausgewählt) und den Radius r als Kern hat. Mean Shift ist ein Bergsteigeralgorithmus, bei dem dieser Kernel bei jedem Schritt bis zur Konvergenz iterativ in einen Bereich höherer Dichte verschoben wird.
2. Bei jeder Iteration wird das Schiebefenster in Richtung Regionen höherer Dichte verschoben, indem der Mittelpunkt auf den Mittelwert der Punkte innerhalb des Fensters verschoben wird (daher der Name). Die Dichte innerhalb des Schiebefensters ist proportional zur Anzahl der Punkte darin., Natürlich bewegt es sich durch Verschieben auf den Mittelwert der Punkte im Fenster allmählich in Richtung Bereiche höherer Punktdichte.
3. Wir verschieben das Schiebefenster weiter nach dem Mittelwert, bis es keine Richtung gibt, in der eine Verschiebung mehr Punkte innerhalb des Kernels aufnehmen kann. Schauen Sie sich die obige Grafik an; Wir bewegen den Kreis so lange, bis wir die Dichte nicht mehr erhöhen (dh die Anzahl der Punkte im Fenster).
4. Dieser Vorgang der Schritte 1 bis 3 erfolgt mit vielen Schiebefenstern, bis alle Punkte innerhalb eines Fensters liegen., Wenn sich mehrere Schiebefenster überlappen, bleibt das Fenster mit den meisten Punkten erhalten. Die Datenpunkte werden dann entsprechend dem Schiebefenster gruppiert, in dem sie sich befinden.

Eine Abbildung des gesamten Prozesses von Ende zu Ende mit allen Schiebefenstern ist unten dargestellt. Jeder schwarze Punkt repräsentiert den Schwerpunkt eines Schiebefensters und jeder graue Punkt ist ein Datenpunkt.,

Im Gegensatz für K-Means-Clustering ist es nicht erforderlich, die Anzahl der Cluster auszuwählen, da mean-shift dies automatisch erkennt. Das ist ein massiver Vorteil. Die Tatsache, dass die Clusterzentren zu den Punkten maximaler Dichte konvergieren, ist ebenfalls sehr wünschenswert, da es sehr intuitiv zu verstehen ist und in einem natürlich datengesteuerten Sinne gut passt., Der Nachteil ist, dass die Auswahl der Fenstergröße/des Radius „r“ nicht trivial sein kann.

Dichtebasiertes räumliches Clustering von Anwendungen mit Rauschen (DBSCAN)

DBSCAN ist ein dichtebasierter Clusteralgorithmus, der der Mittelverschiebung ähnelt, jedoch einige bemerkenswerte Vorteile bietet. Schauen Sie sich unten eine weitere ausgefallene Grafik an und fangen wir an!,

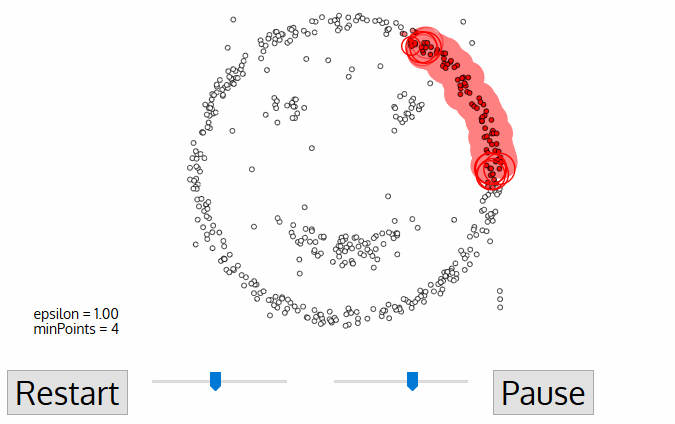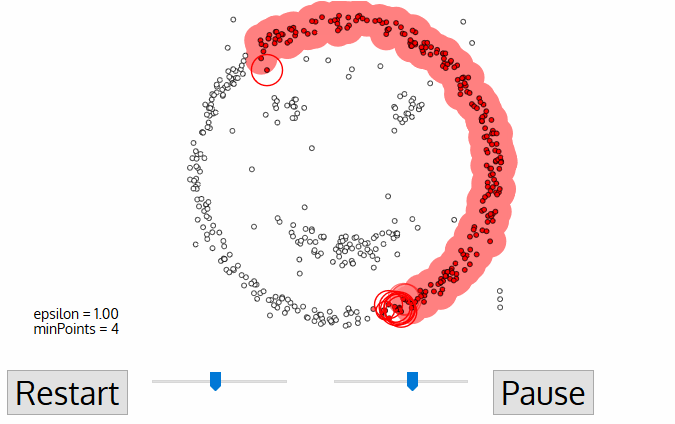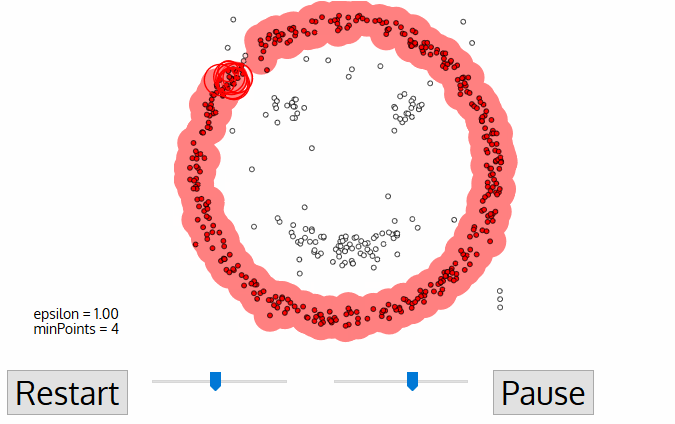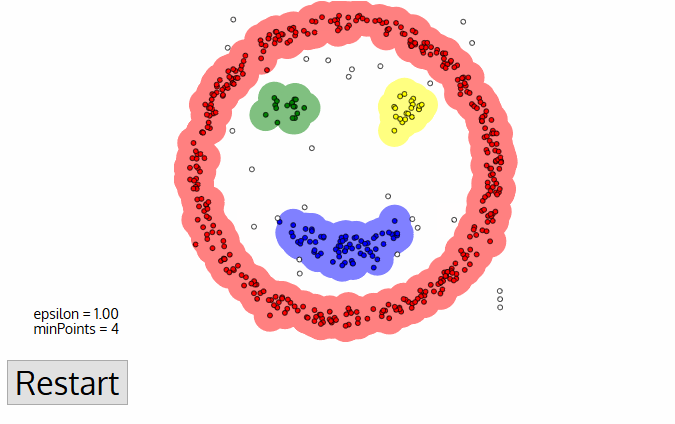
1. DBSCAN beginnt mit einem beliebigen Start-Daten zeigen, dass noch nicht besucht wurden. Die Nachbarschaft dieses Punktes wird unter Verwendung eines Abstands Epsilon ε extrahiert (Alle Punkte, die innerhalb der ε-Entfernung liegen, sind Nachbarschaftspunkte).,
2. Wenn innerhalb dieser Nachbarschaft eine ausreichende Anzahl von Punkten (gemäß minPoints) vorhanden ist, beginnt der Clustering-Prozess und der aktuelle Datenpunkt wird zum ersten Punkt im neuen Cluster. Andernfalls wird der Punkt als Rauschen gekennzeichnet (später könnte dieser verrauschte Punkt Teil des Clusters werden). In beiden Fällen wird dieser Punkt als „besucht“markiert.
3. Für diesen ersten Punkt im neuen Cluster werden die Punkte innerhalb seiner ε-Entfernung ebenfalls Teil desselben Clusters., Dieser Vorgang, bei dem alle Punkte in derselben Nachbarschaft zum selben Cluster gehören, wird dann für alle neuen Punkte wiederholt, die gerade der Clustergruppe hinzugefügt wurden.
4. Dieser Vorgang der Schritte 2 und 3 wird wiederholt, bis alle Punkte im Cluster ermittelt sind, d. h. alle Punkte innerhalb der ε-Nachbarschaft des Clusters wurden besucht und beschriftet.
5. Sobald wir mit dem aktuellen Cluster fertig sind, wird ein neuer nicht besuchter Punkt abgerufen und verarbeitet, was zur Entdeckung eines weiteren Clusters oder Rauschens führt. Dieser Vorgang wird wiederholt, bis alle Punkte als besucht markiert sind., Da am Ende alle Punkte besucht wurden, wurde jeder Punkt entweder als zu einem Cluster gehörend oder als Rausch markiert.

DBSCAN bietet einige große Vorteile gegenüber anderen Clustering-Algorithmen. Erstens ist überhaupt keine pe-festgelegte Anzahl von Clustern erforderlich. Es identifiziert auch Ausreißer als Geräusche, im Gegensatz zu Mean-Shift, die sie einfach in einen Cluster werfen, auch wenn der Datenpunkt sehr unterschiedlich ist. Darüber hinaus kann es beliebig große und beliebig geformte Cluster recht gut finden.,

Der Hauptnachteil von DBSCAN ist, dass es nicht so gut funktioniert wie andere, wenn die Cluster unterschiedlicher Dichte sind. Dies liegt daran, dass die Einstellung des Entfernungsschwellenwerts ε und der minPunkte zur Identifizierung der Nachbarschaftspunkte von Cluster zu Cluster variiert, wenn die Dichte variiert. Dieser Nachteil tritt auch bei sehr hochdimensionalen Daten auf, da wiederum die Abstandsschwelle ε schwer abzuschätzen ist.,

Erwartungsmaximierung (EM) Clustering mit Gaußschen Mischungsmodellen (GMM)

Einer der Hauptnachteile von K-Means ist die naive Verwendung des Mittelwerts für das Clusterzentrum. Wir können sehen, warum dies nicht der beste Weg ist, Dinge zu tun, indem wir uns das Bild unten ansehen. Auf der linken Seite sieht es für das menschliche Auge ziemlich offensichtlich aus, dass es zwei kreisförmige Cluster mit unterschiedlichem Radius gibt, die im gleichen Mittel zentriert sind. K-Means kann damit nicht umgehen, da die Mittelwerte der Cluster sehr nahe beieinander liegen., K-Means schlägt auch in Fällen fehl, in denen die Cluster nicht kreisförmig sind, wiederum als Ergebnis der Verwendung des Mittelwerts als Clusterzentrum.

Gaussian Mixture Models (GVM) geben uns mehr Flexibilität als K-Means. Bei GMMs gehen wir davon aus, dass die Datenpunkte gaußscharf verteilt sind; Dies ist eine weniger restriktive Annahme, als wenn man sagt, dass sie zirkulär sind, indem man den Mittelwert verwendet., Auf diese Weise haben wir zwei Parameter, um die Form der Cluster zu beschreiben: den Mittelwert und die Standardabweichung! Wenn wir ein Beispiel in zwei Dimensionen nehmen, bedeutet dies, dass die Cluster jede Art von elliptischer Form annehmen können (da wir eine Standardabweichung sowohl in x-als auch in y-Richtung haben). Somit ist jede Gaußsche Verteilung einem einzelnen Cluster zugeordnet.

Um die Parameter des Gaußschen für jeden Cluster zu ermitteln (z. B. Mittelwert und Standardabweichung), verwenden wir einen Optimierungsalgorithmus namens Expectation–Maximization (EM)., Schauen Sie sich die Grafik unten als Illustration der Gaußschen an, die an die Cluster angepasst sind. Dann können wir mit dem Prozess des Erwartungsmaximierungsclusterings mit GMMs fortfahren.

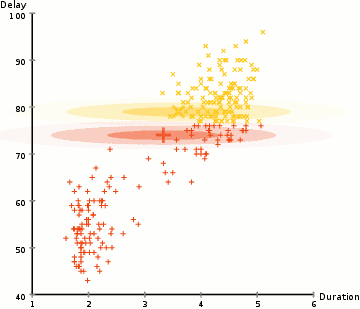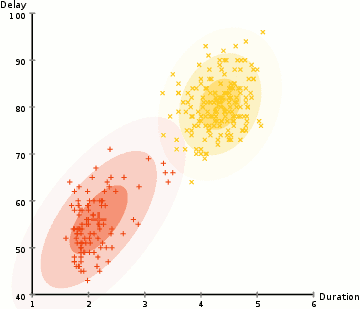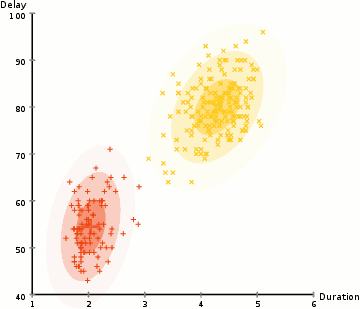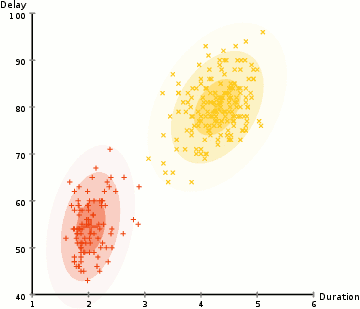
1. Wir beginnen, indem Sie die Anzahl der Cluster (wie K-Means hat) und zufällig initialisieren der GAUSS-Verteilung-Parameter für die einzelnen cluster., Man kann versuchen, ein gutes Guesstimate für die Anfangsparameter bereitzustellen, indem man sich auch die Daten anschaut. Beachten Sie jedoch, dass dies, wie in der obigen Grafik zu sehen ist, nicht zu 100% erforderlich ist, da die Gaußschen als sehr schlecht beginnen, aber schnell optimiert werden.
2. Berechnen Sie angesichts dieser Gaußschen Verteilungen für jeden Cluster die Wahrscheinlichkeit, dass jeder Datenpunkt zu einem bestimmten Cluster gehört. Je näher ein Punkt am Gaußschen Zentrum liegt, desto wahrscheinlicher gehört er zu diesem Cluster., Dies sollte intuitiv sinnvoll sein, da wir bei einer gaußschen Verteilung davon ausgehen, dass die meisten Daten näher am Zentrum des Clusters liegen.
3. Basierend auf diesen Wahrscheinlichkeiten berechnen wir einen neuen Satz von Parametern für die Gaußschen Verteilungen, sodass wir die Wahrscheinlichkeiten von Datenpunkten innerhalb der Cluster maximieren. Wir berechnen diese neuen Parameter unter Verwendung einer gewichteten Summe der Datenpunktpositionen, wobei die Gewichtungen die Wahrscheinlichkeiten des Datenpunkts sind, der zu diesem bestimmten Cluster gehört., Um dies visuell zu erklären, können wir uns die obige Grafik ansehen, insbesondere den gelben Cluster als Beispiel. Die Verteilung beginnt zufällig bei der ersten Iteration, aber wir können sehen, dass sich die meisten gelben Punkte rechts von dieser Verteilung befinden. Wenn wir eine Summe berechnen, die nach den Wahrscheinlichkeiten gewichtet ist, befinden sich die meisten Punkte rechts, obwohl sich einige Punkte in der Nähe des Zentrums befinden. Somit wird natürlich der Mittelwert der Verteilung näher an diese Menge von Punkten verschoben. Wir können auch sehen, dass die meisten Punkte „von oben rechts nach unten links“sind., Daher ändert sich die Standardabweichung, um eine Ellipse zu erstellen, die besser an diese Punkte angepasst ist, um die durch die Wahrscheinlichkeiten gewichtete Summe zu maximieren.
4. Die Schritte 2 und 3 werden iterativ bis zur Konvergenz wiederholt, wobei sich die Verteilungen von Iteration zu Iteration nicht wesentlich ändern.

Die Verwendung von GMMs bietet zwei wesentliche Vorteile. Erstens sind GMMs in Bezug auf die Clusterkovarianz viel flexibler als K-Mittelwerte; Aufgrund des Standardabweichungsparameters können die Cluster jede Ellipsenform annehmen, anstatt auf Kreise beschränkt zu sein., K-Means ist eigentlich ein Sonderfall von GMM, bei dem sich die Kovarianz jedes Clusters entlang aller Dimensionen 0 nähert. Zweitens, da GMMs Wahrscheinlichkeiten verwenden, können sie mehrere Cluster pro Datenpunkt haben. Wenn sich also ein Datenpunkt in der Mitte von zwei überlappenden Clustern befindet, können wir einfach seine Klasse definieren, indem wir sagen, dass er X-Prozent zu Klasse 1 und Y-Prozent zu Klasse 2 gehört. Dh GMMs unterstützen gemischte Mitgliedschaft.

Agglomeratives hierarchisches Clustering

Hierarchische Clustering-Algorithmen fallen in zwei Kategorien: Top-down oder Bottom-up., Bottom-up-Algorithmen behandeln jeden Datenpunkt zu Beginn als einen einzelnen Cluster und führen dann nacheinander Clusterpaare (oder Agglomeratpaare) zusammen, bis alle Cluster zu einem einzigen Cluster zusammengeführt wurden, der alle Datenpunkte enthält. Bottom-up hierarchisches Clustering wird daher hierarchisches agglomeratives Clustering oder HAC genannt. Diese Hierarchie von Clustern wird als Baum (oder Dendrogramm) dargestellt. Die Wurzel des Baumes ist der eindeutige Cluster, der alle Proben sammelt, wobei die Blätter die Cluster mit nur einer Probe sind., In der folgenden Grafik finden Sie eine Abbildung, bevor Sie zu den Algorithmusschritten übergehen

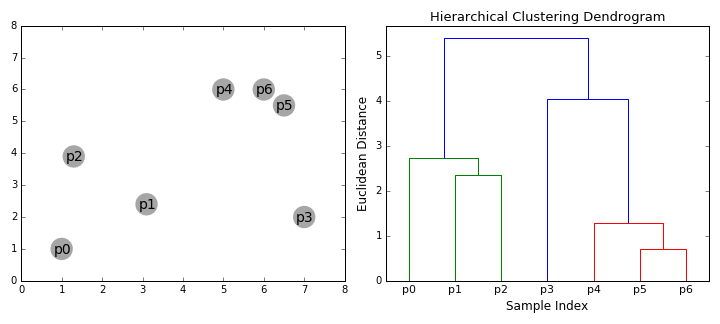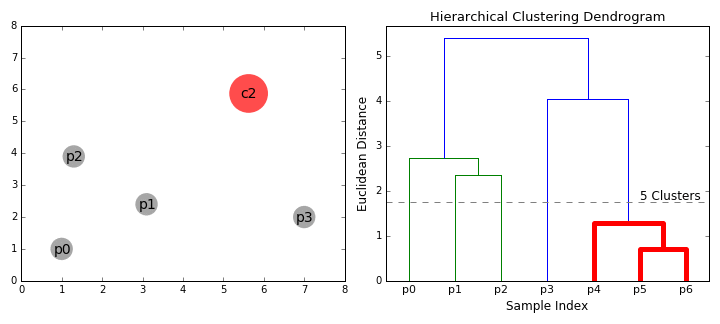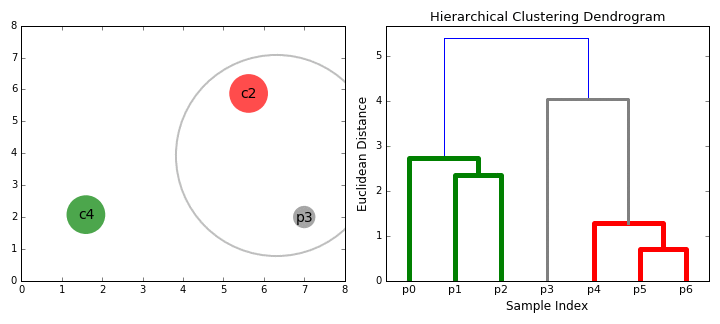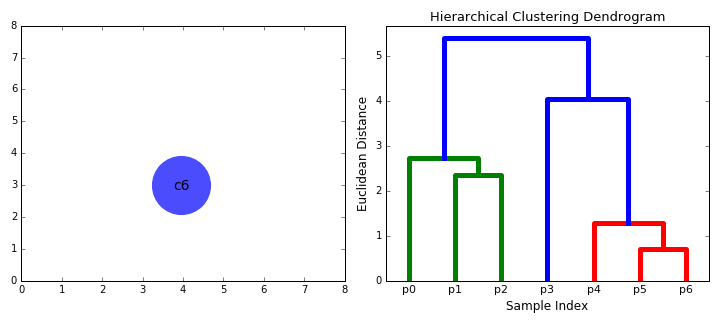
figcaption>

1. Wir beginnen damit, jeden Datenpunkt als einen einzelnen Cluster zu behandeln, dh wenn sich in unserem Datensatz X Datenpunkte befinden, haben wir X Cluster. Wir wählen dann eine Entfernungsmetrik aus, die den Abstand zwischen zwei Clustern misst., Als Beispiel verwenden wir die durchschnittliche Verknüpfung, die den Abstand zwischen zwei Clustern als durchschnittlichen Abstand zwischen Datenpunkten im ersten Cluster und Datenpunkten im zweiten Cluster definiert.
2. Bei jeder Iteration kombinieren wir zwei Cluster zu einem. Die beiden zu kombinierenden Cluster werden als solche mit der kleinsten durchschnittlichen Verknüpfung ausgewählt. Dh Gemäß unserer ausgewählten Entfernungsmetrik haben diese beiden Cluster den kleinsten Abstand zueinander und sind daher am ähnlichsten und sollten kombiniert werden.
3. Schritt 2 wird wiederholt, bis wir die Wurzel des Baumes i erreichen.,e Wir haben nur einen Cluster, der alle Datenpunkte enthält. Auf diese Weise können wir auswählen, wie viele Cluster wir am Ende haben möchten, indem wir einfach auswählen, wann die Cluster nicht mehr kombiniert werden sollen, dh wann wir aufhören, den Baum zu erstellen!

Hierarchisches Clustering erfordert nicht, dass wir die Anzahl der Cluster angeben, und wir können sogar auswählen, welche Anzahl von Clustern am besten aussieht, da wir einen Baum erstellen. Darüber hinaus reagiert der Algorithmus nicht empfindlich auf die Wahl der Entfernungsmetrik; Alle von ihnen funktionieren in der Regel gleich gut, während bei anderen Clustering-Algorithmen die Wahl der Entfernungsmetrik kritisch ist., Ein besonders guter Anwendungsfall hierarchischer Clustering-Methoden ist, wenn die zugrunde liegenden Daten eine hierarchische Struktur haben und Sie die Hierarchie wiederherstellen möchten; andere Clustering-Algorithmen können dies nicht tun. Diese Vorteile des hierarchischen Clusterings gehen zu Lasten geringerer Effizienz, da es im Gegensatz zur linearen Komplexität von K-Means und GMM eine Zeitkomplexität von O(n3) aufweist.