Verteilungen
Das Kernproblem im Herzen der Probleme mit dem Dirac Delta und ähnliche
mathematische Objekte ist das Problem der Differenzierbarkeit. Wie Dirac im obigen Zitat angegeben hat, geraten Sie nicht wirklich in Schwierigkeiten, wenn Sie seine δ-Funktion als symbolische Regel verwenden, wie sie auf andere Funktionen einwirkt; Er fährt jedoch fort, δ in seinen Berechnungen zu unterscheiden, und hier beginnen die Probleme wirklich., Wie kann man a priori wissen, „wann diese Operationen zulässig sind“, wenn man nicht einmal eine feste Definition der Objekte hat oder was es bedeuten würde, sie zu unterscheiden? Wir werden sehen, wie diese Fragen zur Ableitung neuer und streng definierter mathematischer Objekte führen.
Funktionale
Überlegen Sie, wie man normalerweise bestimmt die Ableitung (oder antiderivative) einer Funktion. Unter normalen Umständen haben Sie mit“ klassischen “ Funktionen eine genau definierte Regel, die beschreibt, wie eine Funktion einen Satz reeller Zahlen einem anderen Satz zuordnet, z. B. f : ℝ →ℝ., Angesichts dieser und der Definitionen des Integrals oder der Ableitung kann man dann eindeutig die Werte untersuchen, die diese Operatoren ergeben, wenn sie auf die Funktion angewendet werden. Im Falle von δ haben wir keine praktikable Definition, um in dieser Richtung vorzugehen. Stattdessen wird δ in der Praxis am deutlichsten dadurch definiert, wie es mit anderen, gut definierten Funktionen arbeitet (wie in (3)). Dies ist die Schlüsseleinsicht, die zur modernen Verteilungstheorie führt. Es stellt sich heraus, dass der richtige Weg, δ und eine große Klasse ähnlicher Objekte mathematisch zu behandeln, darin besteht, überhaupt nicht mehr zu versuchen, sie als Funktionen zu definieren., Diese Denkweise wird von Jean Dieudonne in seinem Rückblick auf (siehe) gut beschrieben:
… man beginnt mit einer Familie sehr „regulärer“ Funktionen (normalerweise mit
in Bezug auf differentielle Eigenschaften), die bestimmte (im Allgemeinen
integrale) Beziehungen erfüllen oder auf denen bestimmte Operationen möglich sind; und
dann entdeckt man, dass eine a priori größere Familie von Funktionen die gleichen Beziehungen erfüllt oder ähnlichen Operationen unterzogen werden kann. Viele
Fragen können dann natürlich gestellt werden: Ist diese neue Familie wirklich
anders als die erste?, Wenn ja, was sind die Beziehungen zwischen den
zwei Familien, und kann man eine genaue Beschreibung der neuen geben?
Erst in der letzten Phase der“ Vorgeschichte „wird ein revolutionärer Standpunkt entstehen, mit der Idee, dass
die“ neue Familie “ aus anderen Objekten als Funktionen bestehen könnte.
Die anderen angeführten Objekte sind funktionale. Sie können sich ein funktionales
als Funktion von Funktionen vorstellen., Da eine Funktion eine eindeutige Zuordnung von einem Satz von
– Zahlen zu einem anderen ist, kann ein funktionales F als Zuordnung F : C →ℝ,
wobei C eine Reihe von Funktionen ist. Das heißt, eine Funktion ordnet Funktionen realen
– Zahlen zu., Ein einfaches Beispiel für eine Funktion dieses Typs ist das definitive Integral:

dies nimmt eindeutig eine Funktion f aus einer Reihe von entsprechend integrierbaren Funktionen und ordnet sie einer reellen Zahl, dem Wert des Integrals oder der Fläche unter der Kurve f(x) zwischen a und b zu. , Man kann sich eine unendliche Anzahl von Funktionalen und Mengen von Funktionalen vorstellen; Man könnte sogar weiterhin Zuordnungen von Mengen von Funktionalen zu reellen Zahlen verallgemeinern und definieren. Das ist weder hier noch da. Wichtig ist, dass mit dem Funktionskonzept Verteilungen definiert werden können.
Der Satz von Testfunktionen
Wir benötigen eine weitere Definition, um unser Ziel zu erreichen. Dies entspricht der Angabe der Menge C von Funktionen, aus denen die Verteilungen Funktionen reellen Zahlen zuordnen., Funktionen werden häufig in Mengen gesammelt, die ihren Grad an Kontinuität, Differenzierbarkeit und die Kontinuität ihrer Ableitungen angeben. Wir sagen, eine Funktion f befindet sich in der Menge c⁰ (schreiben Sie f ∈ c⁰), wenn sie über die gesamte reelle Linie in dem Sinne kontinuierlich ist, dass die Grenze an allen Punkten gleich ist, wenn sie von links oder rechts genommen wird.es ist nicht unbedingt unterscheidbar. Wir sagen, dass f ∈ C1, wenn seine Ableitung existiert und kontinuierlich ist, dh f ‚ ∈ c⁰. Zum Beispiel ist die Funktion g(x) = |x| kontinuierlich, aber nicht differenzierbar bei x= 0; g ist in c⁰, aber nicht in C1., Wir können dies verallgemeinern und sagen, dass cⁿ die Menge von Funktionen ist, die für kontinuierliche Funktionen ihre ersten n Ableitungen haben, wobei n eine ganze Zahl ist.
Wenn n größer wird, werden die Mengen gewissermaßen „kleiner“; Sie können immer Funktionen finden (unendlich viele!), die in Cⁿ sind, aber nicht cⁿ ⁺ 1. Diese „Kontinuitätsräume“ bilden daher eine Folge verschachtelter Teilmengen, wie unten dargestellt.

Am Ende dieser unendlichen Abfolge von Funktionsmengen finden wir die Menge
das ist natürlich die Menge aller Funktionen, die unendlich viele kontinuierliche Ableitungen haben. Viele bekannte und freundliche Funktionen sind in dieser Klasse (z.B. sin(x); cos(x); eˣ; alle Polynome)., Diese Funktionen werden als „glatt“ oder „gut erzogen“ bezeichnet, da man die Differenzierung so oft durchführen kann, wie man ohne Sorgfalt möchte. Aber während dieses Set sicherlich unendlich viele Mitglieder hat, sind sie selten in dem Sinne, dass die meisten Funktionen nicht so gut erzogen sind.
Die Menge, die für die Definition von Verteilungen geeignet ist, ist noch kleiner
als diese. Es erfordert ein zusätzliches Kriterium: dass die Funktionen kompakte Unterstützung haben. Dieser Fachbegriff bedeutet einfach, dass eine Funktion innerhalb einer endlichen Domäne Werte ungleich Null hat und außerhalb dieser einheitlich Null ist., Wir verwenden daher die Notation
, um die Menge der unendlich kontinuierlich differenzierbaren Funktionen mit kompakter Unterstützung zu bezeichnen, und rufen funktionen Testfunktionen. Um eine Klasse von Funktionalen zu definieren, die diesen Satz als Domäne verwenden, sollten wir sicher sein, dass tatsächlich Mitglieder dieses Satzes vorhanden sind., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Die Definition
Ab diesem Zeitpunkt ist die Definition einer Verteilung unkompliziert. Eine Verteilung ist eine lineare Funktion
Das heißt, es ist eine Zuordnung von der Menge der Testfunktionen zu einer reellen Zahl. Analog dazu, wie eine bestimmte Funktion auf eine Eingangsnummer einwirkt und eine Ausgabe erzeugt, werden spezifische Verteilungen dadurch definiert, wie sie Testfunktionen in Zahlen umwandeln., Die Verteilungsfunktion der Testfunktion φ kann als T (φ) oder allgemein als〈T, φ〉 geschrieben werden.
Man kann jetzt sehen, warum Verteilungen generalisierte Funktionen genannt werden. Für alle
klassische Funktion, für die das integral

gut definiert ist, ist eine entsprechende Verteilung F so, dass 〈F,φ〉gibt den Wert dieser Integrale., Es gibt jedoch auch Verteilungen, die nicht mit klassischen Funktionen übereinstimmen; Verteilungen sind allgemeiner. Wie jetzt klar sein sollte, ist das kanonische Beispiel einer Verteilung, die keiner klassischen Funktion entspricht, das Dirac δ., Wir kommen daher endlich zu einer vollständig strengen Definition von δ als Verteilung, so dass
Die verallgemeinerte oder „schwache“ Ableitung
Die δ-Verteilung ist nur eine von unendlich vielen Verteilungen, die nicht
klassischen Funktionen entsprechen. Wir können einige mehr davon erhalten, indem wir δ im Sinne von Verteilungen unterscheiden., Aber wie löst das Konzept einer
– Verteilung das zuvor diskutierte Differenzierungsproblem? Wir müssen nur das Konzept der Differenzierung verallgemeinern, um es auf Verteilungen anzuwenden.
Betrachten Sie eine Funktion f ∈ C1, so dass sie kontinuierlich differenzierbar ist. Wenn wir die Integration nach Teilen berechnen, sehen wir, dass

Der Begriff in den Klammern verschwindet seit φ, als Testfunktion, hat kompakte Unterstützung., Dies verallgemeinert zu einer Verteilung, sagen wir F‘, entsprechend der Funktion f‘:

Diese Berechnung verallgemeinert sich ganz leicht auf Verteilungen, die nicht einer klassischen Funktion f entsprechen., Auf diese Weise können wir die Ableitung T‘ von T im Sinne von Verteilungen definieren:

Dies wird manchmal auch als schwache Ableitung bezeichnet, da sie Ableitungen auf Funktionen ausdehnt, die normalerweise nicht unterscheidbar wären. Dies verallgemeinert sich noch weiter auf Derivate höherer Ordnung., Wir können die n-te Ableitung einer Verteilung T als T ⁽ ⁿ ⁾ definieren, wobei letztere die Verteilung ist, so dass

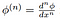
ist die klassische Ableitung der Testfunktion, die
Dadurch wird der Kampf, mit dem Dirac und andere bei der Differenzierung der δ-Funktion konfrontiert waren, vollständig beseitigt. Nach dem, was wir hier definiert haben, durchsucht eine Ableitung von δ einfach den Wert einer anderen Funktionsableitung bei Null., Formal

Dies stellt einen strengen mathematischen Rahmen für die Ableitungen von δ, erschien in der Literatur, lange bevor diese Theorie zustande kam.
Es gibt eine Reihe anderer Operationen, die für Funktionen gelten, die verallgemeinert wurden, um sie auf Verteilungen anzuwenden. Sie können mit Laplace-und Fourier-Transformationen addiert und subtrahiert, gewunden und transformiert werden., Es ist jedoch unmöglich, die Multiplikation von Verteilungen so zu definieren, dass die Algebra erhalten bleibt, die für klassische Funktionen gilt (der Schwartz-Unmöglichkeitssatz).