Es gibt eine alte Ansicht, die immer noch weit verbreitet ist, dass das, was den Menschen besonders macht-was uns von den „Bestien des Feldes“ unterscheidet-ist, dass wir rational sind. Woraus besteht Rationalität? Das ist eine ärgerliche Frage, aber eine mögliche Antwort geht ungefähr so: Wir manifestieren unsere Rationalität, indem wir uns an Aktivitäten beteiligen, bei denen Behauptungen aufgestellt und mit Gründen untermauert werden, Handeln im Einklang mit Gründen und Überzeugungen, Rückschlüsse aus verfügbaren Beweisen ziehen, und so weiter.,
Diese Argumentationsaktivität kann gut und schlecht durchgeführt werden.es kann richtig oder falsch gemacht werden. Logik ist die Disziplin, die darauf abzielt, gutes Denken von Schlechtem zu unterscheiden.
Gutes Denken ist nicht unbedingt effektives Denken. Wie wir in einem nachfolgenden Kapitel über logische Irrtümer sehen werden, ist schlechtes Denken allgegenwärtig und oft äußerst effektiv—in dem Sinne, dass die Menschen oft davon überzeugt werden. In der Logik ist der Standard der Güte nicht Wirksamkeit im Sinne von Überzeugungskraft, sondern Korrektheit nach logischen Regeln.,
betrachten Sie Zum Beispiel Hitler. Er überredete eine ganze Nation, eine Vielzahl von Vorschlägen zu unterbreiten, die nicht nur falsch, sondern auch geradezu böse waren. Sie werden nicht überrascht sein zu hören, dass, wenn Sie es kritisch untersuchen, seine Argumentation nicht logisch Muster passieren. Hitlers Argumente waren wirksam, aber nicht logisch korrekt. Darüber hinaus gehen seine überzeugenden Techniken über die Argumentation im Sinne der Sicherung von Ansprüchen mit Gründen hinaus. Hitler verließ sich auf Drohungen, emotionale Manipulation, nicht unterstützte Behauptungen usw. Es gibt viele rhetorische Tricks, mit denen man überzeugen kann.,
In der Logik studieren wir die Regeln und Techniken, die es uns ermöglichen, gutes, korrektes Denken von schlechtem, falschem Denken zu unterscheiden.
Da es eine Vielzahl verschiedener Arten von Überlegungen und Methoden gibt, mit denen jeder dieser Typen bewertet werden kann, sowie verschiedene unterschiedliche Ansichten darüber, was korrektes Denken ausmacht, gibt es viele Ansätze für das logische Unternehmen. Wir sprechen von Logik, aber auch von Logik. Eine Logik ist nur eine Reihe von Regeln und Techniken, um gutes von Schlechtem zu unterscheiden., Eine Logik muss präzise Standards für die Bewertung von Argumenten formulieren und Methoden zur Anwendung dieser Standards auf bestimmte Instanzen entwickeln.
Grundbegriffe
Argumentation beinhaltet Ansprüche oder Aussagen—sie zu machen und sie mit Gründen zu untermauern, ihre Konsequenzen zu ziehen. Sätze sind die Dinge, die wir behaupten, behaupten, behaupten.
Sätze sind die Arten von Dingen, die wahr oder falsch sein können. Sie werden durch deklarative Sätze ausgedrückt., Wir verwenden solche Sätze, um alle möglichen Behauptungen zu machen, von routinemäßigen Tatsachen („die Erde dreht sich um die Sonne“) über große metaphysische Thesen („Die Realität ist ein unveränderliches, eigenschaftsloses, einheitliches Absolutes“) bis hin zu Behauptungen über Moral („es ist falsch, Fleisch zu essen“).
Es ist wichtig, Sätze in der deklarativen Stimmung, die Sätze ausdrücken, von Sätzen in anderen Stimmungen zu unterscheiden, die dies nicht tun. Fragesätze stellen zum Beispiel Fragen („Regnet es?“), und imperative Sätze geben Befehle aus („Kein Kerosin trinken.”)., Es macht keinen Sinn zu fragen, ob diese Art von Sätzen Wahrheiten oder Unwahrheiten ausdrücken, also drücken sie keine Sätze aus.
Wir unterscheiden auch Sätze von den Sätzen, die sie ausdrücken, weil ein einzelner Satz durch verschiedene Sätze ausgedrückt werden kann. „It‘ s raining“ und „es regnet“ drücken beide den Satz aus, dass es regnet; ein Satz macht es auf Englisch, der andere auf Deutsch. Auch“ John loves Mary „und“ Mary is loved by John “ drücken beide den gleichen Satz aus.
Die grundlegende Einheit des Denkens ist das Argument., In der Logik meinen wir mit“ Argument“keine Meinungsverschiedenheit, keine schreiende Übereinstimmung; vielmehr definieren wir den Begriff genau:
Argument = eine Reihe von Sätzen, von denen einer, die Schlussfolgerung, von den anderen, den Prämissen, unterstützt wird (werden soll).
Wenn wir argumentieren, indem wir Ansprüche stellen und sie mit Gründen sichern, dann ist die Behauptung, die gesichert wird, die Schlussfolgerung eines Arguments; Die Gründe, die gegeben werden, um es zu unterstützen, sind die Prämissen des Arguments., Wenn wir argumentieren, indem wir eine Inferenz aus einer Reihe von Anweisungen ziehen, dann ist die Inferenz, die wir zeichnen, die Schlussfolgerung eines Arguments, und die Aussagen, aus denen es gezogen wird, sind die Prämissen.
Wir fügen die übergeordnete Absicherung- „soll sein“ – in die Definition ein, um Platz für schlechte Argumente zu schaffen. Ein schlechtes Argument, sehr grob gesagt, ist eines, bei dem die Prämissen die Schlussfolgerung nicht unterstützen; Die Prämissen eines guten Arguments unterstützen die Schlussfolgerung tatsächlich.
Analyse der Argumente
Die folgende Passage drückt ein Argument aus:
So auch diese passage:
Auch hier besteht der ultimative Zweck der Logik darin, Argumente zu bewerten—um das Gute vom Schlechten zu unterscheiden. Dazu sind Unterscheidungen, Definitionen, Prinzipien und Techniken erforderlich, die in den folgenden Kapiteln beschrieben werden. Im Moment konzentrieren wir uns darauf, Argumente zu identifizieren und zu rekonstruieren.
Die erste Aufgabe besteht darin, Argumente zu erläutern-ihre Prämissen und Schlussfolgerungen explizit anzugeben., Eine sinnvolle Möglichkeit, dies zu tun, besteht darin, einfach deklarative Sätze aufzulisten, die die relevanten Vorschläge ausdrücken, wobei eine Linie die Räumlichkeiten von der Schlussfolgerung trennt:
- McDonald ‚ s zahlt seinen Arbeitern sehr niedrige Löhne.
- Die Tiere, die McDonald ‚ s-Fleisch liefern, werden unter beklagenswerten Bedingungen aufgezogen.
- McDonald ‚ s Essen ist sehr ungesund.
- / \daher sollten Sie nicht bei McDonald ‚ s essen.
Dies ist eine Erläuterung der ersten argumentativen Passage oben., Um die Schlussfolgerung eines Arguments zu identifizieren, ist es hilfreich, sich selbst zu fragen: „Was versucht diese Person, mich zu überzeugen, zu glauben, indem sie diese Dinge sagt? Was ist der ultimative Punkt dieser Passage?“Die Antwort ist in diesem Fall ziemlich klar. Ein weiterer Hinweis darauf, was in der Passage vor sich geht, liefert das Wort „weil“ im dritten Satz. Zusammen mit anderen Wörtern wie „seit“ und „für“ zeigt es das Vorhandensein einer Prämisse an. Wir können solche Wörter Prämissenmarker nennen. Das Symbol “ / ∴ „kann als Abkürzung für „daher“ gelesen werden.,“Zusammen mit Ausdrücken wie „folglich“, „so“, „daraus folgt“ und „was das impliziert“, „daher“ ist ein Indikator dafür, dass die Schlussfolgerung des Arguments folgen wird. Wir nennen solche Locutions als Marker. Ein solcher Marker ist im ersten Argument nicht vorhanden, aber wir sehen einen im zweiten, der so erklärt werden kann:
- Das Universum ist riesig und komplex.
- Das Universum zeigt einen erstaunlichen Grad an Ordnung.
- Die Planeten umkreisen die Sonne nach regulären Gesetzen.
- Die kleinsten Teile der Tiere sind genau so angeordnet, dass sie ihren Zwecken dienen.,
- Eine solche Reihenfolge und Komplexität kann nicht zufällig auftreten.
- / \deshalb muss das Universum das Produkt eines Designers von enormer Kraft und Intellekt sein: Gott.
Einige Vergleichspunkte zu unserer ersten Erklärung sind hier erwähnenswert. Zunächst wurden wir, wie bereits erwähnt, durch das Wort „daher“ auf die Schlussfolgerung aufmerksam gemacht.“Zweitens erforderte diese Passage viel mehr Umschreibung als die erste. Der zweite Satz ist fragend, nicht deklarativ und drückt daher keinen Satz aus., Da Argumente per Definition Sammlungen von Sätzen sind, müssen wir uns bei der Erklärung auf deklarative Sätze beschränken. Da die Antwort auf die rhetorische Frage des zweiten Satzes eindeutig „Ja“ lautet, paraphrasieren wir wie gezeigt. Der dritte Satz drückt zwei Sätze aus, also trennen wir sie in unserer Erklärung; Jeder ist eine Prämisse.
Wenn wir also ein Argument explizieren, müssen wir manchmal nehmen, was in der argumentativen Passage vorhanden ist, und es leicht ändern, so dass alle Sätze, die wir aufschreiben, die im Argument vorhandenen Sätze ausdrücken., Das ist Paraphrasierung. Zu anderen Zeiten müssen wir noch mehr tun. Zum Beispiel müssen wir möglicherweise Sätze einführen, die in der argumentativen Passage nicht explizit erwähnt werden, aber zweifellos in der Argumentation des Arguments verwendet werden.
Es gibt ein griechisches Wort für argumentative Passagen, die bestimmte Sätze unaufgefordert lassen: Enthymeme. Hier ist ein Beispiel:
Hier lauert eine implizite Prämisse im Hintergrund—etwas, das nicht gesagt wurde, das aber wahr sein muss, damit das Argument durchgeht. Wir brauchen eine Behauptung, die die Prämisse mit der Schlussfolgerung verbindet—die die Lücke zwischen ihnen schließt. So etwas wie dieses: Ein allliebender Gott würde nicht zulassen, dass unschuldige Menschen leiden. Oder vielleicht: Weit verbreitetes Leiden ist unvereinbar mit der Idee einer allliebenden Gottheit. Die Prämisse weist auf Leiden hin, während die Schlussfolgerung über Gott liegt; Diese Sätze verbinden diese beiden Behauptungen., Eine vollständige Erklärung der argumentativen Passage würde einen Satz wie diesen deutlich machen:
- Viele unschuldige Menschen auf der ganzen Welt leiden.
- Ein allliebender Gott würde nicht zulassen, dass unschuldige Menschen leiden.
- / \daher kann es keinen allliebenden Gott geben.
Dies ist das Kennzeichen der Arten von stillschweigenden Prämissen, die wir aufdecken wollen: Wenn sie falsch sind, untergraben sie das Argument., Oft sind solche Prämissen aus einem bestimmten Grund nicht validiert: Es handelt sich um kontroverse Behauptungen, die Beweise erfordern, um sie zu unterstützen; Der Argumenter lässt sie also aus und zieht es vor, nicht festzustecken. Wenn wir sie jedoch herausziehen, können wir einen robusteren dialektischen Austausch erzwingen und das Argument auf den Kern der Sache konzentrieren. In diesem Fall wäre eine Diskussion über die Vereinbarkeit von Gottes Güte und Bösem in der Welt in Ordnung. Zu diesem Thema gibt es viel zu sagen., Philosophen und Theologen haben im Laufe der Jahrhunderte ausgeklügelte Argumente entwickelt, um die Idee zu verteidigen, dass Gottes Güte und menschliches Leiden tatsächlich vereinbar sind.
Bisher war unsere Argumentationsanalyse nicht besonders tief. Wir haben festgestellt, wie wichtig es ist, die Schlussfolgerung zu identifizieren und die Prämissen klar zu formulieren, aber wir haben nicht untersucht, auf welche Weise Prämissen ihre Schlussfolgerungen stützen können. Wir haben lediglich festgestellt, dass Räumlichkeiten gemeinsam Schlussfolgerungen unterstützen., Wir haben uns nicht angesehen, wie sie das tun, welche Art von Beziehungen sie zueinander haben. Dies erfordert eine tiefere Analyse.
Oft unterstützen verschiedene Prämissen eine Schlussfolgerung—oder eine andere Prämisse—einzeln, ohne Hilfe anderer. Betrachten Sie dieses einfache Argument:
Die Sätze 1 und 2 unterstützen die Schlussfolgerung, Satz 3—und zwar unabhängig voneinander. Jeder gibt uns einen Grund zu glauben, dass der Krieg ungerecht war, und jeder steht als Grund, auch wenn wir annehmen, dass der andere nicht wahr war; Dies ist das Zeichen unabhängiger Prämissen.
Es kann hilfreich sein, insbesondere wenn Argumente komplexer sind, Diagramme zu zeichnen, die die Beziehungen zwischen Prämissen und Schlussfolgerungen darstellen., Wir könnten das obige Argument wie folgt darstellen:
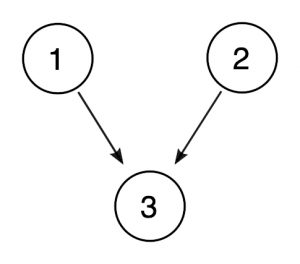
In einem solchen Diagramm stellen die eingekreisten Zahlen die Sätze dar und die Pfeile stellen das Verhältnis der Unterstützung von einem Satz zu einem anderen dar. Da die Sätze 1 und 2 jeweils 3 unabhängig voneinander unterstützen, erhalten sie ihre eigenen Pfeile.
Andere Beziehungen zwischen Räumlichkeiten sind möglich. Manchmal unterstützen Prämissen Schlussfolgerungen nur indirekt, indem sie uns einen Grund geben, einer anderen Prämisse zu glauben, die zwischen den beiden Behauptungen liegt., Betrachten Sie das folgende Argument:
In diesem Beispiel bietet Satz 1 Unterstützung für Satz 2 (das Wort „daher“ ist ein Hinweis), während Satz 2 die Schlussfolgerung in 3 direkt unterstützt., Wir würden die Beziehungen zwischen diesen Sätzen so darstellen:

Manchmal müssen Prämissen zusammenarbeiten, um einen anderen Anspruch zu unterstützen, nicht weil einer von ihnen Grund zum Glauben an den anderen bietet, sondern weil keiner von beiden die Unterstützung bietet, die für sich allein benötigt wird; Wir nennen solche Sätze gemeinsame Prämissen. Betrachten Sie Folgendes:
In diesem Argument unterstützen weder Prämisse 1 noch Prämisse 2 die Schlussfolgerung für sich; Vielmehr liefert die zweite Prämisse sozusagen einen Schlüssel, der die Schlussfolgerung aus der bedingten Prämisse 1 freigibt. Wir können eine solche Interdependenz diagrammatisch mit Klammern angeben, also:
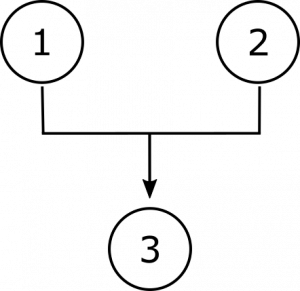
Diagrammargumente auf diese Weise können sowohl hilfreich sein, um zu verstehen, wie sie funktionieren, als auch um jeden Versuch zu informieren, sich kritisch mit ihnen zu beschäftigen., Man kann im ersten Argument deutlich erkennen, dass jegliche Überlegungen, die einem der unabhängigen Räumlichkeiten zuwiderlaufen, die Unterstützung für die Schlussfolgerung nicht vollständig untergraben werden, da es noch eine andere Prämisse gibt, die ihr ein gewisses Maß an Unterstützung bietet. Im zweiten Argument würden jedoch Gründe, die gegen die zweite Prämisse sprechen, die Unterstützung für die Schlussfolgerung an ihrer Wurzel abschneiden; und alles, was der ersten Prämisse widerspricht, wird die zweite unterstützen müssen. Und im dritten Argument werden Überlegungen, die einem der gemeinsamen Räumlichkeiten widersprechen, die Unterstützung für die Schlussfolgerung untergraben., Besonders wenn Argumente komplexer sind, können solche visuellen Hilfsmittel uns helfen, alle im Argument enthaltenen Schlussfolgerungen zu erkennen.
Vielleicht wird es nützlich sein, mit einem etwas komplexeren Argument zu schließen. Betrachten wir die Natur der Zahlen:
Die Schlussfolgerung dieses Arguments ist der letzte Satz, dass Zahlen abstrakte Objekte sind. Beachten Sie, dass die erste Prämisse uns die Wahl zwischen diesem Anspruch und einer Alternative gibt—dass sie konkret sind. Die zweite Prämisse bestreitet diese Alternative, und so arbeiten die Prämissen 1 und 2 zusammen, um die Schlussfolgerung zu stützen:
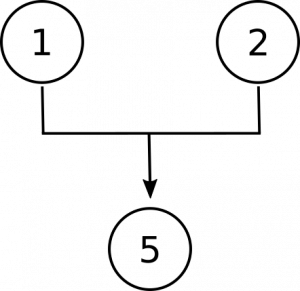
Jetzt müssen wir in unserem Diagramm Platz für die Sätze 3 und 4 schaffen. Sie sind da, um uns Gründe für die Annahme zu geben, dass Zahlen keine konkreten Objekte sind., Erstens durch die Behauptung, dass Zahlen sich nicht wie konkrete Objekte im Raum befinden, und zweitens durch die Behauptung, dass Zahlen nicht wie konkrete Objekte mit anderen Objekten interagieren. Dies sind separate, unabhängige Gründe für die Annahme, dass sie nicht konkret sind, daher erhalten wir dieses Diagramm:
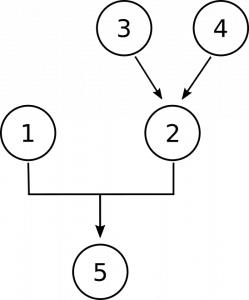
Logik und Philosophie
Im Mittelpunkt des logischen Unternehmens steht eine philosophische Frage: Was macht ein gutes Argument aus? Das heißt, was ist es für einen Anspruchssatz, um einen anderen Anspruch zu unterstützen? Oder vielleicht: Wann sind wir berechtigt, Schlussfolgerungen zu ziehen?, Um diese Fragen zu beantworten, haben Logiker eine Vielzahl von logischen Systemen entwickelt, die verschiedene Arten von Argumenten abdecken und verschiedene Prinzipien und Techniken anwenden. Viele der in der Logik entwickelten Werkzeuge können über die Grenzen der Philosophie hinaus angewendet werden. Der Mathematiker, der einen Satz beweist, der Informatiker, der einen Computer programmiert, der Linguist, der die Struktur der Sprache modelliert—all dies verwendet logische Methoden., Da Logik eine so breite Anwendung hat und aufgrund der formalen/mathematischen Raffinesse vieler logischer Systeme einen einzigartigen Platz im philosophischen Lehrplan einnimmt. Eine Klasse in Logik unterscheidet sich typischerweise von anderen Philosophieklassen dadurch, dass sehr wenig Zeit damit verbracht wird, sich direkt mit den „großen Fragen“ zu beschäftigen und diese zu beantworten.eher, Man kommt sehr schnell zur Sache, logische Formalismen zu lernen. Die Fragen, die Logik zu beantworten versucht, sind wichtige philosophische Fragen, aber die Techniken, die entwickelt wurden, um sie zu beantworten, sind es wert, selbst studiert zu werden.,
Das bedeutet aber nicht, dass wir Logik und Philosophie nur als tangential verwandt betrachten sollten, im Gegenteil, sie sind tief verwoben. Für alle formalen Schnickschnack, die im neuesten High-End-logischen System enthalten sind, ist es im Grunde Teil der Bemühungen, die grundlegende Frage zu beantworten, was daraus folgt. Darüber hinaus ist Logik für den praktizierenden Philosophen auf mindestens drei andere Arten nützlich.
Philosophen versuchen, tiefe, ärgerliche Fragen zu beantworten—über die Natur der Realität, was ein gutes Leben ausmacht, wie man eine gerechte Gesellschaft schafft und so weiter., Sie geben ihre Antworten auf diese Fragen, und sie unterstützen diese Antworten mit Gründen. Dann betrachten andere Philosophen ihre Argumente und antworten mit Ausarbeitungen und Kritikpunkten—eigenen Argumenten. Die Philosophie wird geführt und macht Fortschritte durch den Austausch von Argumenten. Da sie das Hauptinstrument ihres Handels sind, wissen Philosophen besser etwas darüber, was gute Argumente ausmacht! Logik ist daher für die Praxis der Philosophie unerlässlich.,
Aber Logik ist nicht nur ein Werkzeug zur Bewertung philosophischer Argumente; es hat den Verlauf der laufenden philosophischen Konversation verändert. Da Logiker formale Systeme entwickelten, um die Struktur eines immer breiteren Spektrums diskursiver Praktiken zu modellieren, konnten Philosophen ihre Erkenntnisse direkt auf traditionelle philosophische Probleme anwenden und zuvor verborgene Untersuchungswege erkennen. Jahrhunderts hat die Verbreitung neuartiger Ansätze in der Logik eine Revolution in der Praxis der Philosophie ausgelöst., Jahrhunderts einen kontinuierlichen Versuch darstellte, sich mit neuen Entwicklungen in der Logik und dem philosophischen Fokus auf die Sprache auseinanderzusetzen, den sie zu fordern schienen. Kein philosophisches Thema—von der Metaphysik über Ethik bis hin zur Erkenntnistheorie und darüber hinaus-blieb von dieser Revolution unberührt.
Schließlich ist die Logik selbst die Quelle faszinierender philosophischer Fragen. Die grundlegende Frage in seinem Herzen—was ist es für einen Anspruch, von anderen zu folgen?,- verzweigt sich in unzählige Richtungen und bietet fruchtbaren Boden für philosophische Spekulationen. Es gibt Logik, und dann gibt es Philosophie der Logik. Logik wird zum Beispiel als „formal“ bezeichnet. Was bedeutet das? Es ist eine überraschend schwierige Frage zu beantworten. Unsere einfachsten logischen Formulierungen von Bedingungssätzen (die „wenn“ beinhalten) führen zu offensichtlichen Paradoxien. Wie sollen diese gelöst werden? Sollten unsere Formalismen geändert werden, um die natursprachlichen Bedeutungen von Bedingungen besser einzufangen? Was ist die richtige Beziehung zwischen logischen Systemen und natürlichen Sprachen?,
Traditionell haben die meisten Logiker akzeptiert, dass Logik „bivalent“ sein sollte: Jeder Satz ist entweder wahr oder falsch. Natürliche Sprachen enthalten jedoch vage Begriffe, deren Grenzen der Anwendbarkeit nicht immer klar sind. Zum Beispiel „Glatze“: Für bestimmte Themen könnten wir geneigt sein zu sagen, dass sie auf dem besten Weg zur Vollkahlheit sind, aber noch nicht ganz da; Auf der anderen Seite würden wir nur ungern sagen, dass sie nicht kahl sind. Es gibt Zwischenfälle. Für solche Fälle möchten wir zum Beispiel sagen, dass der Satz, dass Fredo kahl ist, weder wahr noch falsch ist., Einige Logiker haben Logiken entwickelt, die nicht bivalent sind, um mit dieser Art von Sprachphänomen umzugehen. Einige fügen einen dritten Wahrheitswert hinzu: „weder “ noch“ unbestimmt “ zum Beispiel. Andere führen unendliche Grade der Wahrheit ein (dies wird „Fuzzy Logic“genannt). Diese Logiken weichen von traditionellen Ansätzen ab. Sind sie daher in gewissem Sinne falsch? Oder haben sie Recht und die Traditionalisten falsch? Oder stellen wir überhaupt eine vernünftige Frage, wenn wir fragen, ob ein bestimmtes logisches System richtig oder falsch ist?, Können wir sogenannte logische „Pluralisten“ sein, die eine Vielzahl inkompatibler Logiken akzeptieren, zum Beispiel davon, ob sie nützlich sind?
Diese Art von Fragen gehen natürlich über den Rahmen dieses Einleitungstextes hinaus. Sie sind enthalten, um Ihnen ein Gefühl dafür zu geben, wie weit man das Studium der Logik gehen kann. Die Aufgabe für jetzt ist es jedoch, diese Studie zu beginnen.
Erläutern Sie zunächst die folgenden Argumente, paraphrasieren Sie sie nach Bedarf und schließen Sie stillschweigende Prämissen nur ein, wenn Sie dies ausdrücklich angewiesen haben. Zeichnen Sie als nächstes die Argumente.,
- Zahlen müssen, wenn sie überhaupt existieren, entweder konkrete oder abstrakte Objekte sein. Konkrete Objekte–wie Planeten und Menschen-können in Ursache-Wirkungs-Beziehungen mit anderen Dingen interagieren. Zahlen fehlen diese Fähigkeit. Daher sind Zahlen abstrakte Objekte.
- Todesstrafe abschaffen! Warum? Es ist unmoralisch. Zahlreiche Studien haben gezeigt, dass es rassische Voreingenommenheit in seiner Anwendung gibt. Der Anstieg der DNA-Tests hat Dutzende von Insassen in der Todeszelle entlastet; Wer weiß, wie viele unschuldige Menschen in der Vergangenheit getötet wurden? Die Todesstrafe ist auch unpraktisch., Rache ist kontraproduktiv: „Ein Auge für ein Auge lässt die ganze Welt blind“, wie Gandhi sagte. Darüber hinaus sind die Kosten für die Anfechtung von Todesstrafsachen mit ihren endlosen Berufungen enorm.
- Ein gerechtes Wirtschaftssystem würde eine gerechte Verteilung der Ressourcen und eine Ausbeutung ohne Ausbeutung beinhalten. Der Kapitalismus ist ein ungerechtes Wirtschaftssystem. Unter dem Kapitalismus ist die typische Verteilung des Reichtums zugunsten der Reichen stark verzerrt., Und Arbeiter werden ausgebeutet: Trotz ihrer wesentlichen Rolle bei der Herstellung von Waren für den Markt gehen die meisten Gewinne aus dem Verkauf dieser Waren an die Eigentümer von Unternehmen, nicht an ihre Arbeiter.
- Geist und Gehirn sind nicht identisch. Wie können Dinge identisch sein, wenn sie unterschiedliche Eigenschaften haben? Es gibt eine Eigenschaft, die Geist und Gehirn nicht teilen: Das Gehirn ist teilbar, der Geist jedoch nicht. Wie alle materiellen Dinge kann das Gehirn in Teile unterteilt werden-verschiedene Hälften, Regionen, Neuronen usw. Aber der Geist ist eine Einheit. Es ist meine Denkessenz, in der ich keine getrennten Teile erkennen kann.,
- Jeder arbeitsfähige Erwachsene sollte an der Belegschaft teilnehmen. Je mehr Menschen arbeiten, desto größer ist der Reichtum der Nation, von dem alle wirtschaftlich profitieren. Darüber hinaus gibt es keinen Ersatz für die Würde, die Arbeitnehmer bei der Arbeit finden. Die Regierung sollte daher Steuergutschriften ausgeben, um Menschen zum Einstieg in die Belegschaft zu ermutigen.
- Die Symbole vor der Schlussfolgerung“ / \daher “ repräsentieren das Wort „daher.“Das ist nicht immer der Grund., Einige Behauptungen bleiben stillschweigend, nur weil jeder sie akzeptiert und sie explizit anzugeben, wäre Zeitverschwendung. Wenn wir argumentieren:“ Elefanten sind Säugetiere und so warmblütig“, lassen wir die Behauptung weg, dass alle Säugetiere aus diesem unschuldigen Grund warmblütig sind. ↵
- Diese Argumente haben sogar einen speziellen Namen: Sie heißen „theodicies.“↵
- Eine extrem komprimierte Version von Platons Einwänden gegen die Poesie in Buch X der Republik. ↵
- John MacFarlane verbringt in seiner vielgelesenen Doktorarbeit über 300 Seiten mit dieser Frage. Siehe: MacFarlane, J. 2000., „Was bedeutet es zu sagen, dass Logik formal ist?“Universität Pittsburgh. ↵
- Eine kurze Erklärung finden Sie im Wikipedia-Eintrag zu Paradoxien materieller Implikationen. ↵
- Eine vereinfachte version eines Arguments von Rene Descartes. ↵
Die eindeutige Bedeutung deklarativer Sätze.
Sätze, die vermitteln, dass etwas der Fall ist oder nicht. Zum Beispiel „Bob gewann die 50m Freistil.,“Deklarative Sätze können denen gegenübergestellt werden, die Fragen aufwerfen, sogenannte Fragesätze, und denen, die Befehle erteilen, die als imperative Sätze bezeichnet werden. (Deklarative Sätze werden auch als indikative Sätze bezeichnet)
Wörter, die im Allgemeinen angeben, was folgt, sind eine Prämisse, z. B. „gegeben“, „als“ „seit.“
Wörter, die im Allgemeinen darauf hinweisen, dass das Folgende eine Schlussfolgerung ist, z. B. „daher“, „so“, „folglich“.“
Argumente, die bestimmte Prämissen unbeachtet lassen.,
Räumlichkeiten, die darauf abzielen, die Wahrheit der Schlussfolgerung allein ausreichend zu unterstützen.
Prämissen, die versuchen, nicht den Abschluss eines Arguments, sondern eine andere Prämisse direkt zu unterstützen.
Prämissen, die nur die Wahrheit der Schlussfolgerung unterstützen, wenn sie kombiniert werden.