icosaedro

el icosaedro regular es uno de los cinco sólidos platónicos. Es un poliedro regular convexo compuesto de veinte caras triangulares, con cinco que se encuentran en cada uno de los Doce vértices. Tiene 30 aristas y 12 vértices. Su poliedro dual es el dodecaedro.,

Dimensions

si la longitud del borde de un icosaedro regular es , el radio de una esfera circunscrita (una que toca el icosaedro en todos los vértices) es

y el radio de una esfera inscrita (tangente a cada uno de los icosaedro las caras) es

mientras que el radio medio, que toca el Centro de cada borde, es

donde 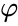(también llamado ) es la proporción áurea.,

área y volumen

el área de superficie y el volumen de un icosaedro regular de longitud de borde son:

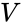
coordenadas cartesianas

Las siguientes coordenadas cartesianas definen los vértices de un icosaedro con longitud de borde 2, centrado en el origen:

donde es la proporción áurea (también escrita τ)., Tenga en cuenta que estos vértices forman cinco conjuntos de tres rectángulos dorados mutuamente centrados, mutuamente ortogonales.

las 12 aristas de un octaedro regular se pueden particionar en la proporción áurea para que los vértices resultantes definan un icosaedro regular. Esto se hace colocando primero vectores a lo largo de los bordes del octaedro de manera que cada cara esté limitada por un ciclo, y luego dividiendo de manera similar cada borde en la media dorada a lo largo de la dirección de su vector., Los cinco octaedros que definen cualquier icosaedro forman un compuesto poliédrico regular, al igual que los dos icosaedros que se pueden definir de esta manera a partir de cualquier octaedro dado.

construcción mediante un sistema de líneas equiangulares

la siguiente construcción del icoshaedron evita tediosos cálculos en el campo numérico necesarios en aproximaciones más elementales.

la existencia del icosaedro equivale a la existencia de seis líneas equiangulares en ., De hecho, la intersección de tal sistema de líneas equiangulares con una esfera euclidiana centrada en su intersección común produce los Doce vértices de un icosaedro regular como se puede comprobar fácilmente. Por el contrario, suponiendo la existencia de un icosaedro regular, las líneas definidas por sus seis pares de vértices opuestos forman un sistema equiangular.

con el fin De construir una equiángulo sistema, partimos de la matriz

de tamaño cuadrado ., (Mnemotécnica: la matriz codifica los ángulos, agudos para una entrada positiva, obtuso de lo contrario, entre cinco vértices cíclicamente consecutivos adyacente a un primer vértice de un icosaedro centrado en el origen.)

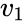
un cálculo sencillo produce . Esto implica que tiene valores propios , ambos con multiplicidad 3 ya que es simétrico y de traza 0., La matriz induce thusan Euclídea en el espacio cociente que es isomorfo a desde el kernel de tiene dimensión 3. La imagen de la proyección de los seis ejes de coordenadas en el formularios así asystem de seis equiángulo líneas en el intersección de a pares en común un ángulo agudo de ., La proyección ortogonal de sobre el – espacio propio de produce así los Doce vértices del icosaedro.

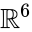
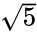
una segunda construcción directa del icosaedro utiliza la teoría de la representación del grupo alterno actuando por isometrías directas sobre el icosaedro.

Estelaciones

de acuerdo con las reglas específicas definidas en el libro los cincuenta y nueve icosaedros, se identificaron 59 estelaciones para el icosaedro regular. La primera forma es el propio icosaedro., Uno es un sólido Regular de Kepler-Poinsot. Tres son poliedros compuestos regulares.

21 de 59 estelaciones

Las caras del icosaedro extendidas hacia el exterior como los planos se cruzan, definiendo regiones en el espacio como se muestra en este diagrama de estelación de las intersecciones en un solo plano.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Estos son invariantes bajo las mismas rotaciones que el tetraedro, y son algo análogos al cubo de desaire y dodecaedro de desaire, incluyendo algunas formas que son quirales y algunas con simetría Th, es decir, tienen diferentes planos de simetría del tetraedro. El icosaedro tiene un gran número de estelaciones, incluyendo uno de los poliedros de Kepler-Poinsot y algunos de los compuestos regulares, que podrían ser discutidos aquí.

el icosaedro es único entre los sólidos platónicos en poseer un ángulo diedro no inferior a 120°. Su ángulo diédrico es de aproximadamente 138,19°.,ss que 120° y no se puede utilizar como las caras de un poliedro regular convexo porque tal construcción no cumpliría el requisito de que al menos tres caras se encuentren en un vértice y dejen un defecto positivo para el plegado en tres dimensiones, icosaedra no se puede utilizar como las células de un policorón regular convexo porque, del mismo modo, al menos tres células deben reunirse en un borde y dejar un defecto positivo para el plegado en cuatro dimensiones (en general para un politopo convexo en dimensiones, al menos tres facetas deben reunirse en un pico y dejar un defecto positivo para el plegado en n-espacio)., Sin embargo, cuando se combina con células adecuadas que tienen ángulos diédricos más pequeños, los icosaedros se pueden usar como células en polychora semi-regular (por ejemplo, el snub 24-cell), al igual que los hexágonos se pueden usar como caras en poliedros semi-regulares (por ejemplo, el icosaedro truncado). Finalmente, los politopos no convexos no tienen los mismos requisitos estrictos que los politopos convexos, y los icosaedros son de hecho las células de la célula icosaédrica 120, una de las diez policoras regulares no convexas.

un icosaedro también se puede llamar bipiramida pentagonal giroelongada., Se puede descomponer en una pirámide pentagonal giroelongada y una pirámide pentagonal o en un antiprisma pentagonal y dos pirámides pentagonales iguales.

el icosaedro también se puede llamar tetraedro de desaire, ya que la desairación de un tetraedro regular da un icosaedro regular., Alternativamente, usando la nomenclatura para poliedros desairados que se refiere a un cubo desairado como un cuboctaedro desairado (cuboctaedro = cubo rectificado) y un dodecaedro desairado como un icosidodecaedro desairado (icosidodecaedro = dodecaedro rectificado), se puede llamar al icosaedro octaedro desairado (octaedro = tetraedro rectificado).

un icosaedro rectificado forma un icosidodecaedro.

icosaedro vs dodecaedro

Cuando un icosaedro está inscrito en una esfera, ocupa menos del volumen de la esfera (60.54%) que un dodecaedro inscrito en la misma esfera (66.49%).,

además, como estos son duales, es posible transformar uno en el otro (Ver más abajo).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	en algunos juegos de rol, el dado de veinte lados (para abreviar, d20) se utiliza para determinar el éxito o el fracaso de una acción. Este dado está en la forma de un icosaedro regular. Puede ser numerada de» 0 «a» 9 » dos veces (en cuya forma generalmente sirve como un dado de diez lados, o d10), pero la mayoría de las versiones modernas están etiquetadas de «1» a «20». Ver Sistema d20.,

Un icosaedro es el juego tridimensional de la junta para Icosagame, anteriormente conocido como el Ico Cristal de Juego.

un icosaedro se utiliza en el juego de mesa Scattergories para elegir una letra del alfabeto. Seis letras poco utilizadas, como X, Q Y Z, se omiten.

dentro de una bola mágica de 8, varias respuestas a las preguntas de sí-no se imprimen en un icosaedro regular.

el icosaedro mostrado en una forma funcional se ve en el tono claro de Sol de la Flor., La roseta formada por las piezas superpuestas muestra un parecido con la flor de Frangipani.

si cada borde de un icosaedro es reemplazado por una resistencia de un ohm, La resistencia entre los vértices opuestos es de 0,5 ohmios, y La entre los vértices adyacentes de 11/30 ohmios.

el grupo de simetría del icosaedro es isomorfo al grupo alterno en cinco letras. Este grupo simple no abeliano es el único subgrupo normal no trivial del grupo simétrico en cinco letras., Dado que el grupo de Galois de la ecuación quintica general es isomorfo al grupo simétrico en cinco letras, y el hecho de que el grupo icosaédrico es simple y no abeliano significa que las ecuaciones quinticas no necesitan tener una solución en Radicales. La prueba del teorema de Abel-Ruffini utiliza este simple hecho, y Felix Klein escribió un libro que hizo uso de la teoría de las simetrías icosaédricas para derivar una solución analítica a la ecuación quintica general.,

Véase también

plantilla:Wiktionarypar

• icosaedro truncado
• poliedro regular
• las cuadrículas geodésicas utilizan un icosaedro iterativamente bisecado para generar cuadrículas en una esfera
• icosaedro de Jessen

plantilla:Wikisource1911Enc

plantilla:commonscat

• Weisstein, Eric W., «icosahedron» de MathWorld.
• modelos en papel del icosaedro
• los poliedros uniformes
• K. J. M., MacLean, a Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Interactive Icosaedron model – works right in your web browser
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Tulane.,edu es una discusión sobre la superestructura y el icosaedro
• modelos de papel de poliedros muchos enlaces
• Origami poliedros – modelos está hecho con un Origami Modular
• El video del espejo icosaédrico es una escultura

plantilla:poliedros

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl: dwudziestościan foremnypt: Icosaedrosimple:Icosahedronsq:Ikosaedri i rregulltsr:Икосаедарsv:Ikosaederta:erupted முக்கோணகம்th:.รนนาาuk: ікосаедр.