
Leonardo de Pisa (Fibonacci) (c.1170-1250)
El Siglo 13 italiano Leonardo de Pisa, mejor conocido por su apodo Fibonacci, fue quizás el más talentoso matemático Occidental de la Edad Media. Poco se sabe de su vida, excepto que era el Hijo de un funcionario de aduanas y, como un niño, viajó por el norte de África con su padre, donde aprendió sobre las matemáticas Árabes., A su regreso a Italia, ayudó a difundir este conocimiento en toda Europa, poniendo así en marcha un rejuvenecimiento en las matemáticas europeas, que habían permanecido en gran parte inactivas durante siglos durante la Edad Media.
en particular, en 1202, escribió un libro muy influyente llamado «Liber Abaci» («Libro de cálculo»), en el que promovió el uso del Sistema Numérico hindú-Arábigo, describiendo sus muchos beneficios para comerciantes y matemáticos por igual sobre el torpe sistema de números romanos entonces en uso en Europa., A pesar de sus ventajas obvias, la adopción del sistema en Europa fue lenta (esto fue después de todo durante la época de las cruzadas contra el Islam, una época en la que todo lo árabe era visto con gran sospecha), e incluso los números arábigos fueron prohibidos en la ciudad de Florencia en 1299 con el pretexto de que eran más fáciles de falsificar que los números romanos. Sin embargo, el sentido común finalmente prevaleció y el nuevo sistema fue adoptado en toda Europa en el siglo XV, haciendo que el sistema romano fuera obsoleto., La notación de barras horizontales para fracciones también se utilizó por primera vez en este trabajo (aunque siguiendo la práctica Árabe de colocar la fracción a la izquierda del entero).
Secuencia de Fibonacci

El descubrimiento de la famosa secuencia de Fibonacci
Fibonacci es mejor conocido, sin embargo, por su introducción en Europa de una secuencia de números en particular, que desde entonces se ha conocido como números de Fibonacci o la secuencia de Fibonacci., Descubrió la secuencia-la primera secuencia de números recursivos conocida en Europa – mientras consideraba un problema práctico en el» Liber Abaci » que implicaba el crecimiento de una población hipotética de conejos basada en suposiciones idealizadas. Señaló que, después de cada generación mensual, el número de pares de conejos aumentó de 1 a 2 a 3 a 5 a 8 a 13, etc., e identificó cómo progresaba la secuencia agregando los dos términos anteriores (en términos matemáticos, Fn = Fn-1 + Fn-2), una secuencia que en teoría podría extenderse indefinidamente.,
la secuencia, que en realidad había sido conocida por los matemáticos indios desde el siglo VI, tiene muchas propiedades matemáticas interesantes, y muchas de las implicaciones y relaciones de la secuencia no fueron descubiertas hasta varios siglos después de la muerte de Fibonacci., Por ejemplo, la secuencia se regenera de algunas maneras sorprendentes: cada tercer número F es divisible por 2 (F3 = 2), cada cuarto número F es divisible por 3 (F4 = 3), cada quinto número F es divisible por 5 (F5 = 5), cada sexto número F es divisible por 8 (F6 = 8), cada séptimo número F es divisible por 13 (F7 = 13), etc., Los números de la secuencia también se han encontrado ubicuos en la naturaleza: entre otras cosas, muchas especies de plantas con flores tienen números de pétalos en la secuencia de Fibonacci; los arreglos espirales de las piñas ocurren en 5s y 8s, los de las piñas en 8s y 13s, y las semillas de las cabezas de girasol en 21S, 34s, 55s o incluso en términos superiores en la secuencia; etc.,
la proporción áurea φ
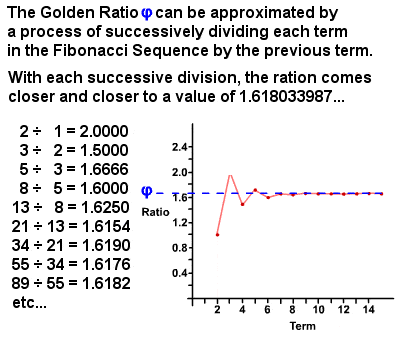
la proporción áurea φ puede derivarse de la secuencia de Fibonacci
en la década de 1750, Robert Simson observó que la proporción de cada término en la secuencia de Fibonacci con respecto al término anterior se aproxima, con mayor precisión cuanto más altos son los Términos, una proporción de aproximadamente 1 : 1.6180339887 (en realidad es un número irracional igual a (1 + √5)⁄2 que desde entonces se ha calculado a miles de decimales)., Este valor se conoce como la proporción áurea, también conocida como la media Áurea, sección áurea, proporción divina, etc., y generalmente se denota por la letra griega phi φ (o a veces La letra mayúscula Phi Φ). Esencialmente, dos cantidades están en Proporción áurea si la proporción de la suma de las cantidades a la mayor cantidad es igual a la proporción de la cantidad más grande a la más pequeña. La razón áurea en sí tiene muchas propiedades únicas, como 1⁄φ = φ – 1 (0.618…) y φ2 = φ + 1 (2.618.), y hay innumerables ejemplos de ella que se encuentran tanto en la naturaleza como en el mundo humano.,
un rectángulo con lados en la proporción de 1 : φ es conocido como un rectángulo dorado, y muchos artistas y arquitectos a lo largo de la historia (que se remonta al antiguo Egipto y Grecia, pero particularmente popular en el arte renacentista de Leonardo Da Vinci y sus contemporáneos) han proporcionado sus obras aproximadamente utilizando la proporción áurea y rectángulos dorados, que son ampliamente considerados como innatamente estéticamente agradables. Un arco que conecta puntos opuestos de rectángulos dorados anidados cada vez más pequeños forma una espiral logarítmica, conocida como espiral Dorada., La proporción áurea y la espiral Áurea también se pueden encontrar en un número sorprendente de casos en la naturaleza, desde conchas hasta flores, cuernos de animales, cuerpos humanos, Sistemas de tormentas y galaxias completas.,
debe recordarse, sin embargo, que la secuencia de Fibonacci era en realidad solo un elemento muy menor en «Liber Abaci» – de hecho, la secuencia solo recibió el nombre de Fibonacci en 1877 cuando Eduouard Lucas decidió rendirle homenaje nombrando la serie después de él – y que Fibonacci mismo no fue responsable de identificar ninguna de las propiedades matemáticas interesantes de la secuencia, su relación con la media dorada y rectángulos dorados y espirales, etc.,
multiplicación de celosías
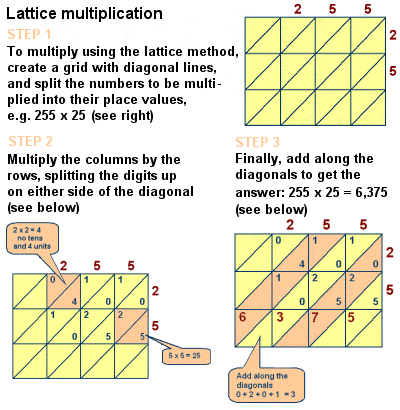
Fibonacci introdujo la multiplicación de celosías en Europa
sin embargo, la influencia del libro en las matemáticas medievales es innegable, y también incluye discusiones sobre una serie de otros problemas matemáticos como el teorema del resto Chino, números perfectos y números primos, fórmulas para series aritméticas y para números piramidales cuadrados, Euclidean geometric proofs, and a study of Simultaneous Linear Equations along the lines of diophantus And al-karaji., También describió el método de multiplicación enrejado (o tamiz) de multiplicar números grandes, un método – originalmente iniciado por matemáticos islámicos como Al-Khwarizmi – algorítmicamente equivalente a la multiplicación larga.
tampoco fue el único libro de «Liber Abaci» Fibonacci, aunque fue el más importante., Su» Liber Quadratorum «(«el Libro de los cuadrados»), por ejemplo, es un libro sobre álgebra, publicado en 1225 en el que aparece una declaración de lo que ahora se llama la identidad de Fibonacci – a veces también conocida como la identidad de Brahmagupta después de que el matemático indio mucho anterior que también llegó a las mismas conclusiones – que el producto de dos sumas de dos cuadrados es en sí mismo una suma de dos cuadrados, por ejemplo.(12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |