recientemente comencé un boletín educativo enfocado en libros. Book Dives es un boletín quincenal donde para cada nuevo número nos sumergimos en un libro de no ficción. Aprenderás sobre las lecciones principales del libro y cómo aplicarlas en la vida real. Puedes suscribirte aquí.
La agrupación en clústeres es una técnica de aprendizaje automático que implica la agrupación de puntos de datos. Dado un conjunto de puntos de datos, podemos usar un algoritmo de clustering para clasificar cada punto de datos en un grupo específico., En teoría, los puntos de datos que están en el mismo grupo deben tener propiedades y/o características similares, mientras que los puntos de datos en diferentes grupos deben tener propiedades y/o características muy diferentes. El agrupamiento es un método de aprendizaje no supervisado y es una técnica común para el análisis de datos estadísticos utilizado en muchos campos.
en Ciencia de datos, podemos usar el análisis de clústeres para obtener información valiosa de nuestros datos al ver en qué grupos caen los puntos de datos cuando aplicamos un algoritmo de clústeres., Hoy, vamos a ver 5 populares algoritmos de agrupación que los científicos de datos necesitan saber y sus pros y contras!
K-Means Clustering
k-Means es probablemente el algoritmo de clustering más conocido. Se enseña en muchas clases introductorias de ciencia de datos y aprendizaje automático. Es fácil de entender e implementar en código! Echa un vistazo al gráfico de abajo para una ilustración.,
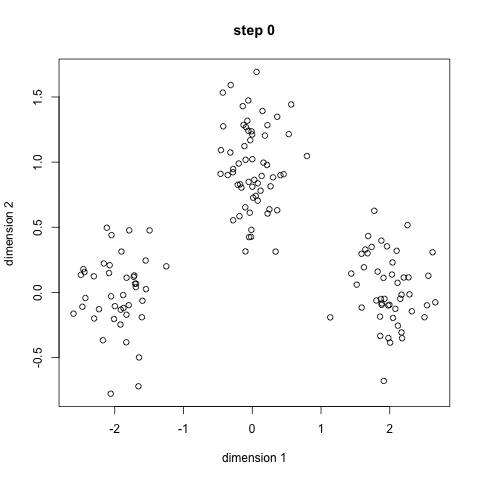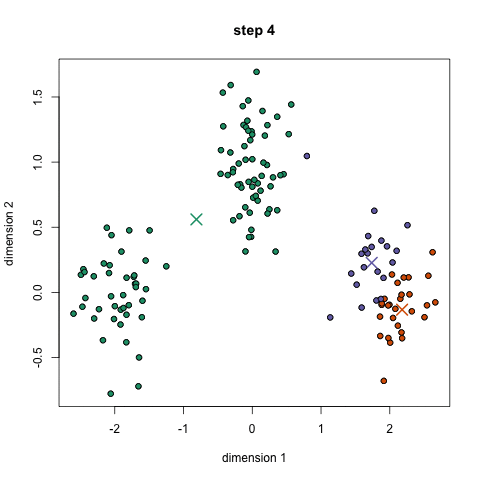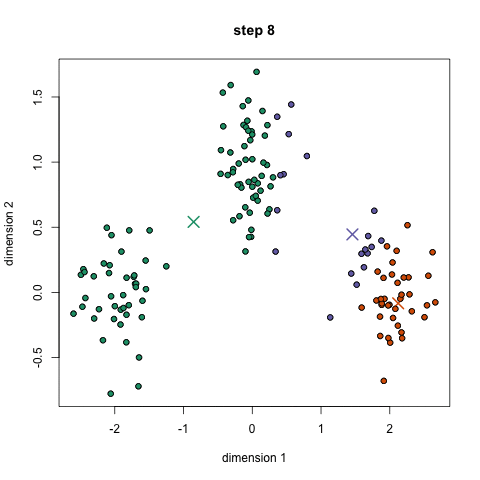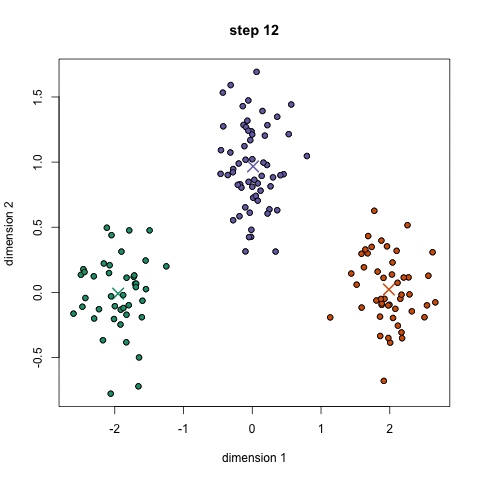
- Para comenzar, primero se debe seleccionar un número de clases/grupos a utilizar y al azar inicializar sus respectivos puntos centrales. Para averiguar el número de clases a usar, es bueno echar un vistazo rápido a los datos e intentar identificar cualquier agrupación distinta. Los puntos centrales son vectores de la misma longitud que cada vector de punto de datos y son las » X » en el gráfico de arriba.,
- Cada punto de datos se clasifica calculando la distancia entre ese punto y cada centro de grupo, y luego clasificando el punto para que esté en el grupo cuyo centro esté más cerca de él.
- basándonos en estos puntos clasificados, calculamos de nuevo el centro del grupo tomando la media de todos los vectores del grupo.
- repita estos pasos para un número determinado de iteraciones o hasta que los centros de grupo no cambien mucho entre iteraciones. También puede optar por inicializar aleatoriamente los centros de grupo unas cuantas veces y, a continuación, seleccionar la ejecución que parezca que proporcionó los mejores resultados.,
K-Means tiene la ventaja de que es bastante rápido, ya que todo lo que realmente estamos haciendo es calcular las distancias entre los puntos y los centros de grupo; ¡muy pocos cálculos! Por lo tanto, tiene una complejidad lineal O(n).
Por otro lado, K-means tiene un par de desventajas. En primer lugar, tienes que seleccionar cuántos grupos/clases hay. Esto no siempre es trivial e idealmente con un algoritmo de clustering querríamos que lo averiguara por nosotros porque el objetivo es obtener información de los datos., K-means también comienza con una elección aleatoria de centros de clúster y, por lo tanto, puede producir diferentes resultados de agrupación en diferentes ejecuciones del algoritmo. Por lo tanto, los resultados pueden no ser repetibles y carecer de consistencia. Otros métodos de clúster son más consistentes.
K-Medianas es otro algoritmo de agrupamiento relacionado con k-medias, excepto que en lugar de volver a calcular los puntos centrales del grupo utilizando la media, usamos el vector mediano del grupo., Este método es menos sensible a los valores atípicos (debido al uso de la mediana), pero es mucho más lento para conjuntos de datos más grandes, ya que se requiere ordenar en cada iteración al calcular el vector mediano.
agrupamiento de desplazamiento medio
agrupamiento de desplazamiento medio es un algoritmo basado en ventanas deslizantes que intenta encontrar áreas densas de puntos de datos. Es un algoritmo basado en centroide que significa que el objetivo es localizar los puntos centrales de cada grupo/clase, que funciona actualizando los candidatos para que los puntos centrales sean la media de los puntos dentro de la ventana deslizante., Estas ventanas candidatas se filtran en una etapa de postprocesamiento para eliminar casi duplicados, formando el conjunto final de puntos centrales y sus grupos correspondientes. Echa un vistazo al gráfico de abajo para una ilustración.
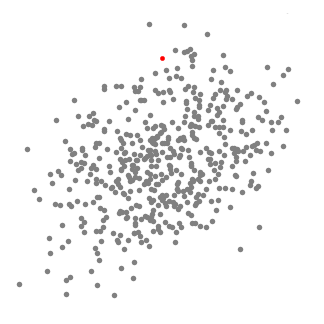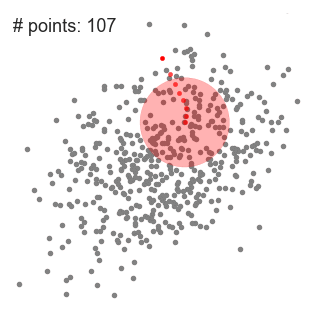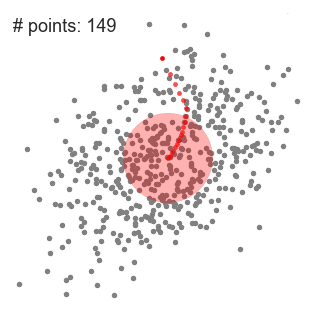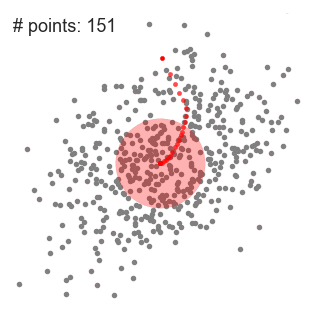
- Para explicar mean-shift vamos a considerar un conjunto de puntos en el espacio de dos dimensiones como en la ilustración de arriba., Comenzamos con una ventana deslizante circular centrada en un punto C (seleccionado aleatoriamente) y con Radio r como núcleo. Mean shift es un algoritmo de subida de colinas que implica cambiar este núcleo iterativamente a una región de mayor densidad en cada paso hasta la convergencia.
- en cada iteración, la ventana deslizante se desplaza hacia regiones de mayor densidad desplazando el punto central a la media de los puntos dentro de la ventana (de ahí el nombre). La densidad dentro de la ventana deslizante es proporcional al número de puntos dentro de ella., Naturalmente, al cambiar a la media de los puntos en la ventana, se moverá gradualmente hacia áreas de mayor densidad de puntos.
- continuamos desplazando la ventana deslizante de acuerdo con la media hasta que no haya una dirección en la que un desplazamiento pueda acomodar más puntos dentro del núcleo. Echa un vistazo al gráfico de arriba; seguimos moviendo el círculo hasta que ya no estamos aumentando la densidad (es decir, el número de puntos en la ventana).
- este proceso de pasos 1 a 3 se realiza con muchas ventanas corredizas hasta que todos los puntos se encuentran dentro de una ventana., Cuando varias ventanas correderas se superponen, se conserva la ventana que contiene la mayor cantidad de puntos. Los puntos de datos se agrupan de acuerdo con la ventana deslizante en la que residen.
Una ilustración de todo el proceso de extremo a extremo con todas las ventanas correderas se muestra a continuación. Cada punto negro representa el centroide de una ventana deslizante y cada punto gris es un punto de datos.,

En contraste con K-means clustering, no es necesario seleccionar el número de clusters como mean-shift detecta de forma automática. Esa es una gran ventaja. El hecho de que los centros de clúster converjan hacia los puntos de densidad máxima también es bastante deseable, ya que es bastante intuitivo de entender y encaja bien en un sentido naturalmente impulsado por datos., El inconveniente es que la selección del tamaño/radio de la ventana » r » puede ser no trivial.
Clustering espacial basado en densidad de aplicaciones con ruido (DBSCAN)
DBSCAN es un algoritmo clusterizado basado en densidad similar a mean-shift, pero con un par de ventajas notables. Echa un vistazo a otro gráfico de lujo a continuación y vamos a empezar!,
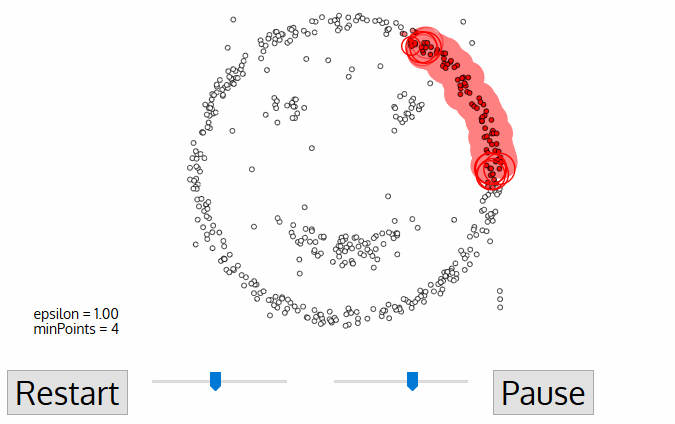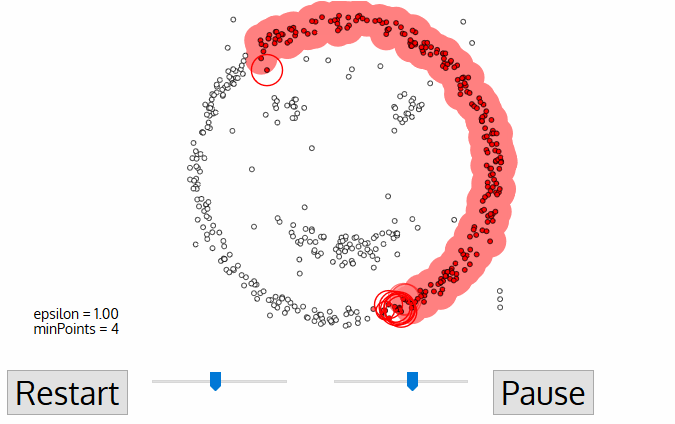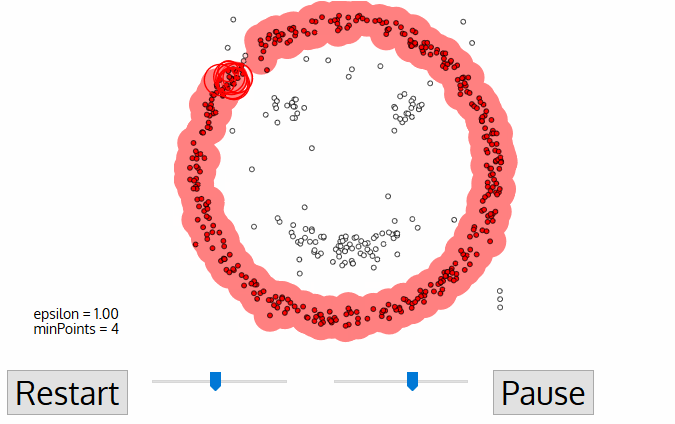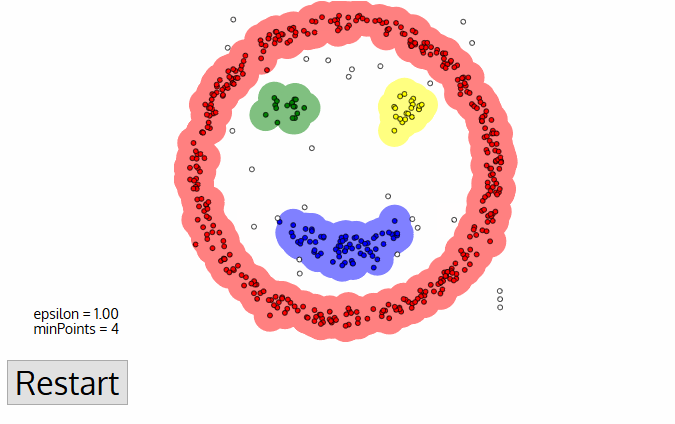
- DBSCAN comienza con una hoja de datos de partida, punto que no ha sido visitado. El vecindario de este punto se extrae usando una distancia Epsilon ε (todos los puntos que están dentro de la distancia ε son puntos de vecindario).,
- si hay un número suficiente de puntos (de acuerdo con minPoints) dentro de este vecindario, entonces el proceso de agrupación en clústeres comienza y el punto de datos actual se convierte en el primer punto del nuevo clúster. De lo contrario, el punto se etiquetará como ruido (más tarde este punto ruidoso podría convertirse en la parte del clúster). En ambos casos ese punto está marcado como»visitado».
- para este primer punto en el nuevo clúster, los puntos dentro de su vecindario de distancia ε también se convierten en parte del mismo clúster., Este procedimiento de hacer que todos los puntos en el vecindario ε pertenezcan al mismo clúster se repite para todos los nuevos puntos que se acaban de agregar al grupo de clúster.
- este proceso de los pasos 2 y 3 se repite hasta que se determinen todos los puntos en el clúster, es decir, todos los puntos dentro del vecindario ε del clúster han sido visitados y Etiquetados.
- Una vez que hemos terminado con el clúster actual, se recupera y procesa un nuevo punto no visitado, lo que conduce al descubrimiento de un clúster o ruido adicional. Este proceso se repite hasta que todos los puntos se marcan como visitados., Dado que al final de esto se han visitado todos los puntos, cada punto se habrá marcado como perteneciente a un clúster o como ruido.
DBSCAN presenta grandes ventajas sobre otros algoritmos de clustering. En primer lugar, no requiere un número pe-set de clusters en absoluto. También identifica los valores atípicos como ruidos, a diferencia de mean-shift, que simplemente los arroja a un clúster incluso si el punto de datos es muy diferente. Además, puede encontrar racimos arbitrariamente dimensionados y arbitrariamente formados bastante bien.,
el principal inconveniente de DBSCAN es que no funciona tan bien como otros cuando los clústeres son de densidad variable. Esto se debe a que la configuración del umbral de distancia ε y minPoints para identificar los puntos de vecindad variará de un clúster a otro cuando la densidad varíe. Este inconveniente también ocurre con datos de dimensiones muy altas, ya que nuevamente el umbral de distancia ε se vuelve difícil de estimar.,
agrupamiento de maximización de expectativas (EM) utilizando modelos de mezcla Gaussiana (GMM)
uno de los principales inconvenientes de K-Means es su uso ingenuo del valor medio para el centro del clúster. Podemos ver por qué esta no es la mejor manera de hacer las cosas mirando la imagen de abajo. En el lado izquierdo, parece bastante obvio para el ojo humano que hay dos cúmulos circulares con diferentes radios centrados en la misma media. K-Means no puede manejar esto porque los valores medios de los clústeres están muy cerca entre sí., K-Means también falla en los casos en que los clústeres no son circulares, de nuevo como resultado de usar la media como centro del clúster.

Gaussian mixture models (Mgm) nos dará más flexibilidad de K-Means. Con GMMs asumimos que los puntos de datos son gaussianos distribuidos; esto es una suposición menos restrictiva que decir que son circulares usando la media., De esta manera, Tenemos dos parámetros para describir la forma de los grupos: la media y la desviación estándar! Tomando un ejemplo en dos dimensiones, esto significa que los grupos pueden tomar cualquier tipo de forma elíptica (ya que tenemos una desviación estándar en las direcciones x E y). Por lo tanto, cada distribución gaussiana se asigna a un solo clúster.
para encontrar los parámetros del gaussiano para cada clúster (por ejemplo, la media y la desviación estándar), usaremos un algoritmo de optimización llamado expectativa–maximización (EM)., Echa un vistazo al gráfico de abajo como una ilustración de las gaussianas que se ajustan a los grupos. Luego podemos proceder con el proceso de agrupamiento de maximización de expectativas utilizando GMMs.
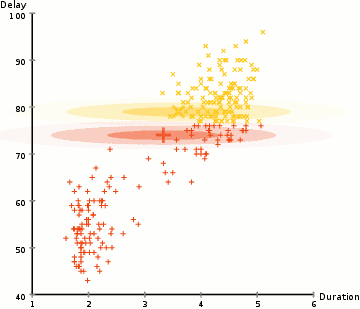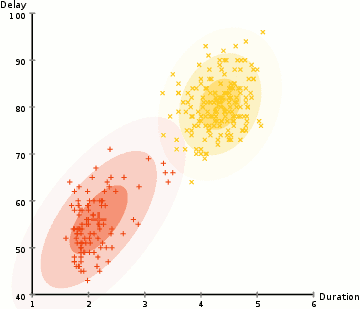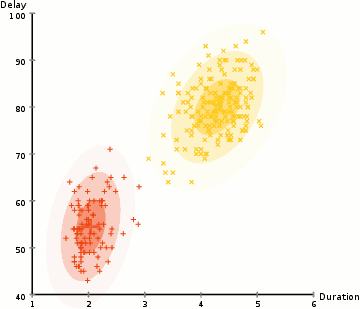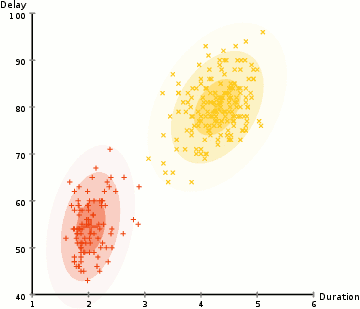
- Comenzamos seleccionando el número de clusters (como K-means hace) y al azar la inicialización de la distribución Gaussiana de los parámetros para cada clúster., Uno puede tratar de proporcionar una buena estimación de los parámetros iniciales echando un vistazo rápido a los datos también. Aunque tenga en cuenta, como se puede ver en el gráfico de arriba, esto no es 100% necesario como los Gaussians empezar nuestra como muy pobre, pero se optimizan rápidamente.
- dadas estas distribuciones gaussianas para cada clúster, calcule la probabilidad de que cada punto de datos pertenezca a un clúster en particular. Cuanto más cerca esté un punto del centro gaussiano, más probable será que pertenezca a ese cúmulo., Esto debería tener sentido intuitivo ya que con una distribución gaussiana estamos asumiendo que la mayoría de los datos se encuentran más cerca del centro del clúster.
- basado en estas probabilidades, calculamos un nuevo conjunto de parámetros para las distribuciones gaussianas de tal manera que maximizamos las probabilidades de los puntos de datos dentro de los clústeres. Calculamos estos nuevos parámetros utilizando una suma ponderada de las posiciones de los puntos de datos, donde los pesos son las probabilidades del punto de datos que pertenece a ese clúster en particular., Para explicar esto visualmente podemos echar un vistazo al gráfico de arriba, en particular al cluster amarillo como ejemplo. La distribución comienza aleatoriamente en la primera iteración, pero podemos ver que la mayoría de los puntos amarillos están a la derecha de esa distribución. Cuando calculamos una suma ponderada por las probabilidades, aunque hay algunos puntos cerca del centro, la mayoría de ellos están a la derecha. Así, naturalmente, la media de la distribución se desplaza más cerca de ese conjunto de puntos. También podemos ver que la mayoría de los puntos son «arriba-derecha a abajo-izquierda»., Por lo tanto, la desviación estándar cambia para crear una elipse que se ajuste más a estos puntos, para maximizar la suma ponderada por las probabilidades.
- Los Pasos 2 y 3 se repiten iterativamente hasta la convergencia, donde las distribuciones no cambian mucho de iteración a iteración.
Hay 2 ventajas clave al usar GMMs. En primer lugar, los GMM son mucho más flexibles en términos de covarianza de clústeres que las medias K; debido al parámetro de desviación estándar, los clústeres pueden tomar cualquier forma de elipse, en lugar de restringirse a círculos., K-Means es en realidad un caso especial de GMM en el que la covarianza de cada clúster a lo largo de todas las dimensiones se acerca a 0. En segundo lugar, dado que los MMG utilizan probabilidades, pueden tener múltiples clústeres por punto de datos. Así que si un punto de datos está en el medio de dos clústeres superpuestos, podemos simplemente definir su clase diciendo que pertenece X-por ciento a la clase 1 y y-por ciento a la clase 2. Es decir, el MMG apoya la membresía mixta.
agrupamiento jerárquico Aglomerativo
los Algoritmos de agrupamiento jerárquico se dividen en 2 categorías: de arriba hacia abajo o de abajo hacia arriba., Los algoritmos Bottom-up tratan cada punto de datos como un solo clúster al principio y luego fusionan (o aglomeran) sucesivamente pares de clústeres hasta que todos los clústeres se han fusionado en un solo clúster que contiene todos los puntos de datos. Por lo tanto, la agrupación jerárquica ascendente se denomina agrupación aglomerativa jerárquica o HAC. Esta jerarquía de clusters se representa como un árbol (o dendrograma). La raíz del árbol es el único racimo que reúne todas las muestras, siendo las hojas los racimos con una sola muestra., Consulte el gráfico a continuación para obtener una ilustración antes de pasar a los pasos del algoritmo
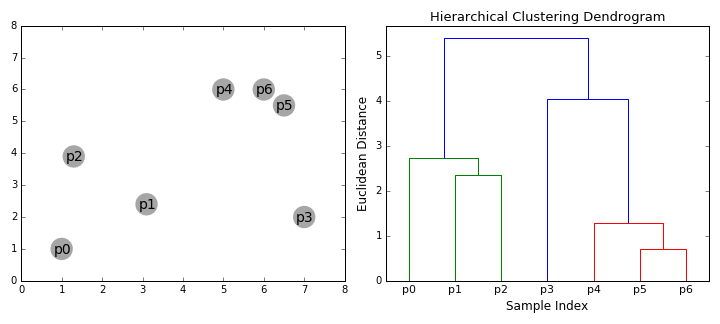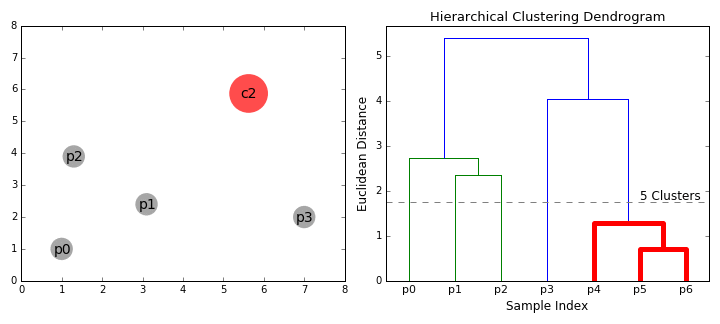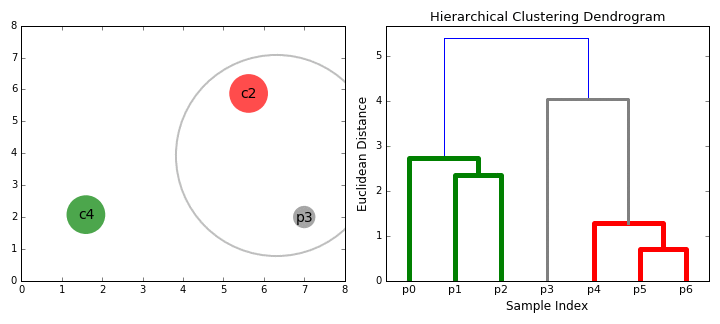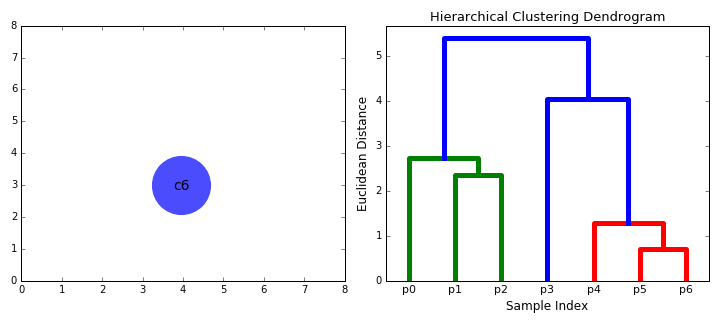
- comenzamos tratando cada punto de datos como un solo clúster, es decir, si hay X puntos de datos en nuestro conjunto de datos, entonces tenemos X clústeres. Luego seleccionamos una métrica de distancia que mide la distancia entre dos clústeres., Como ejemplo, usaremos el enlace promedio que define la distancia entre dos clústeres como la distancia promedio entre los puntos de datos en el primer clúster y los puntos de datos en el segundo clúster.
- En cada iteración, combinamos dos clústeres en uno. Los dos grupos que se combinarán se seleccionan como los que tienen el enlace medio más pequeño. Es decir, de acuerdo con nuestra métrica de distancia seleccionada, estos dos clústeres tienen la distancia más pequeña entre sí y, por lo tanto, son los más similares y deben combinarse.
- El Paso 2 se repite hasta llegar a la raíz del árbol i.,e solo tenemos un clúster que contiene todos los puntos de datos. De esta manera podemos seleccionar cuántos clústeres queremos al final, simplemente eligiendo cuándo dejar de combinar los clústeres, es decir, cuando dejemos de construir el árbol.
la agrupación jerárquica en clústeres no requiere que especifiquemos el número de clústeres e incluso podemos seleccionar qué número de clústeres se ve mejor ya que estamos construyendo un árbol. Además, el algoritmo no es sensible a la elección de la métrica de distancia; todos ellos tienden a funcionar igual de bien, mientras que con otros algoritmos de agrupamiento, la elección de la métrica de distancia es crítica., Un caso de uso particularmente bueno de los métodos de agrupamiento jerárquico es cuando los datos subyacentes tienen una estructura jerárquica y desea recuperar la jerarquía; otros algoritmos de agrupamiento no pueden hacer esto. Estas ventajas de la agrupación jerárquica vienen en el costo de menor eficiencia, ya que tiene una complejidad de tiempo de o(n3), a diferencia de la complejidad lineal de k-medias y GMM.