resultados de aprendizaje
- familiarícese con la historia de los sistemas numéricos posicionales
- identifique las bases que se han utilizado en sistemas numéricos históricamente
- convierta números entre bases
- Use dos métodos diferentes para convertir números entre bases
omo se puede imaginar, el desarrollo de un sistema base es un paso importante para hacer que el proceso de conteo sea más eficiente., Nuestro propio sistema base-diez probablemente surgió del hecho de que tenemos 10 dedos (incluidos los pulgares) en dos manos. Este es un desarrollo natural. Sin embargo, otras civilizaciones han tenido una variedad de bases con excepción de diez. Por ejemplo, los nativos de Queensland usaron un sistema base-dos, contando de la siguiente manera: «uno, dos, dos y uno, dos, dos, mucho.»Algunas tribus Sudamericanas modernas tienen un sistema base-cinco que cuenta de esta manera: «uno, dos, tres, cuatro, mano, mano y uno, mano y dos», y así sucesivamente. Los babilonios usaban un sistema de base sesenta (sexigesimal)., En este capítulo, concluimos con un ejemplo específico de una civilización que realmente utilizó un sistema base que no sea 10.
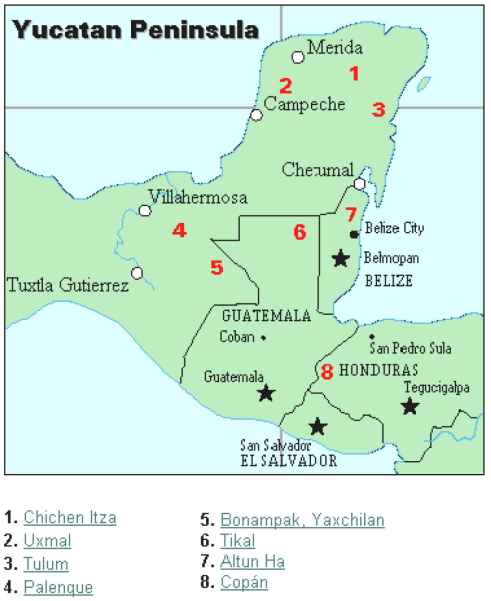 la civilización maya generalmente data de 1500 A.C. a 1700 D. C. La Península de Yucatán (ver Figura 16) en México fue el escenario para el desarrollo de una de las civilizaciones más avanzadas del mundo antiguo. Los mayas tenían un sofisticado sistema ritual que era supervisado por una clase sacerdotal. Esta clase de sacerdotes desarrolló una filosofía con el tiempo como divino y eterno., El calendario, y los cálculos relacionados con él, eran por lo tanto muy importantes para la vida ritual de la clase sacerdotal, y por lo tanto del Pueblo Maya. De hecho, mucho de lo que sabemos sobre esta cultura proviene de sus registros de calendario y datos astronómicos. Otra fuente importante de información sobre los mayas son los escritos del Padre Diego de Landa, que fue a México como misionero en 1549.
la civilización maya generalmente data de 1500 A.C. a 1700 D. C. La Península de Yucatán (ver Figura 16) en México fue el escenario para el desarrollo de una de las civilizaciones más avanzadas del mundo antiguo. Los mayas tenían un sofisticado sistema ritual que era supervisado por una clase sacerdotal. Esta clase de sacerdotes desarrolló una filosofía con el tiempo como divino y eterno., El calendario, y los cálculos relacionados con él, eran por lo tanto muy importantes para la vida ritual de la clase sacerdotal, y por lo tanto del Pueblo Maya. De hecho, mucho de lo que sabemos sobre esta cultura proviene de sus registros de calendario y datos astronómicos. Otra fuente importante de información sobre los mayas son los escritos del Padre Diego de Landa, que fue a México como misionero en 1549.
 había dos sistemas numéricos desarrollados por los Mayas—uno para la gente común y otro para los sacerdotes., Estos dos sistemas no solo usaban símbolos diferentes, sino que también usaban sistemas base diferentes. Para los sacerdotes, el sistema numérico se regía por rituales. Los días del año se pensaba que eran dioses, por lo que los símbolos formales para los días eran cabezas decoradas, como la muestra a la izquierda ya que el calendario básico se basa en 360 días, el sistema de numeración sacerdotal utiliza un sistema de base mixta empleando múltiplos de 20 y 360. Esto lo convierte en un sistema confuso, cuyos detalles omitiremos.,/td>
había dos sistemas numéricos desarrollados por los Mayas—uno para la gente común y otro para los sacerdotes., Estos dos sistemas no solo usaban símbolos diferentes, sino que también usaban sistemas base diferentes. Para los sacerdotes, el sistema numérico se regía por rituales. Los días del año se pensaba que eran dioses, por lo que los símbolos formales para los días eran cabezas decoradas, como la muestra a la izquierda ya que el calendario básico se basa en 360 días, el sistema de numeración sacerdotal utiliza un sistema de base mixta empleando múltiplos de 20 y 360. Esto lo convierte en un sistema confuso, cuyos detalles omitiremos.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the «common” people, which used a more consistent base system., Como dijimos anteriormente, los Mayas usaron un sistema base-20, llamado el sistema «vigesimal». Al igual que nuestro sistema, es posicional, lo que significa que la posición de un símbolo numérico indica su valor de posición. En la siguiente tabla puede ver el valor de posición en su formato vertical.
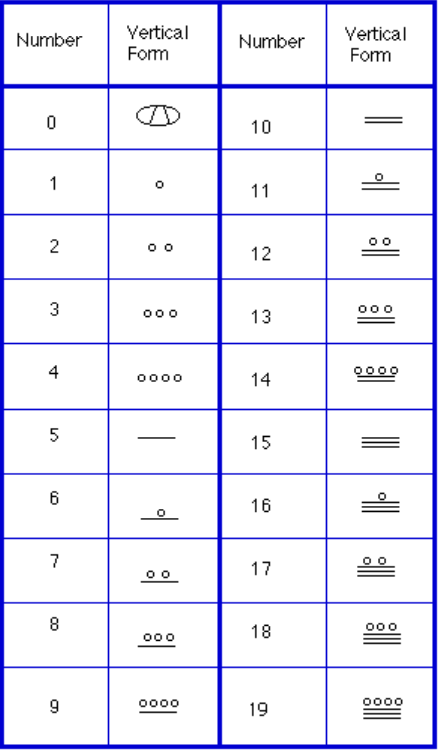
para escribir números, solo se necesitaban tres símbolos en este sistema. Una barra horizontal representaba la cantidad 5, un punto representaba la cantidad 1, y un símbolo especial (que se cree que es una cáscara) representaba el cero., El sistema Maya puede haber sido el PRIMERO en hacer uso del cero como marcador de posición/número. Los primeros 20 números se muestran en la tabla de la derecha.
a diferencia de nuestro sistema, donde el lugar de las unidades comienza a la derecha y luego se mueve a la izquierda, los sistemas Mayas colocan las unidades en la parte inferior de una orientación vertical y se mueve hacia arriba a medida que aumenta el valor del lugar.
cuando los números se escriben en forma vertical, nunca debe haber más de cuatro puntos en un solo lugar. Al escribir números Mayas, cada grupo de cinco puntos se convierte en una barra., Además, nunca debe haber más de tres barras en un solo lugar…cuatro barras de ser convertido a un punto en el siguiente lugar. Es lo mismo que 10 convertirse en un 1 en el siguiente lugar cuando llevamos durante la adición.
Ejemplo
¿Cuál es el valor de este número, que se muestra en forma vertical?
Ejemplo
¿Cuál es el valor de la siguiente Maya número?,
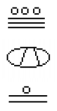
pruébelo
convierta el número Maya de abajo a base 10.,

Ejemplo
Convertir la base 10 el número de 357510 a Maya números.
tenga en cuenta que en el ejemplo anterior se utilizó una nueva Notación cuando escribimos 8,18,1520. Las comas entre los tres números 8, 18 y 15 ahora están separando los valores de lugar para nosotros para que podamos mantenerlos separados entre sí. Este uso de la coma es ligeramente diferente de cómo se utilizan en el sistema decimal. Cuando escribimos un número en base 10, como 7,567,323, las comas se usan principalmente como ayuda para leer el número fácilmente, pero no separan los valores de un solo lugar entre sí., Necesitaremos esta notación siempre que la base que utilicemos sea mayor que 10.
escribir números con bases mayores que 10
Cuando la base de un número es mayor que 10, separe cada «dígito» con una coma para que la separación de dígitos sea clara.
por ejemplo, en base 20, para escribir el número correspondiente a 17 × 202 + 6 × 201 + 13 × 200, escribiríamos 17,6,1320.
en el siguiente video presentamos más ejemplos de cómo escribir números usando números Mayas, así como convertir números escritos en Maya para en forma de base 10.,
el siguiente video muestra más ejemplos de convertir números base 10 en números Mayas.
agregar números Mayas
al agregar números Mayas juntos, adoptaremos un esquema que los Mayas probablemente no usaron, pero que nos hará la vida un poco más fácil.
Ejemplo
Añadir, en Maya, los números 37 y 29:

pruébelo
intente agregar 174 y 78 en Mayan primero convirtiendo a números Mayas y luego trabajando completamente dentro de ese sistema. No agregue en base diez (decimal) hasta el final cuando revise su trabajo.
En el último vídeo nos muestran más ejemplos de la adición de Maya números.,
en este módulo, hemos esbozado brevemente el desarrollo de los números y nuestro sistema de conteo, con el énfasis en la parte «breve». Hay numerosas fuentes de información e investigación que llenan muchos volúmenes de libros sobre este tema. Desafortunadamente, no podemos empezar a acercarnos a cubrir toda la información que está ahí fuera.

solo hemos arañado la superficie de la riqueza de la investigación y la información que existe sobre el desarrollo de los números y el conteo a lo largo de la historia humana., Lo que es importante tener en cuenta es que el sistema que utilizamos todos los días es un producto de miles de años de progreso y desarrollo. Representa las contribuciones de muchas civilizaciones y culturas. No nos llega del cielo, un regalo de los dioses. No es la creación de un editor de libros de texto. De hecho, es tan humano como nosotros, como lo es el resto de las matemáticas. Detrás de cada símbolo, fórmula y regla hay un rostro humano que se encuentra, o al menos se busca.
Además, esperamos que ahora tenga una apreciación básica de lo interesante y diverso que pueden ser los sistemas numéricos., Además, estamos bastante seguros de que también han comenzado a reconocer que damos por sentado nuestro propio sistema numérico tanto que cuando tratamos de adaptarnos a otros sistemas o bases, nos encontramos realmente teniendo que concentrarnos y pensar en lo que está pasando.







