Midiendo la constante de Rydberg

Introducción

en este experimento, observará las longitudes de onda visibles de la luz producida por una descarga eléctrica en gas de helio, utilizando una rejilla de difracción. A partir del conocimiento de los valores de longitud de onda, podrá calibrar con precisión el espaciado de línea de la rejilla de difracción. Una vez calibrada, la rejilla se utiliza para medir la longitud de onda de la luz producida por el hidrógeno atómico. Al realizar un ajuste de curva a estas longitudes de onda medidas, puede determinar la constante de Rydberg, una constante física importante., Este es un experimento en el que la técnica cuidadosa y la medición darán sus frutos: debería ser capaz de determinar la constante de Rydberg dentro del uno por ciento o mejor. Los gases de helio e hidrógeno están contenidos en tubos de descarga de baja presión que tienen electrodos metálicos en cada extremo. Cuando se aplica un alto voltaje a través de los dos electrodos, una corriente eléctrica fluye a través del gas. Los electrones de alta energía en la corriente eléctrica chocan con los átomos de gas y, en el proceso, pueden impartir energía interna a los átomos., Estos átomos excitados pueden entonces liberar energía en forma de radiación electromagnética en longitudes de onda específicas. Parte de esta radiación electromagnética está en el rango visible.Un profesor Suizo llamado Johann Balmer (1825 – 1898) estudió las longitudes de onda de la luz visible emitida por los átomos de hidrógeno. Encontró una ecuación empírica que coincide exactamente con los valores de las longitudes de onda observadas.,

n = 3, 4, 5,Aquí R es la constante de Rydberg 1, que ha sido precisamente medido y el valor R = 10973731.5683 ± 0.0003 m–1. La variable n es cualquier entero igual o mayor que 3. La serie de longitudes de onda que resultan de n = 3, 4, 5, …, se llama la serie Balmer.,1 la teoría cuántica moderna de la estructura atómica predice el valor de R en términos de otras constantes fundamentales: c (Velocidad de la luz), h (constante de Planck), e (carga del electrón) y m (masa del electrón). El valor medido experimentalmente de R dado arriba concuerda con la predicción teórica dentro de las incertidumbres combinadas de estas otras constantes fundamentales, dando así credibilidad a la teoría. Este es un buen ejemplo de donde el análisis de errores es clave para ayudarnos a determinar si una teoría en física realmente describe la naturaleza.,Se puede utilizar una rejilla de difracción para observar las longitudes de onda individuales de la luz emitida desde el tubo de descarga. La rejilla que utilizará tiene una densidad de línea o ranura de aproximadamente 300 líneas / mm, por lo que el espaciado de línea d es del orden de 3 × 10-6 m. a medida que la luz de longitud de onda λ del tubo de descarga pasa a través de la rejilla, se difracta a través de un ángulo, θ, dado por la ecuación de rejilla.

aquí m es un entero y se llama el orden de la difracción., Para la rejilla que va a utilizar, ellos = ± 1 y m = ± 2 órdenes serán fácilmente observables.La disposición experimental vista desde arriba se muestra en la Figura 1. Se ve la luz del tubo de descarga mirando a través de la rejilla de difracción. A los lados izquierdo y derecho del tubo, debe poder ver imágenes en color del tubo de descarga que aparecen por encima y por debajo de la barra del medidor. La figura 2 muestra la vista vista a través de la rejilla.,

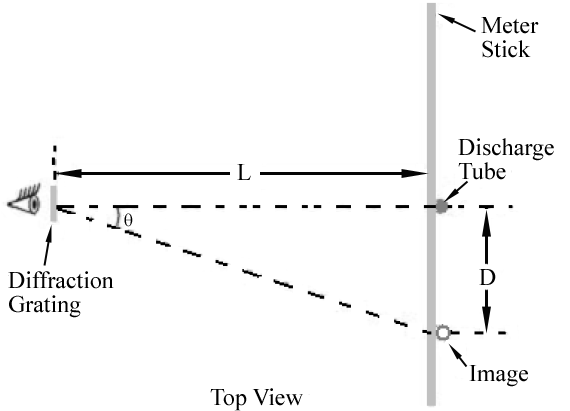
Figura 1.

Como se muestra en la Figura 1, el primer orden de la imagen para cada longitud de onda aparecerá en un ángulo θ, la satisfacción de Eq. (2)

. Por lo tanto, diferentes longitudes de onda aparecerán en diferentes lugares a lo largo de la barra del medidor. El ángulo correspondiente a cada longitud de onda se puede determinar midiendo D y L.

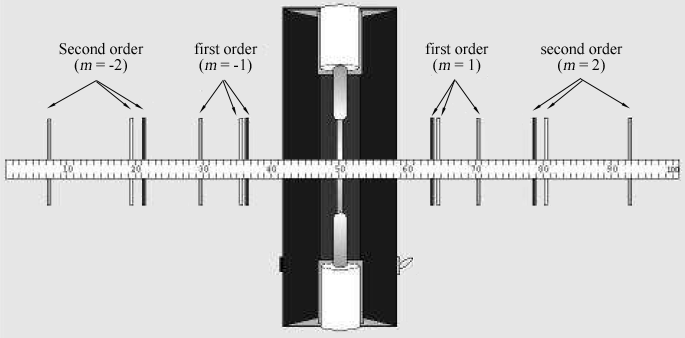
Figura 2: líneas espectrales vistas a través de la rejilla de difracción a un metro de un tubo de descarga.

si λ y θ se conocen en la EC., (2)

mλ = D sin θ

, entonces d puede ser determinado. Medirás θ Para siete longitudes de onda conocidas en helio. Un ajuste de curva le permitirá determinar con precisión el espaciado de la rejilla d.en la segunda parte del laboratorio, utilizará este valor de d para medir con precisión las longitudes de onda en hidrógeno.

Procedimiento

Precaución:
extreme la precaución en el tubo de descarga de la fuente de alimentación. Produce 5000 voltios con corriente suficiente para ser peligroso. No toque los electrodos de suministro ni el tubo mientras el suministro está encendido., Apague la fuente de alimentación cuando cambie los tubos de descarga. Dado que el área se calienta mucho durante el uso, evite agarrar el Centro de los tubos.

Parte 1: Helio Espectro

1

Configurar el arreglo se muestra en la Figura 1. Asegúrese de que la fuente de alimentación del tubo de descarga esté desenchufada y apagada. Inserte un tubo de gas de helio en los soportes del electrodo. (Los tubos son frágiles; por favor, manipúlelos con cuidado.) El tubo debe estar recto hacia arriba y hacia abajo y posicionado cerca de la marca de 50 cm en el palillo del medidor.,

2

Conecte y encienda la fuente de alimentación. El tubo de descarga debe encenderse inmediatamente. Si no es así, pídale ayuda al instructor. Un compañero de laboratorio debe mirar a través de la rejilla de difracción mientras que el otro compañero trabaja en el lado opuesto de la barra del medidor tomando lecturas.

3

la persona que mira a través de la rejilla de difracción debe mirar a la izquierda y a la derecha del tubo de descarga para localizar las imágenes de difracción. Localice las imágenes de primer orden

(m = ± 1)

y de segundo orden

(m = ± 2)

., Si es necesario, gire la rejilla para que las imágenes aparezcan justo por encima y por debajo de la barra del medidor de la misma manera que lo hace el tubo de descarga.

4

la tabla 1 enumera las longitudes de onda de siete de las líneas visibles más brillantes en el espectro de helio en el orden de la longitud de onda más corta a más larga. Las imágenes para cada orden de difracción aparecerán en este mismo orden, con la longitud de onda más pequeña en el ángulo más pequeño. Empareja las imágenes con las longitudes de onda listadas. Mirando a través de la rejilla a la derecha, localice la posición de la primera imagen a lo largo del palillo del medidor., El compañero de laboratorio que mire a través de la rejilla debe instruir al otro compañero de laboratorio para colocar un pequeño puntero (por ejemplo, un lápiz) a lo largo del palo del medidor hasta que el puntero esté en línea con la imagen que se está midiendo. El socio con el puntero entonces lee la posición a lo largo del palillo del metro. Use una lámpara de lectura de baja potencia si es necesario para leer el medidor. Anote la posición XR de cada una de las líneas de helio en la tabla 1.

5

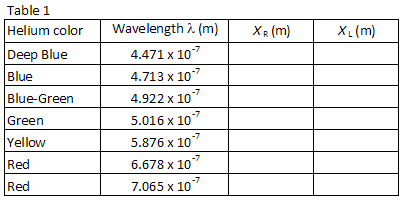
Repita el proceso para las siete imágenes que aparecen a la izquierda del tubo de descarga., Registre la posición XL de cada imagen en la tabla 1.

Parte 2: espectro de hidrógeno

1

apague y desenchufe la fuente de alimentación de descarga y permita que el tubo de descarga se enfríe durante varios minutos. (Precaución: el tubo estará muy caliente la primera vez que apague el suministro.) Retire el tubo de helio y reemplácelo con el tubo de hidrógeno. Vuelva a colocar la fuente de alimentación con el tubo de hidrógeno en la posición de 50 cm a lo largo de la barra del medidor.

2

tres colores fácilmente observados en hidrógeno se enumeran en la Tabla 2., Haga coincidir los colores con las imágenes vistas a través de la rejilla de difracción. Registre las posiciones XR y XL de las imágenes de primer orden en la Tabla 2.

3

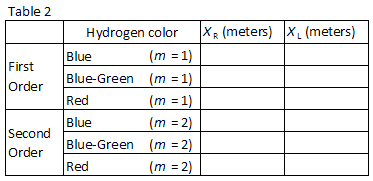
Sin perturbar el medidor de palo o una rejilla de difracción, medir cuidadosamente la distancia L en la Figura 1, utilizando una métrica cinta métrica. Incluya la incertidumbre en su valor registrado.,

análisis

espaciado de rejilla d

1

para cada longitud de onda de helio, calcule la distancia promedio entre el tubo de descarga y las imágenes de primer orden utilizando la siguiente ecuación.

( 3 )

D =

XR − XL

2

También calcular

tan θ =

D

L

, θ,

y sen θ para cada longitud de onda. Registre sus cálculos en la Tabla 3.

3

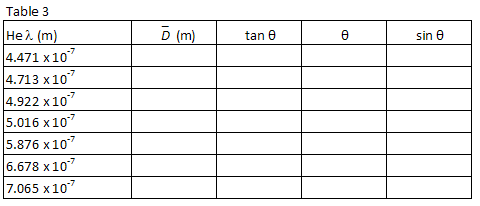
Parcela λ vs, sin θ y, usando un ajuste lineal al menos cuadrado, encontrar la pendiente. A partir de la pendiente de su gráfico, encuentre su mejor estimación para el espaciado de la rejilla, d, en metros y el error estimado en d.

constante de Rydberg

1

siguiendo el mismo procedimiento utilizado en el paso 1 anterior, encuentre Sin θ para cada una de las longitudes de onda de hidrógeno que observó y regístrelas en la Tabla 4.

2

Usando el valor para el espaciado de rejilla encontrado en el paso 2 anterior y la ecuación de rejilla, EC., (2)

mλ = D sin θ

, calcular la longitud de onda, en metros, de las tres líneas de hidrógeno observadas y registrarlas en la Tabla 4.

4

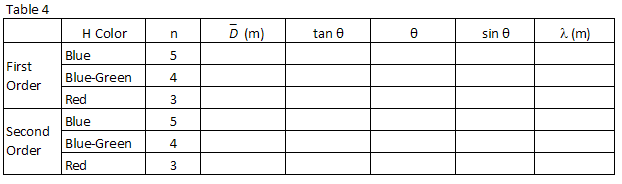
Realizar un ajuste lineal por mínimos cuadrados a los datos.

5

Eq. (1)

λ

= R

−

n2

n = 3, 4, 5,

puede ser reescrita de la siguiente forma.,

discusión

resuma sus resultados para el valor del espaciado de la rejilla y la constante de Rydberg (tanto sus valores como sus incertidumbres)., Compare cuantitativamente su valor para la constante de Rydberg con el valor aceptado R = 10973732 m-1.