distribuciones
El problema principal en el corazón de los problemas con el delta de Dirac y objetos matemáticos similares es el problema de la diferenciabilidad. Como Dirac declaró en la cita anterior, realmente no te metes en problemas si usas su función δ como una regla simbólica de cómo actúa sobre otras funciones; sin embargo, él procede a diferenciar δ en sus cálculos, y aquí es donde los problemas realmente comienzan., ¿Cómo se puede saber a priori «cuando estas operaciones son permisibles» cuando ni siquiera se tiene una definición firme de los objetos, o lo que significaría diferenciarlos? Veremos cómo estas preguntas conducen a la derivación de nuevos objetos matemáticos rigurosamente definidos.
funcionales
considere cómo se determina normalmente la derivada (o antiderivada) de una función. En circunstancias normales, con funciones «clásicas», tiene una regla bien definida que describe cómo una función asigna un conjunto de números reales a otro conjunto, digamos f:→→→., Dado esto y las definiciones de la integral o derivada, uno puede entonces investigar claramente los valores que estos operadores rinden cuando se aplican a la función. En el caso de δ, No tenemos una definición viable para proceder a lo largo de estas líneas. En cambio, en la práctica δ se define más prominentemente por cómo opera en otras funciones bien definidas (como en (3)). Esta es la visión clave que conduce a la teoría moderna de las distribuciones. Resulta que la forma correcta de tratar matemáticamente δ, y una gran clase de objetos similares, es dejar de intentar definir como funciones., Esta línea de pensamiento es bien descrita por Jean Dieudonne en su revisión de (ver ):
one uno comienza con una familia de funciones muy «regulares» (generalmente con
respecto a propiedades diferenciales), que satisfacen ciertas relaciones (generalmente
integrales), o en las que ciertas operaciones son posibles; y
entonces uno descubre que una familia a priori más grande de funciones satisface
las mismas relaciones, o puede ser sometida a operaciones similares. Muchas preguntas entonces pueden ser hechas naturalmente: ¿es esta nueva familia realmente diferente de la primera?, Si lo es, ¿cuáles son las relaciones entre las dos familias, y se puede dar una descripción precisa de la nueva?
es solo en la última etapa de la » prehistoria «que emergerá lo que puede llamarse un punto de vista revolucionario, con la idea de que
la» nueva familia » podría consistir en objetos que no sean funciones.
Los otros objetos a los que se alude son funcionales. Puedes pensar en un
funcional como una función de funciones., Como una función es una asignación única de un conjunto de números
a otro, una f funcional se puede definir como una asignación F: C→
donde C es un conjunto de funciones. Es decir, una función mapea funciones a números reales
., Un ejemplo sencillo de un funcional de este tipo es el de la integral definida:

que toma claramente una función f de un conjunto de adecuada integración de las funciones y la asigna a un número real, el valor de la integral, o el área bajo la curva de f(x) entre a y b. Este es un solo ejemplo., Uno puede imaginar un número infinito de funcionales, y conjuntos de funcionales; uno podría incluso continuar generalizando y definiendo asignaciones de conjuntos de funcionales a números reales. Eso no es ni aquí ni allá. Lo importante es que el concepto funcional se puede utilizar para definir distribuciones.
El conjunto de funciones de prueba
requerimos una definición más para lograr nuestro objetivo. Esto equivale a especificar el conjunto C de funciones desde el cual las distribuciones mapearán funciones a números reales., Las funciones a menudo se recogen en conjuntos que especifican su grado de continuidad, diferenciabilidad y la continuidad de sus derivadas. Decimos que una función f está en el conjunto C ∈ (escribe f ∈ C.) si es continua sobre toda la recta real en el sentido de que el límite en todos los puntos es el mismo cuando se toma de la izquierda o de la derecha; no es necesariamente diferenciable. Decimos que f ∈ C1 si su derivada existe y es continua, es decir, f ‘ ∈ C⁰. Por ejemplo, la función g(x) = |x| es continua pero no derivable en x= 0; g C⁰ pero no en C1., Podemos generalizar esto y decir que C is es el conjunto de funciones que tienen para funciones continuas sus primeras derivadas n, donde n es un entero.
a medida que n se hace más grande, los conjuntos se vuelven en cierto sentido «más pequeños»; siempre se pueden encontrar funciones (¡infinitamente muchas!) que están en C but pero no c 1 1. Estos «espacios de continuidad» por lo tanto forman una secuencia de subconjuntos anidados, como se muestra a continuación.

Cerca de la parte inferior de esta secuencia infinita de conjuntos de funciones nos encontramos con el conjunto
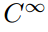
que es, por supuesto, el conjunto de todas las funciones que tiene infinidad de continuo derivados. Muchas funciones conocidas y amigables están en esta última clase(por ejemplo, sin(x); cos (x); e all; todos los polinomios)., Estas funciones se llaman «suave» o «bien comportado» porque uno puede realizar la operación de diferenciación en ellos tantas veces como uno quiera sin cuidado. Pero si bien este conjunto ciertamente tiene infinitos miembros, son raros en el sentido de que la mayoría de las funciones no se comportan tan bien.
el conjunto que es adecuado para la definición de distribuciones es incluso menor
que este. Requiere un criterio adicional: que las funciones tengan un soporte compacto. Este término técnico significa simplemente que una función tiene valores distintos de cero dentro de un dominio finito, y es uniformemente cero fuera de esto., Por lo tanto, el uso de la notación
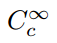
para denotar el conjunto de infinitamente continuamente diferenciable con funciones de soporte compacto, y llamar a esas funciones las funciones de prueba. Para definir una clase de funcionales usando este conjunto como un dominio, debemos estar seguros de que realmente hay miembros de este conjunto., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

La definición
desde este punto, la definición de una distribución es sencilla. Una distribución es un funcional lineal
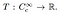
Que es, es una asignación de un conjunto de funciones de prueba a un número real. Analogous to how a specific function acts on an input number and produces an output, specific distributions are defined by how they transform test functions into numbers., La distribución que actúa de la función de prueba φ Se puede escribir como t (φ), o comúnmente como〈T, φ φ.
Ahora se puede ver por qué las distribuciones se llaman funciones generalizadas. Para cualquier
clásica función para la cual la integral

es bien definido, con la correspondiente distribución de F, tal que 〈F,f〉da el valor de esta integral., Sin embargo, también hay distribuciones que no se corresponden con las funciones clásicas; las distribuciones son más generales. Como debería quedar claro a estas alturas, el ejemplo canónico de una distribución que no corresponde a una función clásica es el δ de Dirac., Por lo tanto, finalmente, llegar a una plena definición rigurosa de δ como la distribución tal que

La Generalizada o «Débil» Derivado
La δ distribución es sólo uno de un número infinito de distribuciones que no
corresponden a las funciones clásicas. Podemos obtener algunos más de éstos diferenciando δ en el sentido de distribuciones., Pero, ¿cómo el concepto de una distribución
resuelve el problema de la diferenciación como se discutió anteriormente? Solo necesitamos generalizar el concepto de diferenciación para aplicarlo a las distribuciones.
considere una función f ∈ C1, de modo que sea continuamente diferenciable. Calcular usando integración por partes, vemos que

El término entre corchetes se desvanece desde φ, como una función de prueba, tiene soporte compacto., Esto se generaliza a una distribución, decir que F’, correspondiente a la función f’:

Este cálculo se generaliza fácilmente a las distribuciones que no corresponden a un clásico de la función f., De esta manera, podemos definir la derivada en T de T en el sentido de distribuciones:

Esto también se refiere a veces como la débil derivados, ya que se extiende derivados de las funciones que normalmente no sería diferenciable. Esto generaliza aún más, a derivados de orden superior., Podemos definir la n-ésima derivada de una distribución T como T⁽ü⁾, donde el último es el de la distribución tal que

Aquí,
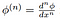
es la clásica de la derivada de la función de prueba, lo que es seguro
a existir por la propia definición de las funciones de prueba!, Se deduce que todas las distribuciones son infinitamente diferenciables (en el sentido de distribuciones).
esto elimina por completo la lucha que Dirac y otros enfrentaron al diferenciar la función δ. Por lo que hemos definido aquí, una derivada de δ simplemente tamiza para el valor de otra derivada de funciones a cero., Formalmente,

Esto proporciona un marco matemático riguroso de los derivados de la δ que apareció en la literatura mucho antes de que esta teoría vino a la existencia.
hay una serie de otras operaciones que se aplican a las funciones que se han generalizado para aplicar a las distribuciones. Pueden ser sumadas y restadas, convolvidas y transformadas usando transformadas de Laplace y Fourier., Sin embargo, es imposible definir la multiplicación de distribuciones de una manera que preserve el álgebra que se aplica a las funciones clásicas (el Teorema de imposibilidad de Schwartz).