Cuando una fracción «normal» contiene fracciones en el numerador o denominador o en ambos, entonces consideramos que es una fracción compleja. Este tipo de fracción también se conoce como fracción compuesta.
Hay dos métodos utilizados para simplificar este tipo de fracción.
Método 1
pasos clave:
- Crear una sola fracción en el numerador y denominador.,
- Aplicar la regla de división de fracciones multiplicando el numerador por el recíproco o inverso del denominador.
- Simplify, if necessary.
el Método 2
los pasos Clave:
- Encontrar el Mínimo Común Denominador (mcd) de todos los denominadores de las fracciones complejas.
- multiplique esta LCD al numerador y denominador de la fracción compleja.
- Simplificar, si es necesario.,
después de repasar algunos ejemplos, debe darse cuenta de que el método 2 es mucho mejor que el método 1 porque casi siempre se necesitan menos pasos para llegar a la respuesta final.
Ejemplos de Cómo Simplificar Fracciones Complejas
Ejemplo 1: Simplifica la fracción compleja a continuación.
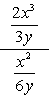
- se utiliza el Método 1
Tanto el numerador y el denominador de la fracción compleja ya están expresadas como fracciones individuales. Esto es genial!,

El siguiente paso será aplicar la división de la regla de multiplicar el numerador por el recíproco del denominador. Termina cancelando los factores comunes para obtener la respuesta final.
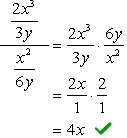
- Usando el método 2
encuentre la LCD de todo el problema, es decir, la LCD de los denominadores superior e inferior.,

Desde la pantalla LCD de 3 y 6y es solo \textbf{6y}, ahora vamos a multiplicar el complejo numerador y el denominador por este LCD. Después de hacerlo, podemos esperar que el problema se reduzca a una sola fracción que se puede simplificar como de costumbre.
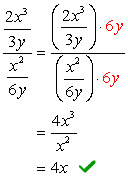
Ejemplo 2: Simplifica la fracción compleja a continuación.,
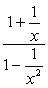
- se utiliza el Método 1
En este método, queremos crear una sola fracción, tanto en el numerador como en el denominador. Obviamente, este problema requeriría que lo hagamos primero antes de realizar la división.
suma las fracciones en el numerador y resta las del denominador.,
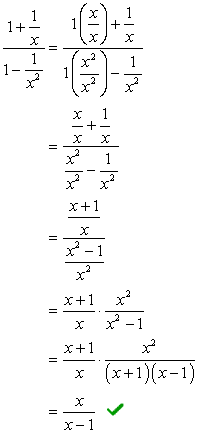
- Usando el método 2
mirando los denominadores \large{x} y \large{x^2}, Su LCD debe ser \large{X^2} multiplique la parte superior e inferior por esta pantalla LCD.
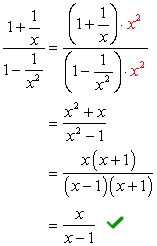
Ejemplo 3: Simplifica la fracción compleja a continuación.,
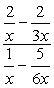
- Usando el método 1
cree fracciones individuales tanto en el numerador como en el denominador, luego siga dividiendo las fracciones.
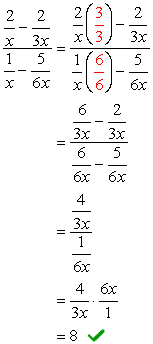
- Usando el método 2
La LCD general de los denominadores es \color{red}6x. Use esto para multiplicar a través de las expresiones superior e inferior.,
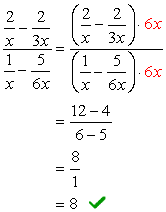
Ejemplo 4: Simplifica la fracción compleja a continuación.
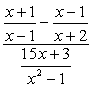
Para este problema, vamos a utilizar el Método 1 sólo.
el problema requiere aplicar el método FOIL (multiplicación de dos binomios) y una factorización simple del trinomio. Puede parecer un poco intimidante al principio; sin embargo, si prestas atención a los detalles, te garantizo que no es tan malo.,
si se observa, el denominador complejo ya está en la forma que queremos-tener un símbolo fraccionario. Esto significa que tenemos que trabajar un poco en el numerador complejo. Nuestro siguiente paso sería transformar el numerador complejo en una fracción «simple» o simple.
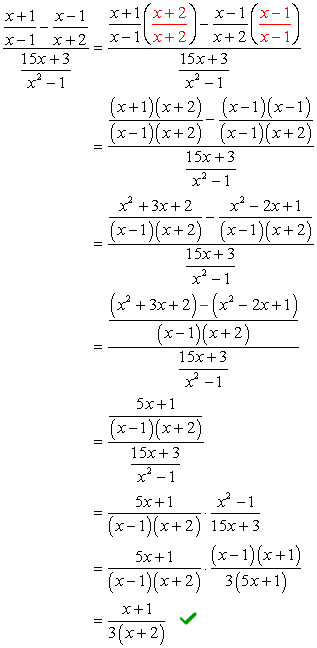
Ejemplo 5: Simplifica la fracción compleja a continuación.
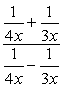
Para este problema, vamos a utilizar el Método 2.,
Observe que la LCD de todos los denominadores es simplemente \color{red} 12x. Use esto como el Multiplicador común para las expresiones superior e inferior.
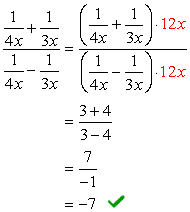
Práctica con Hojas de cálculo
Usted también puede estar interesado en:
la Multiplicación de Fracciones Complejas
División de Números Complejos