Tässä osiossa tarkastellaan Binomisen Lause ja Pascaleina Kolmio.
Pascalin Kolmio
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Sinun pitäisi huomata, että kertoimet (luvut ennen) a ja b ovat:
1 1
1 2 1
1 3 3 1
Jos olet edelleen laajentaa suluissa korkeampien voimien, voit huomata, että sarja jatkuu:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
jne
Tämä sekvenssi tunnetaan Pascalin kolmio., Jokainen numero löytyy lisäämällä yhteen kaksi numeroa suoraan sen yläpuolella.
joten viimeisen rivin 20 löytyy laskemalla yhteen 10 ja 10. Jokainen 10s rivi edellä löytyy lisäämällä yhteen 6 ja 4.
joten on mahdollista laajentaa (a + b) mihin tahansa kokonaislukutehoon tuntemalla Pascal”s-kolmio.
Esimerkki
Etsi (3 + x)3
voima, joka meidän on laajeneva kiinnike on 3, joten katsomme kolmas rivi Pascalin kolmio, joka on 1 3 3 1.,
Joten vastaus on: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(emme korvaa 3-ja b-x laajentamiseen (a + b)3. edellä)
Yleisesti
– Se on, tietenkin, usein epäkäytännöllinen kirjoittaa Pascal”s kolmio joka kerta, kun kaikki, että meidän täytyy tietää ovat merkinnät nnen rivin. Nth-linjan ensimmäinen numero on selvästi 1. Toinen luku on n. Kolmas numero on:
n(n – 1) .
1 × 2
yleensä Nth-linjan RTH-Numero on:
n! (joka on NCR laskin)
r! (n – r)!
missä n!, tarkoittaa ’n kertoma’ ja on yhtä kuin n × (n-1) × … × 2 × 1
nCr on myös usein kirjoitettu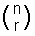 
ja lausutaan ”n valita t”.
Binomisen Lause
Binomisen Lause todetaan, että, jossa n on positiivinen kokonaisluku:
-
(a + b)n = an + (nC1)an-1 b + (nC2)an-2b2 + … + (nCn-1)abn-1 + bn
Esimerkki
Laajenna (4 + 2x)6 nousevassa valtuuksia x-jopa termi x3
Tämä tarkoittaa, käyttää Binomisen lause laajentaa termit sulkeissa, mutta vain mennä niin korkea kuin x3.,
Jotta löytää vastauksen me korvata 4 a Binomisen lause ja 2x b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Binomisen Lause (1 + x)n
edellinen versio binomisen lause toimii vain, kun n on positiivinen kokonaisluku., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
TARJOAMALLA |x| < 1
Huomaa, että kun edellisen sarjan lakkaa, tämä jatkuu ikuisesti.
Esimerkki
Etsi laajentamista (5x + 2)1/2
– Meidän täytyy muuttaa tämän, jotta se näyttää siltä, että (1 + x)1/2, joten voit ottaa pois kertoimella 2:
(5x + 2)1/2 = (2)1/2
Nyt, jos meillä on ” x ” edellä olevassa kaavassa, tarvitsemme 5x/2, jossa meillä on n, tarvitsemme½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Muista, että tämä on voimassa vain, jos -1 < 5x/2 < 1, toisin sanoen, -2/5 < x < 2/5
Käyttämällä Osittainen Jakeet
Voimme laajentaa enemmän monimutkaisia ilmaisuja, nyt, käyttäen menetelmää osittainen jakeet tarvittaessa.
Esimerkki