Distributions
le problème central au cœur des problèmes avec le delta de Dirac et les objets mathématiques similaires
est le problème de la différentiabilité. Comme Dirac l’a déclaré dans la citation ci-dessus, vous ne rencontrez pas vraiment de problèmes si vous utilisez sa fonction δ comme règle symbolique pour la façon dont elle agit sur d’autres fonctions; cependant, il procède à différencier δ dans ses calculs, et c’est là que les problèmes commencent vraiment., Comment savoir a priori « quand ces opérations sont permises » quand on n’a même pas une définition ferme des objets, ou ce que cela signifierait de les différencier? Nous verrons comment ces questions conduisent à la dérivation d’objets mathématiques nouveaux et rigoureusement définis.
Functionals
Considérez comment on détermine normalement la dérivée (ou antidérivative) d’une fonction. Dans des circonstances normales, avec des fonctions « classiques », vous avez une règle bien définie qui décrit comment une fonction mappe un ensemble de nombres réels à un autre ensemble, disons f : ℝ →ℝ., Compte tenu de cela et des définitions de l’intégrale ou de la dérivée, on peut alors étudier clairement les valeurs que ces opérateurs donnent lorsqu’ils sont appliqués à la fonction. Dans le cas de δ, Nous n’avons pas de définition réalisable pour procéder dans ce sens. Au lieu de cela, dans la pratique, δ est principalement défini par la façon dont il fonctionne sur d’autres fonctions bien définies (comme dans (3)). C’est l’idée clé qui mène à la théorie moderne de distributions. Il s’avère que la bonne façon de traiter mathématiquement δ, et une grande classe d’objets similaires, est d’arrêter d’essayer de les Définir comme des fonctions., Cette ligne de pensée est bien décrite par Jean Dieudonné dans sa revue de (voir):
… on commence par une famille de fonctions très « régulières” (généralement avec
respect des propriétés différentielles), qui satisfont certaines relations (généralement
intégrales), ou sur lesquelles certaines opérations sont possibles; et
alors on découvre qu’une famille a priori plus grande de fonctions satisfait
les mêmes relations, ou peut être soumise à des opérations similaires. Beaucoup de
questions peuvent alors naturellement être posées: cette nouvelle famille est-elle vraiment
différente de la première?, Si c’est le cas, quelles sont les relations entre les deux familles, et peut-on donner une description précise de la nouvelle?
Ce n’est que dans la dernière étape de la « préhistoire” qu’émergera ce que l’on peut appeler un point de vue révolutionnaire, avec l’idée que
la « nouvelle famille” pourrait être constituée d’objets autres que des fonctions.
les autres objets auxquels il est fait allusion sont des objets fonctionnels. Vous pouvez penser à un
fonctionnel comme une fonction de fonctions., Comme une fonction est un mappage unique d’un ensemble de nombres
à un autre, une fonction F peut être définie comme un mappage F : C →ℝ,
où C est un ensemble de fonctions. Autrement dit, une fonction de cartes fonctionnelles à des nombres réels
., Un exemple simple d’une fonctionnelle de ce type est l’intégrale:

ce qui est clairement une fonction f d’un ensemble de convenablement intégrable fonctions et des cartes pour un nombre réel, la valeur de l’intégrale, ou l’aire sous la courbe de f(x) entre a et b. C’est juste un exemple unique., On peut imaginer un nombre infini de fonctionnels, et des ensembles de fonctionnels; on pourrait même continuer à généraliser et définir des mappages d’ensembles de fonctionnels à des nombres réels. Qui n’est ni ici ni là-bas. Ce qui est important, c’est que le concept fonctionnel puisse être utilisé pour définir des distributions.
L’Ensemble des Fonctions de Test
Nous avons besoin d’une définition plus pour atteindre notre objectif. Cela revient à spécifier L’ensemble C de fonctions à partir duquel les distributions mapperont les fonctions à des nombres réels., Les fonctions sont souvent rassemblées dans des ensembles qui spécifient leur degré de continuité, de différentiabilité et la continuité de leurs dérivées. On dit qu’une fonction f est dans L’ensemble c ∈ (écrire f ∈ C C) si elle est continue sur toute la ligne réelle dans le sens où la limite en tous points est la même lorsqu’elle est prise à gauche ou à droite; elle n’est pas nécessairement différentiable. On dit que f ∈ C1 si sa dérivée existe et est continue, c’est-à-dire f ’ ∈ C⁰. Par exemple, la fonction g(x) = |x| est continue mais non différentiable à x= 0; g est en C⁰ mais pas en C1., Nous pouvons généraliser cela et dire que Cⁿ est l’ensemble des fonctions qui ont pour les fonctions continues leurs N premières dérivées, où n est un entier.
à mesure que n devient plus grand, les ensembles deviennent dans un sens « plus petits”; vous pouvez toujours trouver des fonctions (infiniment nombreuses!) qui sont en C but mais pas en C 1 1. Ces” espaces de continuité » forment donc une séquence de sous-ensembles imbriqués, comme illustré ci-dessous.

Près de la partie inférieure de cette séquence infinie d’ensembles de fonctions, nous trouvons le set
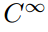
ce qui est bien sûr l’ensemble de toutes les fonctions qui ont une infinité continue de produits dérivés. De nombreuses fonctions bien connues et conviviales sont dans cette dernière classe(par exemple sin(x); cos (x); eˣ; tous les polynômes)., Ces fonctions sont appelées « lisses” ou » bien comportées » car on peut effectuer l’opération de différenciation sur elles autant de fois qu’on le souhaite sans soin. Mais alors que cet ensemble a certainement infiniment de membres, ils sont rares dans le sens où la plupart des fonctions ne sont pas si bien comportées.
l’ensemble qui convient à la définition des distributions est encore plus petit
que celui-ci. Cela nécessite un critère supplémentaire: que les fonctions aient un support compact. Ce terme technique signifie simplement qu’une fonction a des valeurs non nulles dans un domaine fini, et est uniformément nulle en dehors de cela., Par conséquent, nous utilisons la notation
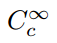
pour décrire l’ensemble de l’infiniment dérivable en permanence des fonctions à support compact, et d’appeler ces fonctions de fonctions de test. Afin de définir une classe de fonctionnels utilisant cet ensemble comme domaine, nous devons être sûrs qu’il existe réellement des membres de cet ensemble., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Définition
à Partir de ce stade, la définition d’une distribution est simple. Une distribution est une fonctionnelle linéaire
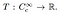
C’est, c’est une cartographie de l’ensemble des fonctions de test d’un nombre réel. De manière analogue à la façon dont une fonction spécifique agit sur un nombre d’entrée et produit une sortie, les distributions spécifiques sont définies par la façon dont elles transforment les fonctions de test en nombres., La distribution agissant de la fonction d’essai φ Peut être écrite comme T (φ), ou généralement comme〈T, φ〉.
on peut maintenant voir pourquoi les distributions sont appelées fonctions généralisées. Pour tout
classique de la fonction pour laquelle l’intégrale

est bien défini, il y a une distribution correspondante de F tels que 〈F,φ〉donne la valeur de cette intégrale., Cependant, il existe également des distributions qui ne correspondent pas aux fonctions classiques; les distributions sont plus générales. Comme il devrait être clair maintenant, L’exemple canonique d’une distribution qui ne correspond pas à une fonction classique est le Dirac δ., Nous avons donc enfin arriver à une entièrement définition rigoureuse de δ comme la distribution de tels que:

L’Généralisée ou « Faible”, Dérivé
Le δ distribution est un seul d’une infinité de distributions qui ne sont pas
correspondent à des fonctions classiques. Nous pouvons en obtenir d’autres en différenciant δ au sens de distributions., Mais comment le concept d’une distribution
résout – il le problème de la différenciation comme discuté précédemment? Il suffit de généraliser le concept de différenciation pour l’appliquer aux distributions.
considérons une fonction f ∈ C1, de sorte qu’elle soit continuellement différentiable. Le calcul en utilisant l’intégration par parties, nous voyons que

Le terme entre crochets disparaît puisque φ, comme une fonction de test, a support compact., Cette généralise à une distribution, dire F’, correspondant à la fonction f’:

Ce calcul se généralise assez facilement aux distributions qui ne correspondent pas à un classique de la fonction f., De cette façon, on peut définir la dérivée de T’ de T dans le sens des distributions:

C’est aussi parfois appelée la faiblesse des dérivés, puisqu’il s’étend à des instruments dérivés pour des fonctions qui ne seraient normalement pas dérivable. Cela se généralise encore plus loin, aux dérivés d’ordre supérieur., On peut définir la dérivée nième d’une distribution T de T⁽ü⁾, lorsque celle-ci est la distribution de tels que:

Ici,
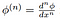
est le classique de la dérivée de la fonction de test, qui est assurée d’
pour exister de par la définition de fonctions de test!, Il s’ensuit que toutes les distributions sont infiniment différentiables (au sens de distributions).
cela supprime entièrement la lutte à laquelle Dirac et d’autres ont fait face lors de la différenciation de la fonction δ. Par ce que nous avons défini ici, une dérivée de δ Tamise simplement la valeur d’une autre dérivée de fonctions à zéro., Si vous avez besoin d’un système de partage de données, vous pouvez utiliser le système de partage de données de type »div »(« div »en anglais), qui est un système de partage de données de type »div »(« div »en anglais), qui est un système de partage de données de type » div » (« div » en anglais). ce86685ba0 » >
ceci fournit un cadre mathématique rigoureux pour les dérivées de δ qui sont apparues dans la littérature bien avant que cette théorie n’ait vu le jour.
Il existe un certain nombre d’autres opérations qui s’appliquent aux fonctions qui ont été généralisées pour s’appliquer aux distributions. Ils peuvent être ajoutés et soustraits, convolus et transformés à l’aide de transformées de Laplace et de Fourier., Cependant, il est impossible de définir la multiplication des distributions d’une manière qui préserve l’algèbre qui s’applique aux fonctions classiques (le théorème D’impossibilité de Schwartz).