Icosaèdre

L’icosaèdre régulier est l’un des cinq solides Platoniciens. C’est un polyèdre régulier convexe composé de vingt faces triangulaires, avec cinq se rencontrant à chacun des douze sommets. Il a 30 arêtes et 12 sommets. Son double polyèdre est le dodécaèdre.,

Dimensions

Si la longueur de l’arête d’un icosaèdre régulier est , le rayon d’une sphère circonscrite (celui qui touche l’icosaèdre à tous les sommets) est

et le rayon d’un inscrit sphère tangente à chacun de l’icosaèdre visages) est

tandis que le midradius, qui touche le milieu de chaque bord, est

où 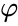(également appelé ) est le nombre d’or.,

Aire et de volume

La surface et le volume d’un icosaèdre régulier d’arête de longueur sont:

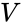
coordonnées Cartésiennes

Les coordonnées Cartésiennes de définir les sommets de l’icosaèdre avec bord-longueur 2, centré à l’origine:

où est le nombre d’or (aussi écrit τ)., Notez que ces sommets forment cinq ensembles de trois rectangles dorés mutuellement centrés et mutuellement orthogonaux.

Les 12 arêtes d’un octaèdre régulier peuvent être partitionnées dans le nombre d’or de sorte que les sommets résultants définissent un icosaèdre régulier. Ceci est fait en plaçant d’abord des vecteurs le long des bords de l’octaèdre de sorte que chaque face soit délimitée par un cycle, puis en partitionnant de manière similaire chaque bord dans la moyenne d’or le long de la direction de son vecteur., Les cinq octaèdres définissant un icosaèdre donné forment un composé polyédrique régulier, tout comme les deux icosaèdres qui peuvent être définis de cette manière à partir d’un octaèdre donné.

Construction par un système de lignes équiangulaires

la construction suivante de l’icoshaedron évite les calculs fastidieux dans le champ des nombres nécessaires dans les approches plus élémentaires.

L’Existence de l’icosaèdre équivaut à l’existence de six lignes équiangulaires dans., En effet, l’intersection d’un tel système de droites équiangulaires avec une sphère euclidienne centrée à leur intersection commune donne les douze sommets d’un icosaèdre régulier que l’on peut facilement vérifier. Inversement, en supposant l’existence d’un icosaèdre régulier, les droites définies par ses six paires de sommets opposés forment un système équiangulaire.

pour construire un tel système équiangulaire, on commence par la matrice

de taille carrée., (Mnémonique :la matrice code les angles, aigus pour une entrée positive, obtus sinon, entre cinq sommets cycliquement consécutifs adjacents à un premier sommet d’un icosaèdre centré à l’origine.)

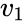
un calcul simple donne . Cela implique que a des valeurs propres , les deux avec une multiplicité 3 puisque est symétrique et de trace 0., La matrice induit thusan structure Euclidienne sur le quotient de l’espace qui est isomorphe a ‘ depuis le noyau de dimension 3. L’image sous la projection des six axes de coordonnées dans forme ainsi un système de six lignes équiangulaires dans se coupant par paire à un angle aigu commun de ., La projection orthogonale de dans le -sous-espace propre de rendements ainsi, les douze sommets de l’icosaèdre.

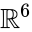
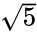
Une deuxième construction simple de l’icosaèdre utilise la théorie des représentations du groupe alternatif agissant par isométries directes sur l’icosaèdre.

Stellations

selon les règles spécifiques définies dans le livre les cinquante-neuf icosaèdres, 59 stellations ont été identifiées pour l’icosaèdre régulier. La première forme est l’icosaèdre lui-même., L’un est un solide Kepler-Poinsot régulier. Trois sont des polyèdres composés réguliers.

21 de 59 stellations

Les faces de l’icosaèdre prolongée vers l’extérieur comme les avions se croisent, la définition des régions dans l’espace comme le montre ce stellation diagramme des intersections dans un seul plan.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Ceux-ci sont invariants sous les mêmes rotations que le tétraèdre, et sont quelque peu analogues au cube snub et au dodécaèdre snub, y compris certaines formes chirales et certaines avec une symétrie Th, c’est-à-dire ont des plans de symétrie différents du tétraèdre. L’icosaèdre a un grand nombre de stellations, y compris l’un des polyèdres de Kepler-Poinsot et certains des composés réguliers, qui pourraient être discutés ici.

l’icosaèdre est unique parmi les solides platoniciens en possédant un angle dièdre d’au moins 120°. Son angle dièdre est d’environ 138.19°.,les icosaèdres ne peuvent pas être utilisés comme cellules d’un polychoron régulier convexe car une telle construction ne répondrait pas à l’exigence qu’au moins trois faces se rencontrent au niveau d’un sommet et laissent un défaut positif de pliage en trois dimensions, les icosaèdres ne peuvent pas être utilisés comme cellules d’un polychoron régulier convexe car, de même, au moins trois cellules doivent se rencontrer au niveau d’un bord et laisser un défaut positif de pliage en quatre dimensions (en général pour un polytope convexe en dimensions, au moins trois facettes doivent se rencontrer à un pic et laisser un défaut positif pour le pliage dans l’espace n)., Cependant, lorsqu’ils sont combinés avec des cellules appropriées ayant des angles dièdres plus petits, les icosaèdres peuvent être utilisés comme cellules dans les polychores semi-réguliers (par exemple la cellule snub 24), tout comme les hexagones peuvent être utilisés comme faces dans les polyèdres semi-réguliers (par exemple l’icosaèdre tronqué). Enfin, les polytopes non convexes n’ont pas les mêmes exigences strictes que les polytopes convexes, et les icosaèdres sont en effet les cellules de la cellule icosaédrique 120, l’une des dix polychores réguliers non convexes.

un icosaèdre peut aussi être appelé bipyramide Pentagonal gyroélongé., Il peut être décomposé en une pyramide pentagonale gyroélongée et une pyramide pentagonale ou en un antiprisme pentagonal et deux pyramides pentagonales égales.

L’icosaèdre peut aussi être appelé un camouflet tétraèdre, comme snubification d’un tétraèdre régulier donne un icosaèdre régulier., Alternativement, en utilisant la nomenclature des polyèdres snub qui se réfère à un cube snub comme un cuboctaèdre snub (cuboctaèdre = cube rectifié) et un dodécaèdre snub comme un icosidodécaèdre snub (icosidodécaèdre = dodécaèdre rectifié), on peut appeler l’icosaèdre l’octaèdre snub (octaèdre = tétraèdre rectifié).

un icosaèdre rectifié forme un icosidodécaèdre.

icosaèdre vs dodécaèdre

lorsqu’un icosaèdre est inscrit dans une sphère, il occupe moins de volume de la sphère (60,54%) qu’un dodécaèdre inscrit dans la même sphère (66,49%).,

de plus, comme ce sont des duals, il est possible de transformer l’un en l’Autre(voir ci-dessous).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	Dans certains jeux de rôle, le dé à vingt faces (en abrégé, d20) est utilisé pour déterminer le succès ou l’échec d’une action. Ce dé est sous la forme d’un icosaèdre régulier. Il peut être numéroté de » 0 « à » 9 « deux fois (sous quelle forme il sert généralement de dé à dix faces, ou d10), mais la plupart des versions modernes sont étiquetées de » 1 « à »20 ». Voir système d20.,

Un icosaèdre est les trois dimensions de la planche de jeu pour Icosagame, anciennement connu comme le Ico Crystal Jeu.

Un icosaèdre est utilisé dans le jeu de plateau Scattergories choisir une lettre de l’alphabet. Six lettres peu utilisées, telles que X, Q et Z, sont omises.

à l’intérieur d’un Magic 8-Ball, diverses réponses aux questions oui-non sont imprimées sur un icosaèdre régulier.

l’icosaèdre affiché sous une forme fonctionnelle est visible dans la teinte claire Sol De La Flor., La rosette formée par les pièces qui se chevauchent montre une ressemblance avec la fleur de frangipanier.

Si chaque arête d’un icosaèdre est remplacée par une résistance d’un ohm, la résistance entre les sommets opposés est de 0,5 ohms, et celle entre les sommets adjacents de 11/30 ohms.

le groupe de symétrie de l’icosaèdre est isomorphe au groupe alternatif sur cinq lettres. Ce groupe simple non-abélien est le seul sous-groupe normal non trivial du groupe symétrique sur cinq lettres., Étant donné que le groupe de Galois de l’équation quintique générale est isomorphe au groupe symétrique sur cinq lettres, et le fait que le groupe icosaédrique est simple et non abélien signifie que les équations quintiques n’ont pas besoin d’avoir une solution en radicaux. La preuve du théorème D’Abel-Ruffini utilise ce simple fait, et Felix Klein a écrit un livre qui a fait usage de la théorie des symétries icosaédriques pour dériver une solution analytique à l’équation quintique générale.,

Voir aussi

Modèle:Wiktionarypar

• l’icosaèdre Tronqué
• polyèdre Régulier
• Géodésique grilles d’utiliser d’une manière itérative traversé l’icosaèdre pour générer des grilles sur une sphère
• Jessen de l’icosaèdre

Modèle:Wikisource1911Enc

Modèle:Commonscat

• Weisstein, Eric W., « l’Icosaèdre » de MathWorld.
• des maquettes en Papier de l’icosaèdre
• L’Uniforme Polyèdres
• K. J. M., MacLean, une analyse géométrique des cinq solides platoniciens et D’autres Polyèdres Semi-réguliers
• modèle icosaèdre interactif – fonctionne directement dans votre navigateur Web
• polyèdres de Réalité Virtuelle L’Encyclopédie des polyèdres
• Tulane.,edu est Une discussion de la super structure et l’icosaèdre
• des maquettes en Papier de Polyèdres de Nombreux liens
• Origami de Polyèdres Modèles est faite avec un Modulaire Origami
• la vidéo de la icosaédrique miroir est une sculpture

Modèle:Polyèdres

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri je rregulltsr:Икосаедарsv:Ikosaederta:a éclaté முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.