Introduction à la Philosophie: Logique

Il existe une vision ancienne, encore largement répandue, selon laquelle ce qui rend les êtres humains Spéciaux—ce qui nous distingue des « bêtes du champ”—est que nous sommes rationnels. En quoi consiste la rationalité? C’est une question vexée, mais une réponse possible va à peu près comme ceci: nous manifestons notre rationalité en nous engageant dans des activités qui impliquent un raisonnement—faire des revendications et les soutenir avec des raisons, agir en accord avec des raisons et des croyances, tirer des conclusions à partir de preuves disponibles, etc.,

cette activité de raisonnement peut être bien faite et elle peut être mal faite; elle peut être faite correctement ou incorrectement. La logique est la discipline qui vise à distinguer le bon raisonnement du mauvais.

Bon raisonnement n’est pas nécessairement efficace raisonnement. En fait, comme nous le verrons dans un chapitre ultérieur sur les erreurs logiques, le mauvais raisonnement est omniprésent et souvent extrêmement efficace—dans le sens où les gens en sont souvent persuadés. En logique, la norme de bonté n’est pas l’efficacité dans le sens de la persuasion, mais plutôt l’exactitude selon des règles logiques.,

par exemple, considérez Hitler. Il persuada toute une nation d’accepter une variété de propositions qui étaient non seulement fausses, mais carrément mauvaises. Vous ne serez pas surpris d’entendre que si vous l’examinez de manière critique, son raisonnement ne passe pas le rassemblement logique. Les arguments de Hitler étaient efficaces, mais pas logiquement corrects. De plus, ses techniques de persuasion vont au-delà du raisonnement dans le sens de soutenir les revendications avec des raisons. Hitler s’est appuyé sur des menaces, des manipulations émotionnelles, des affirmations non étayées, etc. Il existe de nombreuses astuces rhétoriques que l’on peut utiliser pour persuader.,

en logique, nous étudions les règles et les techniques qui nous permettent de distinguer le bon raisonnement correct du mauvais raisonnement incorrect.

étant donné qu’il existe une variété de types de raisonnement et de méthodes différents pour évaluer chacun de ces types, ainsi que diverses opinions divergentes sur ce qui constitue un raisonnement correct, il existe de nombreuses approches de l’entreprise logique. On parle de logique, mais aussi de logique. Une logique n’est qu’un ensemble de règles et de techniques permettant de distinguer le bon raisonnement du mauvais., Une logique doit formuler des normes précises pour évaluer le raisonnement et développer des méthodes pour appliquer ces normes à des cas particuliers.

Notions de base

Le Raisonnement implique des affirmations ou des déclarations—les faire et les étayer avec des raisons, en tirant leurs conséquences. Les Propositions sont les choses que nous revendiquons, énonçons, affirmons.

Les Propositions sont le genre de choses qui peuvent être vraies ou fausses. Ils sont exprimés par des phrases déclaratives., Nous utilisons de telles phrases pour faire toutes sortes d’affirmations, des faits de routine (« la Terre tourne autour du Soleil”), aux grandes thèses métaphysiques (« la réalité est un absolu immuable, sans traits, unifié”), aux revendications sur la moralité (« il est faux de manger de la viande”).

Il est important de distinguer les phrases dans l’Humeur déclarative, qui expriment des propositions, des phrases dans d’autres humeurs, qui ne le font pas. Les phrases interrogatives, par exemple, posent des questions (« pleut-il?”), et des phrases impératives émettent des commandes (« ne buvez pas de kérosène.”)., Cela n’a aucun sens de se demander si ce genre de phrases exprime des vérités ou des mensonges, de sorte qu’elles n’expriment pas de propositions.

nous distinguons également les propositions des phrases qui les expriment, car une seule proposition peut être exprimée par des phrases différentes. « Il pleut” et « il pleut” les deux expriment l’idée qu’il pleut; une phrase en anglais, l’autre en allemand. En outre, « Jean aime Marie” et » Marie est aimée par Jean  » expriment tous deux la même proposition.

L’unité fondamentale de raisonnement est l’argument., En logique, par” argument », nous ne voulons pas dire un désaccord, une correspondance criante; nous définissons plutôt le terme avec précision:

Argument = un ensemble de propositions, dont l’une, la conclusion, est (censée être) soutenue par les autres, les prémisses.

Si nous raisonnons en faisant des revendications et en les sauvegardant avec des raisons, alors la revendication qui est sauvegardée est la conclusion d’un argument; les raisons données pour le soutenir sont les prémisses de l’argument., Si nous raisonnons en tirant une inférence à partir d’un ensemble d’énoncés, alors l’inférence que nous tirons est la conclusion d’un argument, et les énoncés dont il est tiré sont les prémisses.

Nous incluons la haie entre parenthèses— »supposée être”—dans la définition pour faire de la place aux mauvais arguments. Un mauvais argument, très Grosso Modo, est celui où les prémisses ne soutiennent pas la conclusion; les prémisses d’un bon argument soutiennent en fait la conclusion.

analyse des Arguments

le passage suivant exprime un argument:

ce passage:

encore une fois, le but ultime de la logique est d’évaluer les arguments—de distinguer le bon du mauvais. Pour ce faire, il faut des distinctions, des définitions, des principes et des techniques qui seront décrits dans les chapitres suivants. Pour l’instant, nous allons nous concentrer sur l’identification et la reconstruction d’arguments.

la première tâche consiste à expliquer les arguments—à énoncer explicitement leurs prémisses et leurs conclusions., Une façon perspicace de le faire est simplement d’énumérer les phrases déclaratives exprimant les propositions pertinentes, avec une ligne séparant les prémisses de la conclusion, ainsi:

1. Mcdonald’s paie ses travailleurs très bas salaires.
2. Les animaux qui fournissent la viande de Mcdonald’s sont élevés dans des conditions déplorables.
3. La nourriture de Mcdonald’s est très malsaine.
4. / \par conséquent, vous ne devriez pas manger chez Mcdonald’s.

ceci est une explication du premier passage argumentatif ci-dessus., Pour identifier la conclusion d’un argument, il est utile de se demander: « Qu’est-ce que cette personne essaie de me convaincre de croire en disant ces choses? Quel est le point final de ce passage?” La réponse est assez claire dans ce cas. Un autre indice quant à ce qui se passe dans le passage est fourni par le mot « parce que” dans la troisième phrase. Avec d’autres mots, comme « depuis” et « pour”, il indique la présence d’une prémisse. Nous pouvons appeler de tels mots des marqueurs de prémisse. Le symbole « /∴” peut être lu comme un raccourci pour « donc., »Avec des expressions comme » par conséquent”, « ainsi”, « il s’ensuit que” et « ce qui implique que” » par conséquent  » est un indicateur que la conclusion de l’argument est sur le point de suivre. Nous appelons ces locutions des marqueurs de conclusion. Un tel marqueur n’est pas présent dans le premier argument, mais nous en voyons un dans le second, qui peut être expliqué ainsi:

1. l’univers est vaste et complexe.
2. L’univers affiche un degré d’ordre étonnant.
3. Les planètes orbitent autour du soleil selon des lois régulières.
4. Les parties les plus minuscules des animaux sont disposées précisément pour servir leurs objectifs.,
5. Un tel ordre et une telle complexité ne peuvent pas survenir au hasard.
6. / \par conséquent, L’univers doit être le produit d’un concepteur d’un pouvoir et d’un intellect énormes: Dieu.

plusieurs points de comparaison avec notre première explication méritent d’être notés ici. Tout d’abord, comme mentionné, nous avons été alertés de la conclusion par le mot « donc. »Deuxièmement, ce passage nécessitait beaucoup plus de paraphrase que le premier. La deuxième phrase est interrogative, Non déclarative, et donc elle n’exprime pas de proposition., Puisque les arguments sont, par définition, des collections de propositions, nous devons nous limiter aux phrases déclaratives lors de leur explication. Puisque la réponse à la question rhétorique de la deuxième phrase est clairement « oui », nous paraphrasons comme indiqué. La troisième phrase exprime deux propositions, donc dans notre explication nous les séparons; chacune est une prémisse.

donc, parfois, lorsque nous expliquons un argument, nous devons prendre ce qui est présent dans le passage argumentatif et le changer légèrement, de sorte que toutes les phrases que nous écrivons expriment les propositions présentes dans l’argument., C’est la paraphrase. À d’autres moments, nous devons faire encore plus. Par exemple, nous pouvons avoir à introduire des propositions qui ne sont pas explicitement mentionnées dans le passage argumentatif, mais qui sont sans aucun doute utilisées dans le raisonnement de l’argument.

Il y a un mot grec pour les passages argumentatifs qui laissent certaines propositions non écrites: enthymèmes. Voici un exemple:

Il y a une prémisse implicite qui se cache en arrière—plan ici-quelque chose qui n’a pas été dit, mais qui doit être vrai pour que l’argument passe. Nous avons besoin d’une affirmation qui relie la prémisse à la conclusion—qui comble le fossé entre eux. Quelque chose comme ça: un Dieu Tout-aimant ne permettrait pas aux innocents de souffrir. Ou peut-être: la souffrance généralisée est incompatible avec l’idée d’une divinité qui aime tout. La prémisse indique la souffrance, tandis que la conclusion concerne Dieu; ces propositions relient ces deux revendications., Une explication complète du passage argumentatif rendrait une proposition comme celle-ci explicite:

1. de nombreuses personnes innocentes partout dans le monde souffrent.
2. Un Dieu Tout-aimant ne permettrait pas aux innocents de souffrir.
3. / \Il ne peut donc pas y avoir de Dieu Tout-aimant.

c’est la marque des types de prémisses tacites que nous voulons découvrir: si elles sont fausses, elles sapent l’argument., Souvent, des prémisses comme celle-ci ne sont pas établies pour une raison: ce sont des revendications controversées par elles-mêmes, nécessitant des preuves à l’appui; donc l’arguant les laisse de côté, préférant ne pas s’enliser. Lorsque nous les dégainons, cependant, nous pouvons forcer un échange dialectique plus robuste, en concentrant l’argument sur le cœur de la question. Dans ce cas, une discussion sur la compatibilité de la bonté et du mal de Dieu dans le monde serait de mise. Il y a beaucoup de choses à dire sur ce sujet., Philosophes et théologiens ont développé des arguments élaborés au cours des siècles pour défendre l’idée que la bonté de Dieu et la souffrance humaine sont en fait compatibles.

jusqu’à présent, notre analyse des arguments n’a pas été particulièrement profonde. Nous avons noté l’importance d’identifier la conclusion et d’énoncer clairement les prémisses, mais nous n’avons pas examiné comment des ensembles de prémisses peuvent étayer leurs conclusions. Nous avons simplement noté que, collectivement, les prémisses appuient les conclusions., Nous n’avons pas regardé comment ils le font, quels types de relations ils ont les uns avec les autres. Cela nécessite une analyse approfondie.

souvent, différentes prémisses soutiendront une conclusion—ou une autre prémisse—individuellement, sans l’aide d’aucun autre. Considérez cet argument simple:

Les Propositions 1 et 2 soutiennent la conclusion, la proposition 3—et elles le font indépendamment. Chacun nous donne une raison de croire que la guerre était injuste, et chacun se tient debout comme une raison, même si nous supposions que l’autre n’était pas vrai; c’est la marque des indépendants locaux.

Il peut être utile, surtout lorsque les arguments sont plus complexes, de dessiner des diagrammes qui décrivent les relations entre les prémisses et la conclusion., Nous pourrions représenter l’argument ci-dessus comme suit:

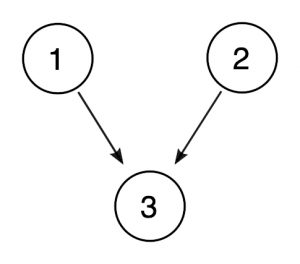
Dans un tel diagramme, les nombres encerclés représentent les propositions et les flèches représentent la relation de support d’une proposition à une autre. Puisque les propositions 1 et 2 supportent chacune 3 indépendamment, elles obtiennent leurs propres flèches.

D’autres relations entre les prémisses sont possibles. Parfois, les prémisses ne soutiennent les conclusions qu’indirectement, en nous donnant une raison de croire à une autre prémisse, qui est intermédiaire entre les deux revendications., Considérez l’argument suivant:

dans cet exemple, la proposition 1 soutient la proposition 2 (le mot « d’où” est un indice), tandis que la proposition 2 soutient directement la conclusion dans 3., Nous décririons les relations entre ces propositions ainsi:

parfois, les prémisses doivent travailler ensemble pour fournir un support à une autre revendication, non pas parce que l’une d’elles fournit une raison de croire l’autre, mais parce qu’aucune d’elles ne fournit le support nécessaire Considérez ce qui suit:

dans cet argument, ni la prémisse 1 ni la prémisse 2 ne soutiennent la conclusion à elles seules; au contraire, la deuxième prémisse, pour ainsi dire, fournit une clé qui déverrouille la conclusion à partir de la prémisse conditionnelle 1. Nous pouvons indiquer une telle interdépendance schématiquement avec des crochets, ainsi:

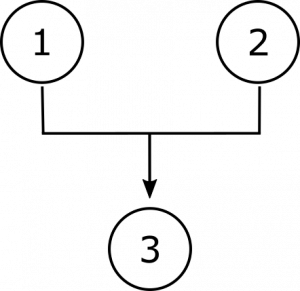
Les arguments de cette manière peuvent être utiles à la fois pour comprendre comment ils fonctionnent et pour informer toute tentative de s’engager de manière critique avec eux., On peut clairement voir dans le premier argument que toute considération avancée contraire à l’une des prémisses indépendantes ne Sapera pas complètement l’appui à la conclusion, car il existe encore une autre prémisse lui fournissant un certain degré d’appui. Dans le deuxième argument, cependant, des raisons contraires à la deuxième prémisse couperaient le support de la conclusion à la racine; et tout ce qui est contraire à la première prémisse laissera la seconde dans le besoin d’appui. Et dans le troisième argument, des considérations contraires à l’une ou l’autre des prémisses communes saperont l’appui à la conclusion., Surtout lorsque les arguments sont plus complexes, ces aides visuelles peuvent nous aider à reconnaître toutes les inférences contenues dans l’argument.

peut-être sera-t-il utile de conclure en considérant un argument un peu plus complexe. Considérons la nature des nombres:

la conclusion de cet argument est la dernière proposition, que les nombres sont des objets abstraits. Notez que la première prémisse nous donne le choix entre cette affirmation et une alternative—qu’ils sont concrets. La deuxième prémisse nie cette alternative, et donc les prémisses 1 et 2 travaillent ensemble pour soutenir la conclusion:

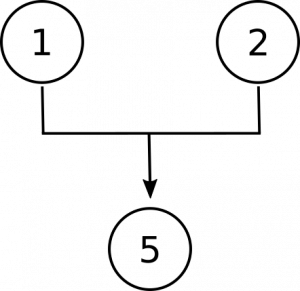
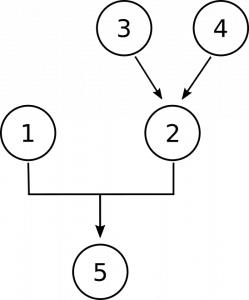
maintenant, nous devons faire de la place dans notre diagramme pour les propositions 3 et 4. Ils sont là pour nous donner des raisons de croire que les chiffres ne sont pas des objets concrets., Premièrement, en affirmant que les nombres ne sont pas situés dans l’espace comme le sont les objets concrets, et deuxièmement en affirmant que les nombres n’interagissent pas avec d’autres objets, comme le font les objets concrets. Ce sont des raisons distinctes et indépendantes de croire qu’elles ne sont pas concrètes, nous nous retrouvons donc avec ce diagramme:

logique et philosophie

Au cœur de l’entreprise logique se trouve une question philosophique: Qu’est-ce qui fait un bon argument? Autrement dit, qu’est-ce qu’un ensemble de revendications pour fournir un soutien à une autre revendication? Ou peut-être: quand sommes-nous justifiés de tirer des inférences?, Pour répondre à ces questions, les logiciens ont développé une grande variété de systèmes logiques, couvrant différents types d’arguments et appliquant différents principes et techniques. De nombreux outils développés dans la logique peuvent être appliqués au-delà des limites de la philosophie. Le mathématicien prouvant un théorème, l’informaticien programmant un ordinateur, le linguiste modélisant la structure du langage—tout cela utilise des méthodes logiques., Parce que la logique a une application aussi large, et en raison de la sophistication formelle/mathématique de nombreux systèmes logiques, elle occupe une place unique dans le programme philosophique. Un cours de logique est généralement différent des autres cours de philosophie en ce sens que très peu de temps est consacré à s’engager directement et à tenter de répondre aux « grandes questions”; au contraire, on se met très rapidement à l’apprentissage des formalismes logiques. Les questions auxquelles la logique tente de répondre sont des questions philosophiques importantes, mais les techniques développées pour y répondre méritent d’être étudiées par elles-mêmes.,

cela ne signifie pas pour autant que nous devrions considérer la logique et la philosophie comme simplement tangentiellement liées; au contraire, elles sont profondément liées. Pour toutes les cloches et de sifflets formels présentés dans le dernier système logique haut de gamme, au fond, il fait partie d’un effort pour répondre à la question fondamentale de ce qui découle de quoi. De plus, la logique est utile au philosophe pratiquant d’au moins trois autres manières.

Les Philosophes tentent de répondre à des questions profondes et vexantes—sur la nature de la réalité, ce qui constitue une bonne vie, comment créer une société juste, etc., Ils donnent leurs réponses à ces questions, et les réponses avec des raisons. Ensuite, d’autres philosophes examinent leurs arguments et répondent par des élaborations et des critiques—arguments qui leur sont propres. La philosophie est conduite et progresse par l’échange d’arguments. Comme ils sont l’outil principal de leur métier, les philosophes savent mieux un petit quelque chose sur ce qui fait de bons arguments! La logique est donc essentielle à la pratique de la philosophie.,

Mais la logique n’est pas seulement un outil d’évaluation des arguments philosophiques; elle a modifié le cours de la conversation philosophique en cours. Au fur et à mesure que les logiciens développaient des systèmes formels pour modéliser la structure d’un éventail toujours plus large de pratiques discursives, les philosophes ont pu appliquer leurs idées directement aux problèmes philosophiques traditionnels et reconnaître des voies de recherche auparavant cachées. Depuis le début du 20ème siècle en particulier, la prolifération de nouvelles approches en logique a déclenché une révolution dans la pratique de la philosophie., Il n’est pas trop exagéré de dire qu’une grande partie de l’histoire de la philosophie au 20e siècle a constitué une tentative continue de s’attaquer aux nouveaux développements de la logique et à l’accent philosophique sur le langage qu’ils semblaient exiger. Aucun sujet philosophique – de la métaphysique à l’éthique en passant par l’épistémologie et au—delà-n’a été épargné par cette révolution.

enfin, la logique elle-même est la source de questions philosophiques fascinantes. La question fondamentale en son cœur—qu’est-ce qu’une revendication doit suivre des autres?,- ramifie dans une myriade de directions, fournissant un terrain fertile pour la spéculation philosophique. Il est logique, et puis il y a la philosophie de la logique. La logique est dite « formelle”, par exemple. Qu’est-ce que ça veut dire? C’est une question étonnamment difficile à répondre. Nos formulations logiques les plus simples de phrases conditionnelles (celles impliquant « si”), conduisent à des paradoxes apparents. Comment faut-il être résolu? Nos formalismes devraient-ils être modifiés pour mieux saisir les significations en langage naturel des conditionnels? Quelle est la relation appropriée entre les systèmes logiques et les langages naturels, de toute façon?,

traditionnellement, la plupart des logiciens ont accepté que la logique devrait être « bivalente »: chaque proposition est vraie ou fausse. Mais les langues naturelles contiennent des termes vagues, dont les limites d’applicabilité ne sont pas toujours claires. Par exemple,” chauve »: pour certains sujets, nous pourrions être enclins à dire qu’ils sont en bonne voie vers la calvitie complète, mais pas encore tout à fait là; d’un autre côté, nous serions réticents à dire qu’ils ne sont pas chauves. Il y a entre les deux cas. Pour de tels cas, nous pourrions dire, par exemple, que la proposition selon laquelle Fredo est chauve n’est ni vraie ni fausse., Certains logiciens ont développé des logiques non bivalentes, pour faire face à ce genre de phénomène linguistique. Certains ajoutent une troisième valeur de vérité: « ni” ou « indéterminé”, par exemple. D’autres introduisent des degrés infinis de vérité (c’est ce qu’on appelle la « logique floue”). Ces logiques s’écartent des approches traditionnelles. Ont-ils donc tort dans un certain sens? Ou ont-ils raison, et les traditionalistes tort? Ou posons-nous même une question sensée lorsque nous demandons si un système logique particulier a raison ou tort?, Pouvons-nous être des soi-disant « pluralistes” logiques, acceptant une variété de logiques incompatibles, selon, par exemple, si elles sont utiles?

bien entendu, ce genre de questions dépasse le cadre de ce texte introductif. Ils sont inclus pour vous donner une idée de jusqu’où on peut prendre l’étude de la logique. La tâche pour l’instant, cependant, est de commencer cette étude.