
Leonardo de Pise (Fibonacci) (C. 1170-1250)
Le 13ème siècle italien Leonardo de Pise, mieux connu par son surnom Fibonacci, était peut-être le mathématicien occidental le plus talentueux du Moyen Âge. On sait peu de choses de sa vie, sauf qu’il était le fils d’un fonctionnaire des douanes et, enfant, il a voyagé en Afrique du Nord avec son père, où il a appris les mathématiques Arabes., À son retour en Italie, il a contribué à diffuser cette connaissance dans toute l’Europe, mettant ainsi en mouvement un rajeunissement dans les mathématiques européennes, qui avaient été en grande partie en sommeil pendant des siècles pendant les âges sombres.
en particulier, en 1202, Il a écrit un livre extrêmement influent appelé « Liber Abaci” (« Livre de calcul”), dans lequel il a promu l’utilisation du système de chiffres Hindou-arabe, décrivant ses nombreux avantages pour les marchands et les mathématiciens par rapport au système maladroit de chiffres romains alors en usage en Europe., Malgré ses avantages évidents, l’adoption du système en Europe a été lente (c’était après tout à l’époque des croisades contre L’Islam, une époque où tout ce qui est arabe était considéré avec beaucoup de suspicion), et les chiffres arabes ont même été interdits dans la ville de Florence en 1299 sous prétexte qu’ils étaient plus faciles à falsifier Cependant, le bon sens a finalement prévalu et le nouveau système a été adopté dans toute l’Europe au 15ème siècle, rendant le système romain obsolète., La notation des barres horizontales pour les fractions a également été utilisée pour la première fois dans ce travail (bien que suivant la pratique arabe de placer la fraction à gauche de l’entier).
séquence de Fibonacci

La Découverte de la célèbre séquence de Fibonacci
Fibonacci est surtout connu, cependant, pour son introduction en Europe d’une séquence de nombres particulière, qui est depuis devenu connu comme les nombres de Fibonacci ou la séquence de Fibonacci., Il a découvert la séquence-la première séquence de nombres récursifs connue en Europe – en examinant un problème pratique dans le « Liber Abaci” impliquant la croissance d’une population hypothétique de lapins basée sur des hypothèses idéalisées. Il a noté que, après chaque génération mensuelle, le nombre de couples de lapins augmentait de 1 à 2 à 3 à 5 à 8 à 13, etc., et a identifié comment la séquence progressait en ajoutant les deux termes précédents (en termes mathématiques, Fn = Fn-1 + Fn-2), une séquence qui pourrait en théorie s’étendre indéfiniment.,
la séquence, qui était en fait connue des mathématiciens Indiens depuis le 6ème siècle, possède de nombreuses propriétés mathématiques intéressantes, et de nombreuses implications et relations de la séquence n’ont été découvertes que plusieurs siècles après la mort de Fibonacci., Par exemple, la séquence se régénère de manière surprenante: chaque troisième nombre F est divisible par 2 (F3 = 2), Chaque quatrième nombre F est divisible par 3 (F4 = 3), chaque cinquième nombre F est divisible par 5 (F5 = 5), chaque sixième nombre f est divisible par 8 (F6 = 8), chaque septième nombre F est divisible par 13 (F7 = 13), etc., Les nombres de la séquence se sont également avérés omniprésents dans la nature: entre autres choses, de nombreuses espèces de plantes à fleurs ont un nombre de pétales dans la séquence de Fibonacci; les arrangements en spirale des ananas se produisent dans 5s et 8s, ceux des pommes de pin dans 8s et 13s, et les graines de têtes de tournesol dans 21s, 34s, 55S ou même des termes plus élevés dans la séquence; etc.,
le nombre d’Or φ
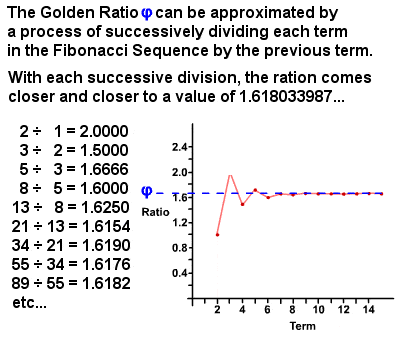
le nombre d’Or φ Peut être dérivé de la séquence de Fibonacci
dans les années 1750, Robert Simson a noté que le rapport de chaque terme de la séquence de Fibonacci au terme précédent approche, avec toujours plus de précision : 1.6180339887 (c’est en fait un nombre irrationnel égal à (1 + √5)⁄2 qui a depuis été calculé à des milliers de décimales)., Cette valeur est appelée le nombre D’Or, également connu sous le nom de moyenne D’or, Section D’or, Proportion Divine, etc., et est généralement désignée par la lettre grecque phi φ (ou parfois la lettre majuscule Phi Φ). Essentiellement, deux quantités sont dans le nombre d’Or si le rapport de la somme des quantités à la plus grande quantité est égal au rapport de la plus grande quantité à la plus petite. Le nombre d’or lui – même a de nombreuses propriétés uniques, telles que 1⁄φ = φ-1 (0.618…) et φ2 = φ + 1 (2.618…), et il existe d’innombrables exemples de cela à la fois dans la nature et dans le monde humain.,
un rectangle avec des côtés dans le rapport de 1 : φ est connu comme un Rectangle D’or, et de nombreux artistes et architectes à travers l’histoire (datant de L’Egypte ancienne et de la Grèce, mais particulièrement populaire dans L’art de la Renaissance de Léonard de Vinci et de ses contemporains) ont proportionné leurs œuvres approximativement en Un arc reliant des points opposés de Rectangles dorés imbriqués de plus en plus petits forme une spirale logarithmique, connue sous le nom de spirale dorée., Le nombre D’or et la spirale D’or peuvent également être trouvés dans un nombre surprenant de cas dans la Nature, des coquilles aux fleurs aux cornes d’animaux aux corps humains aux systèmes d’orage pour compléter les galaxies.,
Il faut se rappeler, cependant, que la séquence de Fibonacci n’était en fait qu’un élément très mineur dans le « Liber Abaci” – en effet, la séquence n’a reçu le nom de Fibonacci qu’en 1877 quand Edouard Lucas a décidé de lui rendre hommage en nommant la série après lui – et que Fibonacci lui-même n’était pas responsable d’identifier aucune des propriétés mathématiques intéressantes de la séquence, sa relation avec la moyenne D’or et les Rectangles D’or et les spirales, etc.,
Multiplication en réseau
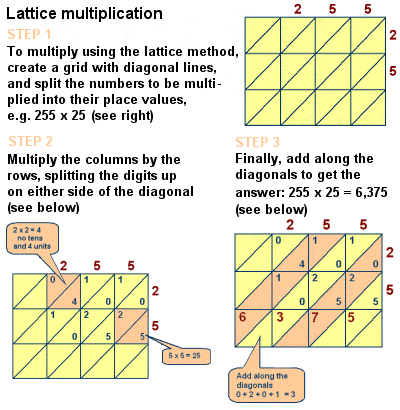
Fibonacci a introduit la multiplication en réseau en Europe
cependant, l’influence du livre sur les mathématiques médiévales est indéniable, et il comprend également des discussions sur un certain nombre d’autres problèmes mathématiques tels que le théorème des preuves géométriques euclidiennes, et une étude des équations linéaires simultanées le long des lignes de Diophante et al-karaji., Il a également décrit la méthode de multiplication en treillis (ou tamis) consistant à multiplier de grands nombres, une méthode – à l’origine mise au point par des mathématiciens islamiques comme Al-Khwarizmi – algorithmiquement équivalente à la multiplication longue.
non plus N’était « Liber Abaci” le seul livre de Fibonacci, bien que ce soit son plus important., Son « Liber Quadratorum » (”Le Livre des carrés »), par exemple, est un livre sur l’algèbre, publié en 1225 dans lequel apparaît une déclaration de ce qui est maintenant appelé L’identité de Fibonacci – parfois aussi connu comme L’identité de Brahmagupta après le mathématicien indien beaucoup plus tôt qui est également arrivé aux mêmes conclusions-que le produit de deux sommes de deux carrés(12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |