Les 5 algorithmes de Clustering que les data Scientists doivent connaître

j’ai récemment lancé un bulletin éducatif axé sur les livres. Book Dives est une newsletter bi-hebdomadaire où, pour chaque nouveau numéro, nous plongeons dans un livre non-fiction. Vous apprendrez les principales leçons du livre et comment les appliquer dans la vie réelle. Vous pouvez vous abonner pour elle ici.

le Clustering est une technique D’apprentissage automatique qui implique le regroupement de points de données. Étant donné un ensemble de points de données, on peut utiliser un algorithme de clustering pour classer chaque point de données dans un groupe spécifique., En théorie, les points de données qui sont dans le même groupe devraient avoir des propriétés et/ou des caractéristiques similaires, tandis que les points de données dans différents groupes devraient avoir des propriétés et/ou des caractéristiques très différentes. Le Clustering est une méthode d’apprentissage non supervisé et est une technique courante pour l’analyse de données statistiques utilisée dans de nombreux domaines.

en science des données, nous pouvons utiliser l’analyse de clustering pour obtenir des informations précieuses à partir de nos données en voyant dans quels groupes les points de données tombent lorsque nous appliquons un algorithme de clustering., Aujourd’hui, nous allons examiner 5 algorithmes de clustering populaires que les data scientists doivent connaître et leurs avantages et inconvénients!

K-means

K-means est probablement le plus bien connu algorithme de clustering. Il est enseigné dans de nombreux cours d’introduction à la science des données et à l’apprentissage automatique. C’est facile à comprendre et à implémenter dans le code! Découvrez le graphique ci-dessous.,

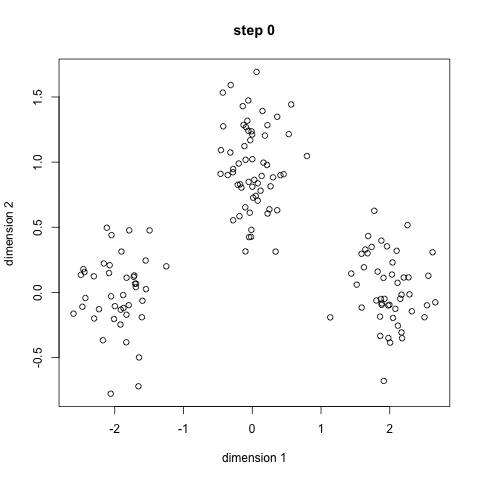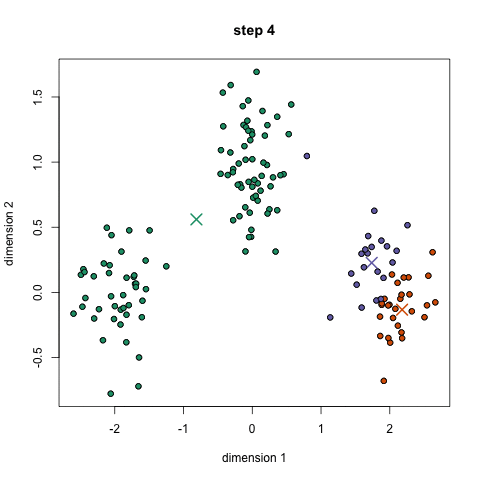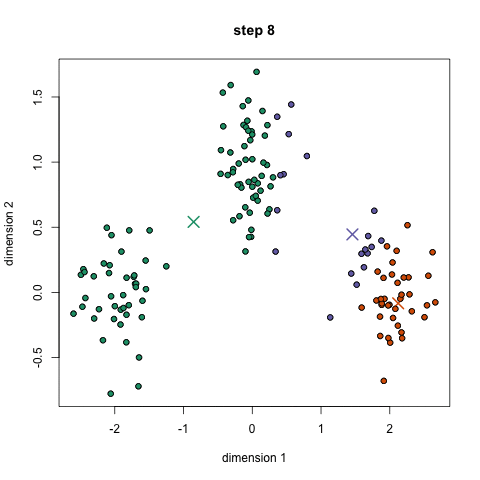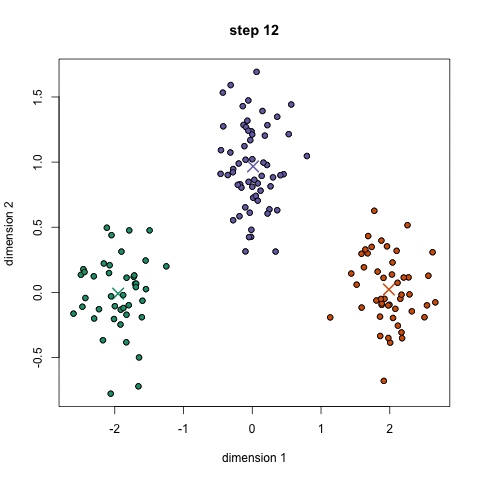
1. Pour commencer, nous avons d’abord sélectionner un certain nombre de classes/groupes à l’utilisation et au hasard initialiser leurs respectives des points centraux. Pour déterminer le nombre de classes à utiliser, il est bon de jeter un coup d’œil rapide aux données et d’essayer d’identifier les groupements distincts. Les points centraux sont des vecteurs de même longueur que chaque vecteur de point de données et sont les « X” dans le graphique ci-dessus.,
2. chaque point de données est classé en calculant la distance entre ce point et chaque centre de groupe, puis en classant le point dans le groupe dont le centre est le plus proche.
3. sur la base de ces points classifiés, on recalcule le centre du groupe en prenant la moyenne de tous les vecteurs du groupe.
4. répétez ces étapes pour un nombre défini d’itérations ou jusqu’à ce que les centres de groupe ne changent pas beaucoup entre les itérations. Vous pouvez également choisir d’initialiser aléatoirement les centres de groupe à quelques reprises, puis sélectionner l’exécution qui semble avoir fourni les meilleurs résultats.,

K-Means a l’avantage d’être assez rapide, car tout ce que nous faisons vraiment est de calculer les distances entre les points et les centres de groupe; très peu de calculs! Il a donc une complexité linéaire O (n).

d’autre part, K-means a quelques inconvénients. Tout d’abord, vous devez sélectionner le nombre de groupes/classes. Ce n’est pas toujours trivial et idéalement avec un algorithme de clustering, nous voudrions qu’il les comprenne pour nous car le but est d’obtenir un aperçu des données., K-means commence également par un choix aléatoire de centres de cluster et peut donc donner différents résultats de clustering sur différentes exécutions de l’algorithme. Ainsi, les résultats peuvent ne pas être reproductibles et manquer de cohérence. D’autres méthodes de clustering sont plus cohérentes.

K-médianes est un autre algorithme de clustering lié aux K-moyennes, sauf qu’au lieu de recalculer les points centraux du groupe en utilisant la moyenne, nous utilisons le vecteur médian du groupe., Cette méthode est moins sensible aux valeurs aberrantes (en raison de l’utilisation de la médiane) mais est beaucoup plus lente pour les ensembles de données plus volumineux, car un tri est requis à chaque itération lors du calcul du vecteur médian.

mean-Shift Clustering

Mean shift clustering est un algorithme basé sur une fenêtre coulissante qui tente de trouver des zones denses de points de données. Il s’agit d’un algorithme basé sur un centroïde, ce qui signifie que l’objectif est de localiser les points centraux de chaque groupe/classe, ce qui fonctionne en mettant à jour les candidats pour que les points centraux soient la moyenne des points dans la fenêtre coulissante., Ces fenêtres candidates sont ensuite filtrées dans une étape de post-traitement pour éliminer les quasi-doublons, formant l’ensemble final des points centraux et leurs groupes correspondants. Découvrez le graphique ci-dessous.

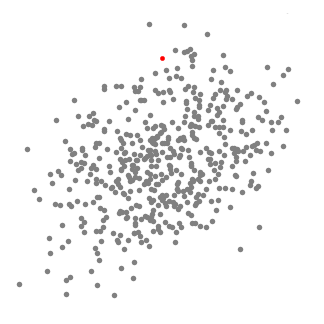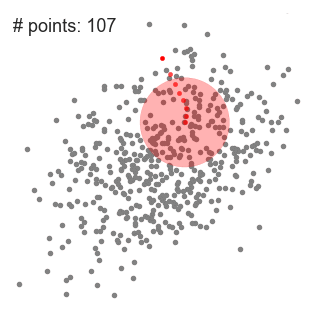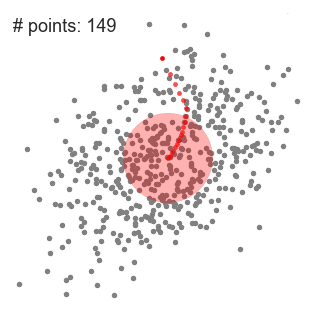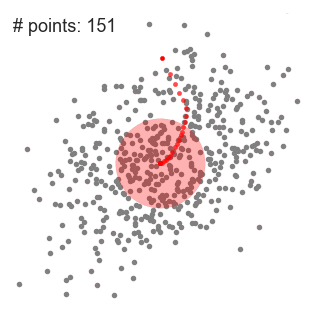
1. Pour expliquer mean-shift, nous allons considérer un ensemble de points dans un espace à deux dimensions comme l’illustration ci-dessus., Nous commençons par une fenêtre coulissante circulaire centrée en un point C (choisi au hasard) et ayant le rayon r comme noyau. Mean shift est un algorithme d’escalade qui consiste à déplacer ce noyau de manière itérative vers une région de densité plus élevée à chaque étape jusqu’à la convergence.
2. à chaque itération, la fenêtre coulissante est décalée vers des régions de densité plus élevée en déplaçant le point central vers la moyenne des points de la fenêtre (d’où le nom). La densité à l’intérieur de la fenêtre coulissante est proportionnelle au nombre de points à l’intérieur d’elle., Naturellement, en passant à la moyenne des points de la fenêtre, il se déplacera progressivement vers des zones de densité de points plus élevée.
3. nous continuons à déplacer la fenêtre coulissante en fonction de la moyenne jusqu’à ce qu’il n’y ait pas de direction à laquelle un décalage peut accueillir plus de points à l’intérieur du noyau. Consultez le graphique ci-dessus; nous continuons à déplacer le cercle jusqu’à ce que nous n’augmentions plus la densité (c’est-à-dire le nombre de points dans la fenêtre).
4. Ce processus des étapes 1 à 3 se fait avec de nombreuses fenêtres coulissantes jusqu’à ce que tous les points se trouvent dans une fenêtre., Lorsque plusieurs fenêtres coulissantes se chevauchent, la fenêtre contenant le plus de points est conservée. Les points de données sont ensuite regroupés en fonction de la fenêtre coulissante dans laquelle ils résident.

Une illustration de l’ensemble du processus de bout en bout avec toutes les fenêtres coulissantes est indiqué ci-dessous. Chaque point noir représente le centroïde d’une fenêtre coulissante et chaque point gris est un point de données.,

Contrairement à K-means, il n’est pas nécessaire de sélectionner le nombre de clusters comme mean-shift découvre automatiquement. C’est un avantage énorme. Le fait que les centres de cluster convergent vers les points de densité maximale est également tout à fait souhaitable car il est assez intuitif à comprendre et s’intègre bien dans un sens naturellement axé sur les données., L’inconvénient est que la sélection de la taille de la fenêtre/rayon « r” peut être non négligeable.

Clustering Spatial basé sur la densité D’Applications avec bruit (DBSCAN)

DBSCAN est un algorithme de clustering basé sur la densité similaire à mean-shift, mais avec quelques avantages notables. Découvrez un autre graphique de fantaisie ci-dessous et commençons!,

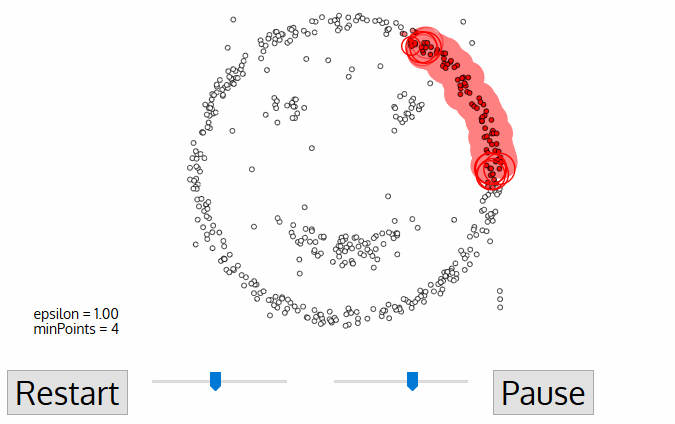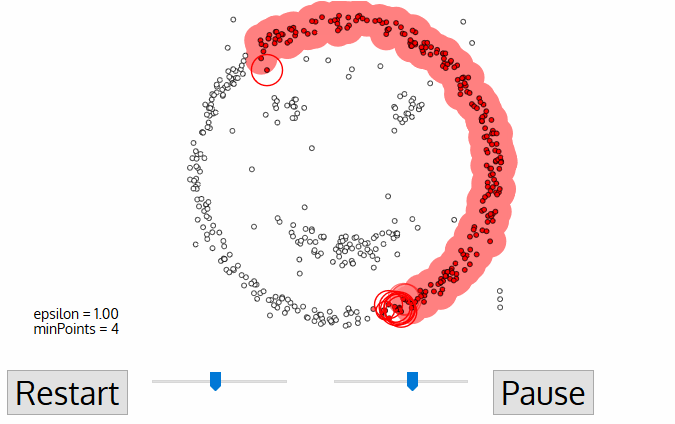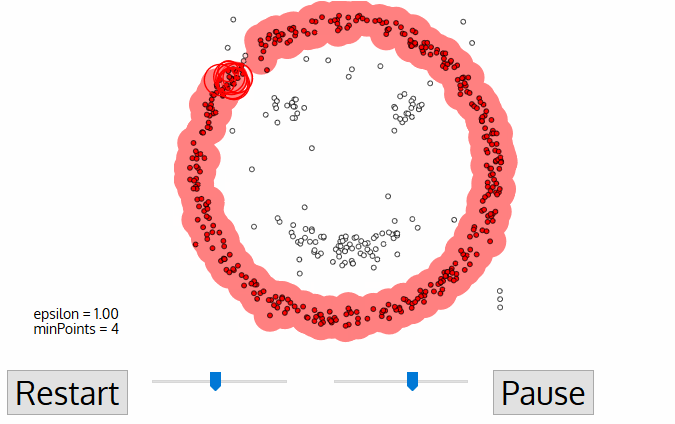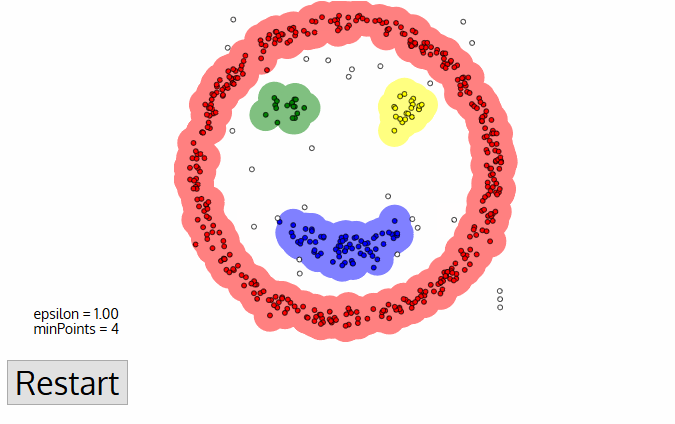
1. DBSCAN commence avec un arbitraire de départ point de données qui n’a pas été visité. Le voisinage de ce point est extrait à l’aide d’une distance Epsilon ε (Tous les points qui sont dans la distance ε sont des points de voisinage).,
2. S’il y a un nombre suffisant de points (selon les minPoints) dans ce voisinage alors le processus de clustering commence et le point de données actuel devient le premier point dans le nouveau cluster. Sinon, le point sera étiqueté comme bruit (plus tard, ce point bruyant pourrait devenir la partie du cluster). Dans les deux cas, ce point est marqué comme « visité”.
3. Pour ce premier point du nouveau cluster, les points situés dans son voisinage de distance ε font également partie du même cluster., Cette procédure consistant à faire appartenir tous les points du voisinage ε au même cluster est ensuite répétée pour tous les nouveaux points qui viennent d’être ajoutés au groupe de cluster.
4. ce processus des étapes 2 et 3 est répété jusqu’à ce que tous les points du cluster soient déterminés, c’est-à-dire que tous les points du voisinage ε du cluster ont été visités et étiquetés.
5. Une fois que nous avons terminé avec le cluster actuel, un nouveau point non visité est récupéré et traité, ce qui conduit à la découverte d’un cluster ou d’un bruit supplémentaire. Ce processus se répète jusqu’à ce que tous les points soient marqués comme visités., Car, à la fin de ce tous les points ont été visités, chaque point aura été marqué comme appartenant à un cluster ou de bruit.

DBSCAN présente de grands avantages par rapport aux autres algorithmes de clustering. Premièrement, il ne nécessite pas du tout un nombre de clusters PE-set. Il identifie également les valeurs aberrantes comme des bruits, contrairement à mean-shift qui les jette simplement dans un cluster même si le point de données est très différent. De plus, il peut très bien trouver des grappes de taille arbitraire et de forme arbitraire.,

le principal inconvénient de DBSCAN est qu’il ne fonctionne pas aussi bien que les autres lorsque les clusters sont de densité variable. En effet, le réglage du seuil de distance ε et des points minimaux pour identifier les points de voisinage variera d’un cluster à l’autre lorsque la densité varie. Cet inconvénient se produit également avec des données de dimensions très élevées car, là encore, le seuil de distance ε devient difficile à estimer.,

Clustering Expectation–Maximization (EM) à l’aide de modèles de mélange gaussiens (GMM)

l’un des principaux inconvénients de K-Means est son utilisation naïve de la valeur moyenne pour le centre du cluster. Nous pouvons voir pourquoi ce n’est pas la meilleure façon de faire les choses en regardant l’image ci-dessous. Sur le côté gauche, il semble assez évident à l’œil humain qu’il y a deux amas circulaires avec un rayon différent’ centré à la même moyenne. K-Means ne peut pas gérer cela car les valeurs moyennes des clusters sont très proches les unes des autres., K-Means échoue également dans les cas où les clusters ne sont pas circulaires, encore une fois en raison de l’utilisation de la moyenne comme centre de cluster.

Modèles de mélanges gaussiens (Mgm), nous donner plus de flexibilité que les K-Means. Avec GMMs, nous supposons que les points de données sont distribués gaussiens; c’est une hypothèse moins restrictive que de dire qu’ils sont circulaires en utilisant la moyenne., De cette façon, nous avons deux paramètres pour décrire la forme des grappes: la moyenne et l’écart type! En prenant un exemple en deux dimensions, cela signifie que les grappes peuvent prendre n’importe quel type de forme elliptique (puisque nous avons un écart type dans les directions x et y). Ainsi, chaque distribution gaussienne est affectée à un seul cluster.

pour trouver les paramètres de la gaussienne pour chaque cluster (par exemple la moyenne et l’écart type), nous allons utiliser un algorithme d’optimisation appelé Expectation–Maximization (EM)., Regardez le graphique ci-dessous pour illustrer les gaussiens ajustés aux grappes. Ensuite, nous pouvons procéder au processus de clustering D’attente–maximisation à l’aide de GMM.

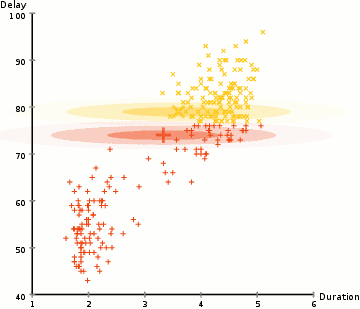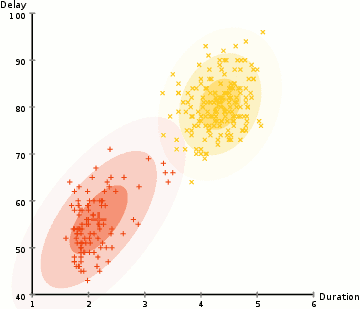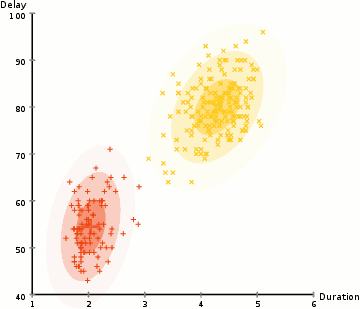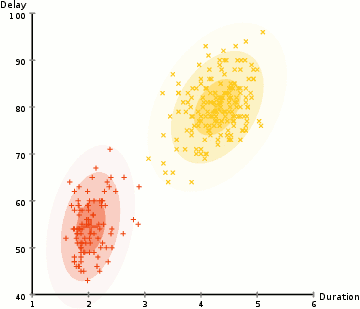
1. Nous commençons par sélectionner le nombre de clusters (comme K-means) et au hasard de l’initialisation de la distribution Gaussienne de paramètres pour chaque cluster., On peut essayer de fournir une bonne estimation des paramètres initiaux en examinant rapidement les données. Bien que notez, comme on peut le voir dans le graphique ci-dessus, ce n’est pas nécessaire à 100% car les gaussiens commencent Notre comme très pauvres mais sont rapidement optimisés.
2. compte tenu de ces distributions gaussiennes pour chaque cluster, calculez la probabilité que chaque point de données appartient à un cluster particulier. Plus un point est proche du centre de la gaussienne, plus il appartient probablement à ce cluster., Cela devrait avoir un sens intuitif car avec une distribution gaussienne, nous supposons que la plupart des données se trouvent plus près du centre du cluster.
3. sur la base de ces probabilités, nous calculons un nouvel ensemble de paramètres pour les distributions gaussiennes de sorte que nous maximisons les probabilités des points de données dans les clusters. Nous calculons ces nouveaux paramètres en utilisant une somme pondérée des positions des points de données, où les poids sont les probabilités du point de données appartenant à ce cluster particulier., Pour expliquer cela visuellement, nous pouvons regarder le graphique ci-dessus, en particulier le cluster jaune à titre d’exemple. La distribution commence aléatoirement lors de la première itération, mais nous pouvons voir que la plupart des points jaunes sont à droite de cette distribution. Lorsque nous calculons une somme pondérée par les probabilités, même s’il y a des points près du centre, la plupart d’entre eux sont à droite. Ainsi, naturellement, la moyenne de la distribution est décalée plus près de cet ensemble de points. Nous pouvons également voir que la plupart des points sont « de haut en bas à droite »”, Par conséquent, l’écart type change pour créer une ellipse plus adaptée à ces points, afin de maximiser la somme pondérée par les probabilités.
4. Les étapes 2 et 3 sont répétées de manière itérative jusqu’à la convergence, où les distributions ne changent pas beaucoup d’itération en itération.

l’utilisation de GMM présente 2 Avantages clés. Premièrement, les GMM sont beaucoup plus flexibles en termes de covariance de cluster que les k-moyennes; en raison du paramètre d’écart-type, les clusters peuvent prendre n’importe quelle forme d’ellipse, plutôt que d’être limités à des cercles., K-Means est en fait un cas particulier de GMM dans lequel la covariance de chaque cluster le long de toutes les dimensions approche 0. Deuxièmement, puisque les GMM utilisent des probabilités, ils peuvent avoir plusieurs clusters par point de données. Donc, si un point de données est au milieu de deux clusters qui se chevauchent, nous pouvons simplement définir sa classe en disant qu’il appartient X-pour cent à la classe 1 et Y-pour cent à la classe 2. C’est-à-dire que les GMM soutiennent l’adhésion mixte.

Clustering hiérarchique agglomératif

les algorithmes de clustering hiérarchique se divisent en 2 catégories: de haut en bas ou de bas en haut., Les algorithmes ascendants traitent chaque point de données comme un seul cluster au départ, puis fusionnent successivement (ou agglomèrent) des paires de clusters jusqu’à ce que tous les clusters aient été fusionnés en un seul cluster contenant tous les points de données. Le clustering hiérarchique ascendant est donc appelé clustering agglomératif hiérarchique ou HAC. Cette hiérarchie de clusters est représentée sous la forme d’un arbre (ou dendrogramme). La racine de l’arbre est la grappe unique qui rassemble tous les échantillons, les feuilles étant les grappes avec un seul échantillon., Découvrez le graphique ci-dessous avant de passer à l’algorithme qui suit

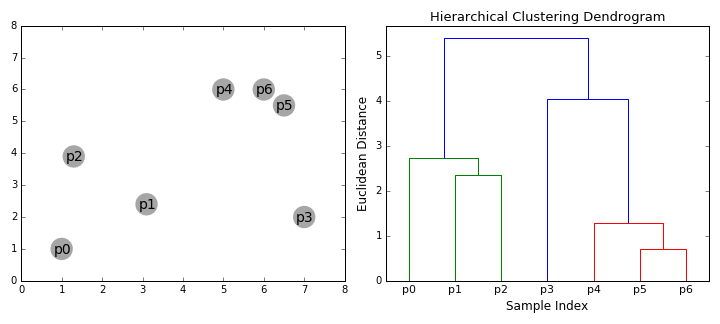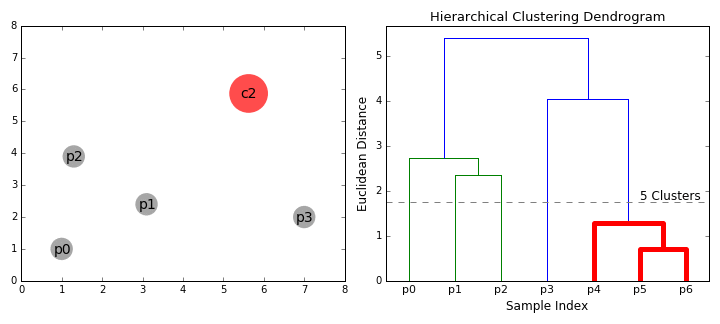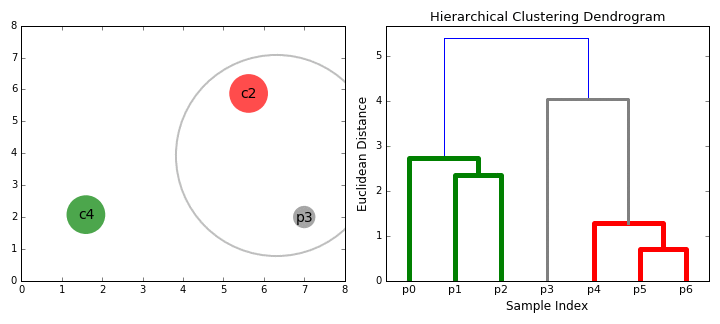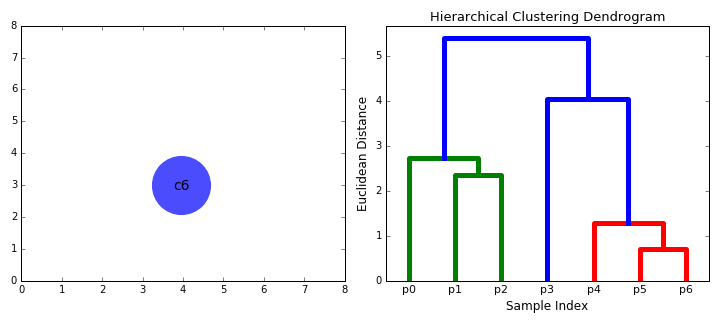
1. On commence par traiter chaque point de données comme un seul cluster je.e si il y a X points de données dans notre base de données, puis nous avons X clusters. Nous sélectionnons ensuite une mesure de distance qui mesure la distance entre deux clusters., À titre d’exemple, nous utiliserons la liaison moyenne qui définit la distance entre deux clusters comme étant la distance moyenne entre les points de données du premier cluster et les points de données du second cluster.
2. à chaque itération, nous combinons deux clusters en un seul. Les deux clusters à combiner sont choisis comme étant ceux ayant le plus petit lien moyen. C’est-à-dire que selon notre métrique de distance sélectionnée, ces deux grappes ont la plus petite distance entre elles et sont donc les plus similaires et doivent être combinées.
3. l’Étape 2 est répétée jusqu’à ce que nous atteignions la racine de l’arbre I.,e nous n’avons qu’un cluster qui contient tous les points de données. De cette façon, nous pouvons sélectionner le nombre de clusters que nous voulons à la fin, simplement en choisissant quand arrêter de combiner les clusters, c’est-à-dire quand nous arrêtons de construire l’arbre!

le clustering hiérarchique ne nous oblige pas à spécifier le nombre de clusters et nous pouvons même sélectionner le nombre de clusters qui semble le mieux puisque nous construisons un arbre. De plus, l’algorithme n’est pas sensible au choix de la mesure de distance; tous ont tendance à fonctionner également bien alors qu’avec d’autres algorithmes de clustering, le choix de la mesure de distance est critique., Un cas d’utilisation particulièrement bon des méthodes de clustering hiérarchique est lorsque les données sous-jacentes ont une structure hiérarchique et que vous souhaitez récupérer la hiérarchie; d’autres algorithmes de clustering ne peuvent pas le faire. Ces avantages du clustering hiérarchique se font au prix d’une efficacité moindre, car il a une complexité temporelle de O(n3), contrairement à la complexité linéaire de K-Means et de GMM.