Learning Outcomes
- familiarisez-vous avec l’histoire des systèmes numériques positionnels
- identifiez les bases qui ont été utilisées dans les systèmes numériques historiquement
- convertir des nombres entre bases
- utilisez deux méthodes différentes pour convertir des nombres entre bases
Background
comme vous pouvez L’imaginer, le développement d’un système de base est une étape importante pour rendre le processus de comptage plus efficace., Notre propre système base-ten est probablement né du fait que nous avons 10 doigts (y compris les pouces) sur deux mains. C’est une évolution naturelle. Cependant, d’autres civilisations ont eu une variété de bases autres que dix. Par exemple, les indigènes du Queensland ont utilisé un système de base-deux, comptant comme suit: « un, deux, deux et un, deux deux, beaucoup.” Certains Modernes Tribus d’Amérique du Sud ont une base-cinq système de comptage de cette façon: « un, deux, trois, quatre, main, main et un, et deux,” et ainsi de suite. Les Babyloniens utilisaient un système de base soixante (sexigésimal)., Dans ce chapitre, nous terminons avec un exemple spécifique d’une civilisation qui a réellement utilisé un système de base autre que 10.
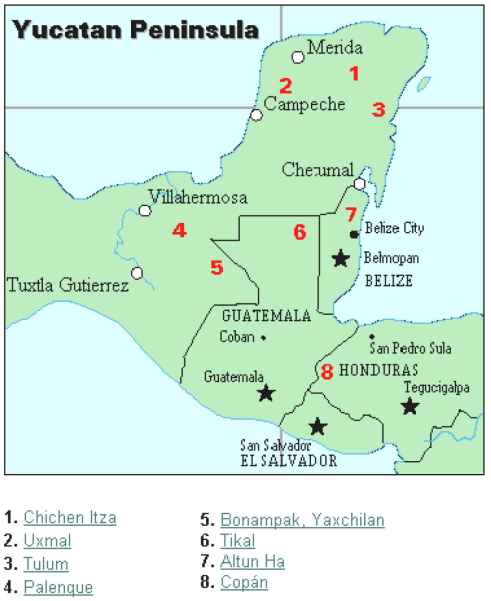la civilisation Maya est généralement datée de 1500 AEC à 1700 CE. La péninsule du Yucatan (voir figure 16) au Mexique a été le théâtre du développement de l’une des civilisations les plus avancées du monde antique. Les Mayas avaient un système rituel sophistiqué qui était supervisé par une classe sacerdotale. Cette classe de prêtres a développé une philosophie avec le temps comme divin et éternel., Le calendrier, et les calculs qui s’y rapportent, étaient donc très importants pour la vie rituelle de la classe sacerdotale, et donc du peuple Maya. En fait, une grande partie de ce que nous savons de cette culture provient de leurs enregistrements de calendrier et de données astronomiques. Une autre source importante d’information sur les Mayas est les écrits du Père Diego de Landa, qui est allé au Mexique comme missionnaire en 1549.
il y avait deux systèmes de chiffres développés par les Mayas—un pour les gens ordinaires et un pour les prêtres., Non seulement ces deux systèmes utilisaient des symboles différents, mais ils utilisaient également des systèmes de base différents. Pour les prêtres, le système de numération était régi par le rituel. Les jours de l’année étaient considérés comme des dieux, de sorte que les symboles formels des jours étaient des têtes décorées, comme l’échantillon à gauche puisque le calendrier de base était basé sur 360 jours, le système de chiffres sacerdotaux utilisait un système de base mixte employant des multiples de 20 et 360. Cela crée un système déroutant, dont nous sauterons les détails.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the « common” people, which used a more consistent base system., Comme nous l’avons dit plus tôt, les Mayas utilisaient un système de base-20, appelé système « vigésimal”. Comme notre système, il est positionnel, ce qui signifie que la position d’un symbole numérique indique sa valeur de place. Dans le tableau suivant, vous pouvez voir la valeur de lieu dans son format vertical.
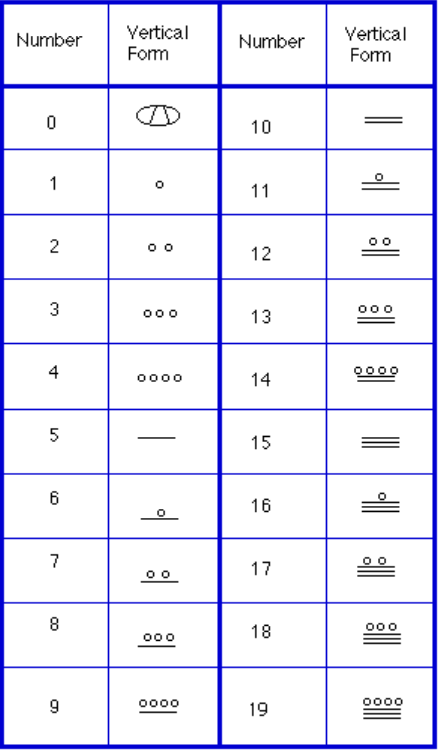
pour écrire des nombres, il n’y avait que trois symboles nécessaires dans ce système. Une barre horizontale représentait la quantité 5, un point représentait la quantité 1 et un symbole spécial (considéré comme une coquille) représentait zéro., Le système Maya a peut-être été le premier à utiliser zéro comme espace réservé/nombre. Les 20 premiers numéros sont indiqués dans le tableau à droite.
contrairement à notre système, où ceux qui sont placés commencent à droite puis se déplacent vers la gauche, les systèmes Mayas placent ceux qui sont en bas d’une orientation verticale et montent à mesure que la valeur de place augmente.
lorsque les nombres sont écrits sous forme verticale, il ne doit jamais y avoir plus de quatre points en un seul endroit. Lors de l’écriture de nombres Mayas, chaque groupe de cinq points devient une barre., En outre, il ne devrait jamais y avoir plus de trois barres en un seul endroit-quatre barres seraient converties en un point à l’endroit suivant. C’est la même chose que 10 se convertir en un 1 à l’endroit suivant lorsque nous portons lors de l’addition.
Exemple
Quelle est la valeur de ce nombre, qui est montré dans la forme verticale?
Exemple
Quelle est la valeur de la suite de Maya nombre?,
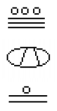
Essayer
Convertir les Mayas numéro ci-dessous pour la base 10.,
Exemple
conversion de la base 10 du nombre 357510 de chiffres Maya.
écrire des nombres avec des bases supérieures à 10
lorsque la base d’un nombre est supérieure à 10, séparez chaque « chiffre” par une virgule pour que la séparation des chiffres soit claire.
par exemple, en base 20, pour écrire le nombre correspondant à 17 × 202 + 6 × 201 + 13 × 200, nous écririons 17,6,1320.
dans la vidéo suivante, nous présentons plus d’exemples de la façon d’écrire des nombres en utilisant des chiffres Mayas ainsi que de convertir des chiffres écrits en Maya pour en base 10.,
La vidéo suivante montre plus d’exemples de conversion de nombres de base 10 en chiffres Mayas.
ajout de nombres Mayas
lors de l’ajout de nombres Mayas ensemble, nous adopterons un schéma que les Mayas n’ont probablement pas utilisé mais qui nous facilitera un peu la vie.
Exemple
Ajouter, dans les Mayas, les numéros 37 et 29:
Essayer
Essayez d’ajouter 174 et 78 Maya en convertissant d’abord à Maya numéros et ensuite de travailler entièrement à l’intérieur de ce système. N’ajoutez pas en base-dix (décimal) jusqu’à la toute fin lorsque vous vérifiez votre travail.
Dans la dernière vidéo, nous montrons des exemples plus de l’ajout de chiffres Maya.,
Dans ce module, nous avons brièvement esquissé le développement des nombres et de notre système de comptage, en mettant l’accent sur la partie « brève”. Il existe de nombreuses sources d’information et de recherche qui remplissent de nombreux volumes de livres sur ce sujet. Malheureusement, nous ne pouvons pas commencer à couvrir toutes les informations disponibles.
Nous avons seulement rayé la surface de la richesse de la recherche et de l’information qui existe sur le développement des nombres et du comptage à travers l’histoire humaine., Ce qui est important à noter est que le système que nous utilisons chaque jour est un produit de milliers d’années de progrès et de développement. Il représente les contributions de nombreuses civilisations et cultures. Il ne nous descend pas du ciel, un don des dieux. Ce n’est pas la création d’un éditeur de manuels. Il est en effet aussi humain que nous sommes, comme le reste des mathématiques. Derrière chaque symbole, formule et règle, il y a un visage humain à trouver, ou du moins à chercher.
En outre, nous espérons que vous avez maintenant une appréciation de base de la façon dont les systèmes numériques intéressants et diversifiés peuvent obtenir., En outre, nous sommes à peu près sûrs que vous avez également commencé à reconnaître que nous tenons notre propre système de numéros pour acquis tellement que lorsque nous essayons de nous adapter à d’autres systèmes ou bases, nous nous retrouvons vraiment à devoir nous concentrer et réfléchir à ce qui se passe.