en Géométrie, un polyèdre est une figure d’espace fermé dont les faces sont des polygones. Le mot polyèdre a des origines grecques, ce qui signifie de nombreux visages. Ce qui suit sont quelques exemples de polyèdres.
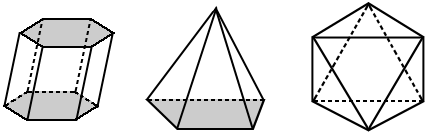
Caractéristiques d’un polyèdre
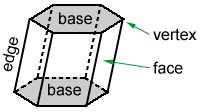
Les polygones qui forme un polyèdre sont appelés les visages. Les segments de ligne créés par deux faces se croisant sont appelés arêtes. Les sommets sont des points où trois arêtes ou plus se rencontrent.,
Le prisme hexagonal ci-dessus est un polyèdre qui a 6 faces latérales qui sont des parallélogrammes, et 2 faces en haut et en bas, appelés bases, qui sont des hexagones.
le Théorème d’Euler
le Théorème d’Euler montre une relation entre le nombre de faces, de sommets et d’arêtes d’un polyèdre., Elle stipule que la somme des faces et des sommets moins le nombre d’arêtes est toujours égale à deux:
F + V – E = 2
où F est le nombre de faces, V est le nombre de sommets, et E est le nombre d’arêtes d’un polyèdre.
Exemple:
Pour le prisme hexagonal indiqué ci-dessus, F = 8 (six faces latérales + deux bases), V = 12, et E = 18:
8 + 12 – 18 = 2
Classifications de polyèdres
Polyèdres peuvent être classés de plusieurs façons. Par exemple, ils peuvent être classés comme polyèdres réguliers et irréguliers., Un polyèdre régulier est un polyèdre dont les faces sont toutes des polygones réguliers congruents; tout polyèdre qui ne remplit pas ces conditions est considéré comme irrégulier.
les polyèdres peuvent également être classés comme convexes et concaves. Un polyèdre concave possède au moins une face qui est un polygone concave. Un polyèdre qui n’est pas concave, est convexe. Les polyèdres peuvent également être classés en fonction du nombre de faces qu’ils possèdent. Par exemple, un tétraèdre a 4 faces, un pentaèdre a 5 faces, et un hexaèdre a 6 faces.,
Voici une liste de termes souvent utilisés pour décrire les polyèdres en fonction de leurs caractéristiques.
prismes
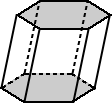
Les prismes sont des polyèdres qui ont deux faces congruentes, appelées bases, situées dans des plans parallèles. Un prisme est généralement nommé par la forme de ses bases polygonales. Les faces latérales (les côtés qui ne sont pas des bases) sont des parallélogrammes, des rectangles ou des carrés.,
| Régulier prism | Irrégulière prism |
|---|---|
 |
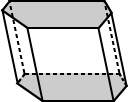 |
| Les bases pour le prisme hexagonal ci-dessus ont des bases qui sont des hexagones réguliers. | les bases du prisme hexagonal ci-dessus sont des hexagonaux irréguliers. |
pyramides
Les Pyramides sont des polyèdres qui ont un polygone comme base et des triangles comme toutes ses autres faces.Une pyramide est également généralement nommée par la forme de sa base polygonale.,
| pyramide Régulière | Irrégulière pyramide |
|---|---|
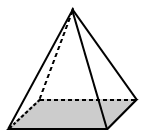 |
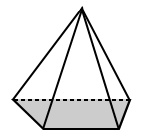 |
| La base de la place de la pyramide ci-dessus a une base qui est un carré (un polygone régulier). | la base de la pyramide trapézoïdale ci-dessus est un trapèze avec des côtés inégaux (c’est donc un polygone irrégulier). |
polyèdres Réguliers
Un polyèdre régulier est un polyèdre dont les faces sont toutes en harmonie, les polygones réguliers., Un polyèdre régulier est nommé en fonction de son nombre de faces. Il n’y a que cinq polyèdres qui sont des polyèdres réguliers; ceux-ci sont appelés solides platoniques.
Les cinq solides Platoniciens
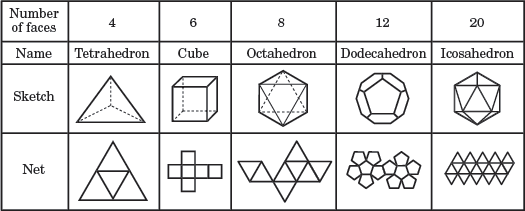
Dans le diagramme ci-dessus, chaque polyèdres réguliers est nommé en fonction de son nombre de faces. Le filet sous chaque croquis montre une image 2D de toutes les faces du polyèdre.
la Plupart des prismes sont généralement pas considérés comme des polyèdres réguliers., Un cube est le seul prisme régulier qui peut également être considéré comme un polyèdre régulier.
de Même, un tétraèdre régulier est la seule pyramide régulière qui est aussi un polyèdre régulier.