Ressources connexes: science des matériaux
équations du module de Section et Calculatrices formes courantes
résistance des matériaux | déformation et contrainte du faisceau
le module de Section est une propriété géométrique pour une section donnée utilisée dans la conception de poutres ou Les autres propriétés géométriques utilisées dans la conception comprennent la zone de tension, le rayon de giration pour la compression et le moment d’inertie pour la rigidité., Toute relation entre ces propriétés dépend fortement de la forme en question. Les équations pour les modules de section des formes communes sont données ci-dessous. Il existe deux types de modules de section, le module de section élastique (s) et le module de section plastique (Z).
Pour la conception générale, le module de flexion élastique est utilisé, appliquer jusqu’à la limite d’élasticité pour la plupart des métaux et d’autres matériaux.
le module de section élastique est défini comme S = I / y, où I est le deuxième moment d’aire (ou moment d’inertie) et y est la distance de l’axe neutre à une fibre donnée., Il est souvent rapporté en utilisant y = c, où c est la distance entre l’axe neutre et la fibre la plus extrême , comme on le voit dans le tableau ci-dessous. Il est également souvent utilisé pour déterminer le moment de rendement (My) tel que My = s × σy, où σy est la limite d’élasticité du matériau.,p>
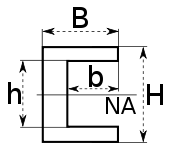
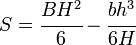
Calculator:
Section Modulus Channel Shape Center Neutral Axis Calculator
Plastic Section Modulus (PNA)
The Plastic section modulus is used for materials where (irreversible) plastic behavior is dominant., La majorité des modèles ne rencontrent pas intentionnellement ce comportement.
le module de section plastique dépend de l’emplacement de l’axe neutre plastique (PNA). Le PNA est défini comme l’axe qui divise la section transversale de telle sorte que la force de compression de la zone en compression soit égale à la force de tension de la zone en tension. Ainsi, pour les sections avec une contrainte de rendement constante, la surface au-dessus et au-dessous du PNA sera égale, mais pour les sections composites, ce n’est pas nécessairement le cas.,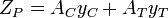
- section Module équations et Calculatrices
- section Propriétés rayon de giration Cas 1 – 10
- section Propriétés rayon de giration cas 11 – 16
- section Propriétés rayon de giration cas 17 – 22
- section Propriétés rayon de giration cas 23 – 27
- section Propriétés rayon cas de giration 28 – 31
- propriétés de section rayon de giration cas 32 – 34
- propriétés de section rayon de giration cas 35 – 37

![]()