Lorsqu’une fraction « normale” contient des fractions dans le numérateur ou le dénominateur ou les deux, alors nous la considérons comme une fraction complexe. Ce type de fraction est également connu sous le nom de fraction composée.
Il existe deux méthodes utilisées pour simplifier ce genre de fraction.
Méthode 1
les principales étapes:
- Créer une seule fraction du numérateur et du dénominateur.,
- appliquer la règle de division des fractions en multipliant le numérateur par la réciproque ou l’inverse du dénominateur.
- Simplifier, si nécessaire.
Méthode 2
les principales étapes:
- Trouver le plus petit Dénominateur Commun (PPDC) de tous les dénominateurs des fractions complexes.
- multipliez cet écran LCD au numérateur et au dénominateur de la fraction complexe.
- Simplifier, si nécessaire.,
Après avoir parcouru quelques exemples, vous devez vous rendre compte que la méthode 2 est bien meilleure que la méthode 1 car il faut presque toujours moins d’étapes pour arriver à la réponse finale.
exemples de simplification des Fractions Complexes
exemple 1: Simplifiez la fraction complexe ci-dessous.
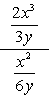
- Utilisation de la Méthode 1
à la Fois le numérateur et le dénominateur de la fraction complexe sont déjà exprimés comme de simples fractions. C’est génial!,

La prochaine étape à faire est d’appliquer de la division de la règle en multipliant le numérateur par l’inverse du dénominateur. Terminez en annulant les facteurs communs pour obtenir la réponse finale.
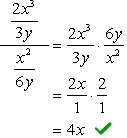
- Utilisation de la Méthode 2
Trouver l’écran LCD de l’ensemble du problème, qui est, l’écran LCD du haut et du bas des dénominateurs.,

Depuis l’écran LCD de 3 ans et 6y est juste \textbf{6y}, nous allons maintenant, multipliez le complexe numérateur et le dénominateur par ce LCD. Après cela, nous pouvons nous attendre à ce que le problème soit réduit à une seule fraction qui peut être simplifiée comme d’habitude.
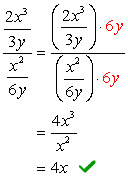
Exemple 2: Simplifier la fraction complexe ci-dessous.,
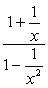
- Utilisation de la Méthode 1
Dans cette méthode, nous voulons créer une fraction unique à la fois au numérateur et au dénominateur. Évidemment, ce problème nous obligerait à le faire d’abord avant d’effectuer la division.
ajoutez les fractions du numérateur et soustrayez celles du dénominateur.,
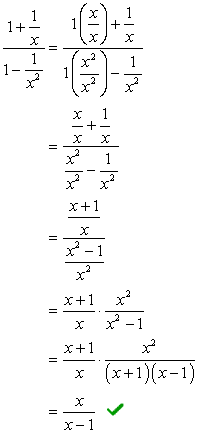
- Utilisation de la Méthode 2
en Regardant les dénominateurs \large{x} et \large{x^2}, l’écran LCD doit être \large{x^2} Multiplier en haut et en bas par ce LCD.
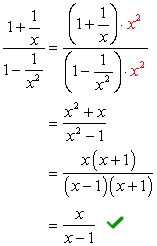
Exemple 3: Simplifier la fraction complexe ci-dessous.,
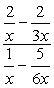
- Utilisation de la Méthode 1
Créer une seule fractions à la fois le numérateur et le dénominateur, puis suivi par la division de fractions.
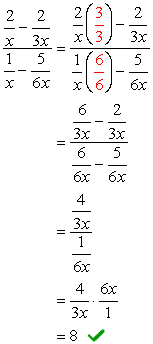
- En utilisant la méthode 2
l’affichage à cristaux liquides global des dénominateurs est \color{red}6x. utilisez-le pour multiplier les expressions en haut et en bas.,
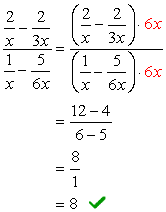
Exemple 4: Simplifier la fraction complexe ci-dessous.
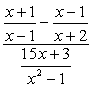
Pour résoudre ce problème, nous allons utiliser la Méthode 1 uniquement.
le problème nécessite d’appliquer la méthode FOIL (multiplication de deux binômes) et une factorisation simple de trinôme. Cela peut sembler un peu intimidant au début; cependant, si vous faites attention aux détails, je vous garantis que ce n’est pas si mal.,
Si vous observez, le dénominateur complexe est déjà sous la forme que nous voulons – avoir un symbole fractionnaire. Cela signifie que nous devons travailler un peu sur le complexe numérateur. Notre prochaine étape serait de transformer le numérateur complexe en une fraction” simple » ou unique.
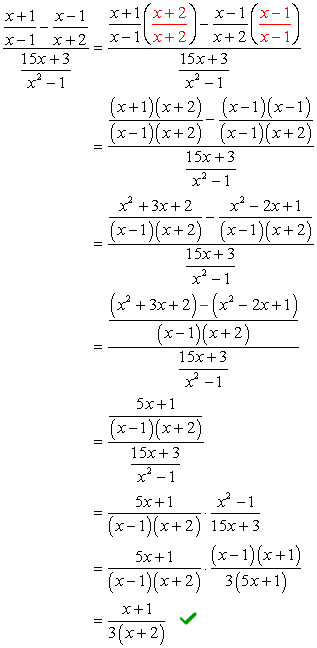
Exemple 5: Simplifier la fraction complexe ci-dessous.
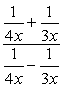
Pour résoudre ce problème, nous allons utiliser la Méthode 2 uniquement.,
observez que l’écran LCD de tous les dénominateurs est juste \color{red}12x. utilisez-le comme multiplicateur commun pour les expressions en haut et en bas.
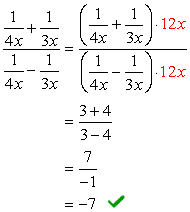
Pratique avec des Feuilles de calcul
Vous pourriez également être intéressé par:
Multiplication Complexe Fractions
Diviser des Nombres Complexes