Das reguläre Ikosaeder ist einer der fünf platonischen Körper. Es ist ein konvexes regelmäßiges Polyeder, das aus zwanzig dreieckigen Flächen besteht, wobei sich fünf an jedem der zwölf Eckpunkte treffen. Es hat 30 Kanten und 12 Eckpunkten. Seine duale Polyeder ist das Dodekaeder.,
Abmessungen
Wenn die Kantenlänge eines regulären Ikosaeders
und der Radius einer beschrifteten Kugel (Tangente zu jeder der Gesichter des Ikosaeders) ist
während der Midradius, der die Mitte jeder Kante berührt,
wobei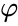

Fläche und Volumen
Die Oberfläche 
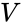

Kartesische Koordinaten
Die folgenden kartesischen Koordinaten definieren die Eckpunkte eines Ikosaeders mit Kantenlänge 2, zentriert am Ursprung:
wobei 
Die 12 Kanten eines regulären Oktaeders können im goldenen Verhältnis partitioniert werden, so dass die resultierenden Eckpunkte ein reguläres Ikosaeder definieren. Dies geschieht, indem zuerst Vektoren entlang der Kanten des Oktaeders so platziert werden, dass jede Fläche durch einen Zyklus begrenzt wird, und dann jede Kante in ähnlicher Weise entlang der Richtung ihres Vektors in das goldene Mittel unterteilt wird., Die fünf Oktaeder, die ein gegebenes Ikosaeder definieren, bilden eine reguläre polyedrische Verbindung, ebenso wie die beiden Ikosaeder, die auf diese Weise aus jedem gegebenen Oktaeder definiert werden können.
Konstruktion durch ein System von Äquiangularlinien
Die folgende Konstruktion des Icoshädrons vermeidet langwierige Berechnungen im Zahlenfeld 
Die Existenz des Ikosaeders entspricht der Existenz von sechs gleichwinkligen Linien in 
Um ein solches gleichwinkliges System zu konstruieren, beginnen wir mit der Matrix
von quadratischer Größe 


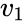
Eine einfache Berechnung ergibt 










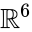



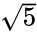

Eine zweite einfache Konstruktion des Ikosaeders verwendet die Repräsentationstheorie der alternierenden Gruppe 
Stellationen
Nach bestimmten Regeln, die im Buch Die neunundfünfzig Ikosaeder definiert sind, wurden 59 Stellationen für das reguläre Ikosaeder identifiziert. Die erste form ist das Ikosaeder selbst., Einer ist ein normaler Kepler-Poinsot-Feststoff. Drei sind regelmäßige zusammengesetzte Polyeder.
| Die Flächen des Ikosaeders erstreckten sich nach außen, wenn sich Ebenen schneiden, und definierten Regionen im Raum, wie in diesem Stellationsdiagramm der Schnittpunkte in einem einzigen Bild gezeigt flugzeug., |
|||||
Geometric relations
| Icosahedron as a snub tetrahedron., |
Icosahedron as an alternated truncated octahedron. |
There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Diese sind invariant unter den gleichen Rotationen wie das Tetraeder und sind etwas analog zu dem Snub Cube und Snub Dodekaeder, einschließlich einiger Formen, die chiral und einige mit Th-Symmetrie sind, d.h. haben verschiedene Symmetrieebenen aus dem Tetraeder. Das Ikosaeder hat eine große Anzahl von Stellationen, darunter eines der Kepler-Poinsot-Polyeder und einige der regulären Verbindungen, die hier diskutiert werden könnten.
Das Ikosaeder ist unter den platonischen Festkörpern einzigartig, da es einen diedrischen Winkel von nicht weniger als 120°besitzt. Seine dieder-Winkel ist ungefähr 138.19°.,weniger als 120° und kann nicht als die Flächen eines konvexen regulären Polyeders verwendet werden Da eine solche Konstruktion nicht die Anforderung erfüllen würde, dass mindestens drei Flächen an einem Scheitelpunkt übereinstimmen und einen positiven Defekt für die dreidimensionale Faltung hinterlassen, können Icosaeder nicht als Zellen eines konvexen regulären Polychorons verwendet werden, da in ähnlicher Weise mindestens drei Zellen an einer Kante übereinstimmen und einen positiven Defekt für die Faltung in vier Dimensionen hinterlassen müssen (im Allgemeinen für ein konvexes Polytop in 
Ein Ikosaeder kann auch als gyroelongiertes fünfeckiges Bipyramid bezeichnet werden., Es kann in eine gyroelongierte fünfeckige Pyramide und eine fünfeckige Pyramide oder in einen fünfeckigen Antiprismus und zwei gleiche fünfeckige Pyramiden zerlegt werden.
Das Ikosaeder kann auch als Snubtetraeder bezeichnet werden, da die Snubifikation eines regulären Tetraeders ein reguläres Ikosaeder ergibt., Alternativ kann man unter Verwendung der Nomenklatur für Snub-Polyeder, die sich auf einen Snub-Würfel als Snub-Cuboctaeder (Cuboctaeder = rektifizierter Würfel) und ein Snub-Dodekaeder als Snub-Icosidodekaeder (Icosidodekaeder = rektifiziertes Dodekaeder) bezieht, das Icosaeder das Snub-Oktaeder nennen (Oktaeder = rektifiziertes Tetraeder).
Ein rektifiziertes Ikosaeder bildet ein Ikosidodekaeder.
Ikosaeder vs Dodekaeder
Wenn ein Ikosaeder in eine Kugel eingeschrieben ist, nimmt es weniger des Volumens der Kugel ein (60,54%) als ein Dodekaeder, das in derselben Kugel eingeschrieben ist (66,49%).,
Da es sich um Duale handelt, ist es auch möglich, eine in die andere umzuwandeln (siehe unten).,
| Icosahedron |
Truncated icosahedron |
Icosidodecahedron |
Truncated dodecahedron |
Dodecahedron |
Uses and natural forms
|
Elektronenmikrograph des Herpes-simplex-Virus. |
Viele Viren, z.B. herpes-virus, haben die Form eines ikosaeders. Virale Strukturen bestehen aus wiederholten identischen Proteinuntereinheiten und das Ikosaeder ist die einfachste Form, um diese Untereinheiten zu montieren. Ein normales Polyeder wird verwendet, weil es aus einer einzigen Grundeinheit aufgebaut und immer wieder verwendet werden kann; Dies spart Platz im viralen Genom., |
In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.
|
Twenty-sided die., |
In einigen Rollenspielen wird der zwanzigseitige Würfel (kurz d20) verwendet, um den Erfolg oder Misserfolg einer Aktion zu bestimmen. Dieser Würfel hat die Form eines regulären Ikosaeders. Es kann zweimal von „0“ bis „9“ nummeriert werden (in welcher Form es normalerweise als zehnseitiger Würfel oder d10 dient), aber die meisten modernen Versionen sind von „1“ bis „20“gekennzeichnet. Sehen d20-System., |








