Questa sezione esamina il Teorema binomiale e il Triangolo di Pascals.
il Triangolo di Pascal
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Si dovrebbe notare che i coefficienti di (i numeri prima) a e b sono:
1 1
1 2 1
1 3 3 1
Se si continua l’espansione delle parentesi per potenze superiori, si dovrebbe trovare che la sequenza continua:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
ecc
Questa sequenza è conosciuto come il triangolo di Pascal., Ciascuno dei numeri si trova sommando i due numeri direttamente sopra di esso.
Quindi il 20 nell’ultima riga viene trovato sommando 10 e 10. Ciascuno dei 10s nella riga sopra si trovano sommando un 6 e un 4.
Quindi è possibile espandere (a + b) a qualsiasi potenza di numeri interi conoscendo il triangolo di Pascal.
Esempio
Trova (3 + x)3
La potenza a cui stiamo espandendo la parentesi è 3, quindi guardiamo la terza riga del triangolo di Pascal, che è 1 3 3 1.,
Quindi la risposta è: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(stiamo sostituendo a per 3 e b per x nell’espansione di (a + b)3 sopra)
Generalmente
È, ovviamente, spesso poco pratico scrivere il triangolo di Pascal ogni volta, quando tutto ciò che dobbiamo sapere sono le voci sull’ennesima riga. Chiaramente, il primo numero sull’ennesima riga è 1. Il secondo numero è n. Il terzo numero è:
n (n – 1) .
1 × 2
In generale, il numero rth nella riga nth è:
n! (che è nCr sulla calcolatrice)
r! (n-r)!
dove n!, significa “n fattoriale” ed è uguale a n × (n-1) × … × 2 × 1
nCr è anche spesso scritto come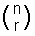 
e si pronuncia”n choose r”.
Il Teorema Binomiale
Il Teorema Binomiale stati che, dove n è un numero intero positivo:
-
(a + b)n = an + (nC1)an-1b + (nC2)un-2b2 + … + (nCn-1)abn-1 + bn
Esempio
Espandi (4 + 2x)6 in ordine crescente di potenze di x fino al termine x3
Questo significa usare il teorema Binomiale per espandere i termini in parentesi, ma solo andare più in alto x3.,
Quindi, per trovare la risposta sostituiamo 4 per il teorema Binomiale e 2x per b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Il Teorema Binomiale per (1 + x)n
La precedente versione del teorema binomiale funziona solo se n è un numero intero positivo., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
FORNENDO| x/< 1
Nota che mentre la serie precedente si ferma, questa continua per sempre.
Esempio
Trovare l’espansione di (5x + 2)1/2
Abbiamo bisogno di trasformare questo modo sembra che (1 + x)1/2, quindi, consente di stipulare un fattore 2:
(5x + 2)1/2 = (2)1/2
Ora, dove abbiamo ‘x’ nella formula sopra riportata, abbiamo bisogno di 5x/2 e, se abbiamo n, abbiamo bisogno di½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Ricordate che questo è valido solo se -1 < 5x/2 < 1, in altre parole, -2/5 < x < 2/5
l’Utilizzo Parziale Frazioni
Siamo in grado di espandere espressioni più complicate, ora, utilizzando il metodo delle frazioni parziali, ove appropriato.
Esempio