
Leonardo von Pisa (Fibonacci) (c. 1170-1250)
Der Italiener Leonardo von Pisa aus dem 13. Über sein Leben ist wenig bekannt, außer dass er der Sohn eines Zollbeamten war und als Kind mit seinem Vater durch Nordafrika reiste, wo er etwas über arabische Mathematik lernte., Nach seiner Rückkehr nach Italien half er, dieses Wissen in ganz Europa zu verbreiten, und setzte so eine Verjüngung der europäischen Mathematik in Gang, die während des Dunklen Zeitalters jahrhundertelang weitgehend ruhte.
Insbesondere schrieb er 1202 ein äußerst einflussreiches Buch mit dem Titel „Liber Abaci“ („Buch der Berechnung“), in dem er die Verwendung des hinduistisch-arabischen Zahlensystems förderte und dessen viele Vorteile für Kaufleute und Mathematiker gleichermaßen beschrieb das ungeschickte System der damals in Europa verwendeten römischen Ziffern., Trotz seiner offensichtlichen Vorteile war die Aufnahme des Systems in Europa langsam (dies war schließlich während der Kreuzzüge gegen den Islam, einer Zeit, in der alles Arabische mit großem Argwohn betrachtet wurde), und arabische Ziffern wurden sogar in der Stadt Florenz im Jahr 1299 unter dem Vorwand verboten, dass sie leichter zu fälschen waren als römische Ziffern. Der gesunde Menschenverstand setzte sich jedoch schließlich durch und das neue System wurde bis zum 15., Die horizontale Balkennotation für Brüche wurde auch zuerst in dieser Arbeit verwendet (obwohl sie der arabischen Praxis folgte, den Bruch links von der Ganzzahl zu platzieren).
Fibonacci-Sequenz

Die Entdeckung der berühmten Fibonacci-Sequenz
Fibonacci ist jedoch am besten bekannt für seine Einführung einer bestimmten Zahlenfolge in Europa, die seitdem als Fibonacci-Zahlen oder die Fibonacci-Sequenz bekannt ist., Er entdeckte die Sequenz – die erste in Europa bekannte rekursive Zahlenfolge -, während er ein praktisches Problem in der „Liber Abaci“ betrachtete, bei dem eine hypothetische Population von Kaninchen auf der Grundlage idealisierter Annahmen wuchs. Er stellte fest, dass nach jeder monatlichen Generation die Anzahl der Kaninchenpaare von 1 auf 2 auf 3 auf 5 auf 8 auf 13 usw. anstieg, und identifizierte, wie die Sequenz fortschreitete, indem die beiden vorherigen Terme hinzugefügt wurden (mathematisch gesehen Fn = Fn-1 + Fn-2), eine Sequenz, die sich theoretisch auf unbestimmte Zeit erstrecken könnte.,
Die Sequenz, die eigentlich seit dem 6.Jahrhundert indischen Mathematikern bekannt war, hat viele interessante mathematische Eigenschaften, und viele der Implikationen und Beziehungen der Sequenz wurden erst einige Jahrhunderte nach Fibonaccis Tod entdeckt., Zum Beispiel regeneriert sich die Sequenz auf überraschende Weise: Jede dritte F-Zahl ist durch 2 teilbar (F3 = 2), jede vierte F-Zahl ist durch 3 teilbar (F4 = 3), jede fünfte F-Zahl ist durch 5 teilbar (F5 = 5), jede sechste F-Zahl ist durch 8 teilbar (F6 = 8), jede siebte F-Zahl ist durch 13 teilbar (F7 = 13) usw., Es wurde auch festgestellt, dass die Zahlen der Sequenz in der Natur allgegenwärtig sind: Unter anderem haben viele Arten von Blütenpflanzen eine Anzahl von Blütenblättern in der Fibonacci-Sequenz; Die spiralförmigen Ananasanordnungen treten in 5s und 8s auf, die von Pinecones in 8s und 13s und die Samen von Sonnenblumenköpfen in 21s, 34s, 55s oder sogar höher in der Sequenz; usw.,
Das Goldene Verhältnis φ
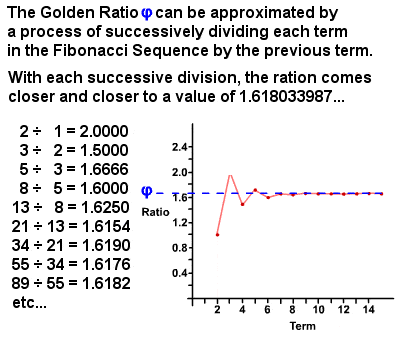
Das Goldene Verhältnis φ kann aus der Fibonacci-Sequenz abgeleitet werden
In den 1750er Jahren stellte Robert Simson fest, dass sich das Verhältnis jedes Terms in der Fibonacci-Sequenz zum vorherigen Term mit immer größerer Genauigkeit nähert, je höher die Terme sind, ein Verhältnis von ungefähr 1 : 1,6180339887 (es ist tatsächlich eine irrationale Zahl, (1 + √5)⁄2, das seitdem auf Tausende von Dezimalstellen berechnet wurde)., Dieser Wert wird als Goldener Schnitt bezeichnet, der auch als Goldener Mittelwert, Goldener Schnitt, Göttlicher Anteil usw. bezeichnet wird und normalerweise mit dem griechischen Buchstaben phi φ (oder manchmal mit dem Großbuchstaben Phi Φ) bezeichnet wird. Im Wesentlichen sind zwei Größen im Goldenen Verhältnis, wenn das Verhältnis der Summe der Mengen zur größeren Menge gleich dem Verhältnis der größeren Menge zur kleineren ist. Das Goldene Verhältnis selbst hat viele einzigartige Eigenschaften, wie 1⁄φ = φ – 1 (0,618…) und φ2 = φ + 1 (2,618…), und es gibt unzählige Beispiele dafür sowohl in der Natur als auch in der menschlichen Welt.,
Ein Rechteck mit Seiten im Verhältnis 1: φ ist als Goldenes Rechteck bekannt, und viele Künstler und Architekten im Laufe der Geschichte (aus dem alten Ägypten und Griechenland, aber besonders beliebt in der Renaissancekunst von Leonardo da Vinci und seinen Zeitgenossen) haben ihre Werke ungefähr proportioniert mit dem Goldenen Verhältnis und Goldenen Rechtecken, die weithin als von Natur aus ästhetisch ansprechend angesehen werden. Ein Bogen, der gegenüberliegende Punkte immer kleinerer verschachtelter goldener Rechtecke verbindet, bildet eine logarithmische Spirale, die als Goldene Spirale bekannt ist., Das Goldene Verhältnis und die Goldene Spirale finden sich auch in einer überraschenden Anzahl von Fällen in der Natur, von Muscheln über Blumen über Tierhörner bis hin zu menschlichen Körpern, Sturmsystemen bis hin zu vollständigen Galaxien.,
Es sollte jedoch daran erinnert werden, dass die Fibonacci – Sequenz eigentlich nur ein sehr untergeordnetes Element in „Liber Abaci“ war – tatsächlich erhielt die Sequenz erst 1877 Fibonaccis Namen, als Eduouard Lucas beschloss, ihm Tribut zu zollen, indem er die Serie nach ihm benannte-und dass Fibonacci selbst nicht dafür verantwortlich war, irgendwelche der interessanten mathematischen Eigenschaften der Sequenz, ihre Beziehung zum Goldenen Mittel und Goldenen Rechtecken und Spiralen usw. zu identifizieren.,
Gittermultiplikation
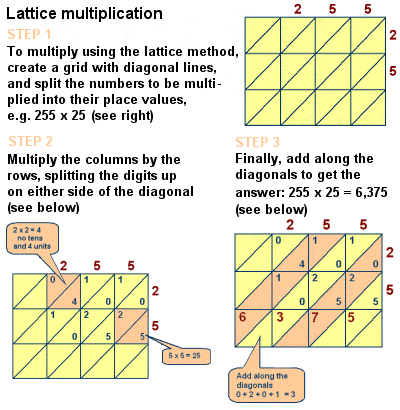
Fibonacci führte die Gittermultiplikation nach Europa ein
Der Einfluss des Buches auf die mittelalterliche Mathematik ist jedoch nicht zu leugnen, und es enthält auch Diskussionen über eine Reihe anderer mathematischer Probleme wie den chinesischen Restsatz, perfekte Zahlen und Primzahlen, Formeln für arithmetische Reihen und für quadratische Pyramidenzahlen, euklidische geometrische Beweise, und eine Studie von gleichzeitigen linearen Gleichungen entlang der Linien von Diophantus und Al-Karaji., Er beschrieb auch die Gitter – (oder Sieb -) Multiplikationsmethode zum Multiplizieren großer Zahlen, eine Methode, die ursprünglich von islamischen Mathematikern wie Al – Khwarizmi entwickelt wurde und algorithmisch der langen Multiplikation entspricht.
Weder war“ Liber Abaci “ Fibonaccis einziges Buch, obwohl es sein wichtigstes war., Sein „Liber Quadratorum“ („Das Buch der Quadrate“) ist beispielsweise ein Buch über Algebra, das 1225 veröffentlicht wurde und in dem eine Aussage über die heutige Identität von Fibonacci erscheint – manchmal auch als Brahmaguptas Identität bekannt nach dem viel früheren indischen Mathematiker, der ebenfalls zu den gleichen Schlussfolgerungen kam–, dass das Produkt von zwei Summen von zwei Quadraten selbst eine Summe von zwei Quadraten ist, z. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |