Lernergebnisse
- Machen Sie sich mit der Geschichte der Positionszahlensysteme vertraut
- Identifizieren Sie Basen, die historisch in Zahlensystemen verwendet wurden
- Zahlen zwischen Basen konvertieren
- Verwenden Sie zwei verschiedene Methoden zum Konvertieren von Zahlen zwischen Basen
Hintergrund
Wie Sie sich vorstellen können, ein Basissystem ist ein wichtiger Schritt, um den Zählprozess effizienter zu machen., Unser eigenes Base-Ten-System entstand wahrscheinlich aus der Tatsache, dass wir 10 Finger (einschließlich Daumen) an zwei Händen haben. Dies ist eine Natürliche Entwicklung. Andere Zivilisationen hatten jedoch eine Vielzahl anderer Basen als zehn. Zum Beispiel verwendeten die Eingeborenen von Queensland ein Basis-Zwei-System und zählten wie folgt: „eins, zwei, zwei und eins, zwei zwei, viel.“Einige moderne südamerikanische Stämme haben ein Base-Five-System, das auf diese Weise zählt:“ eins, zwei, drei, vier, Hand, Hand und eins, Hand und zwei “ und so weiter. Die Babylonier verwendeten ein Base-Sixty (sexigesimal) System., In diesem Kapitel schließen wir mit einem spezifischen Beispiel einer Zivilisation, die tatsächlich ein anderes Basissystem als 10 verwendet.
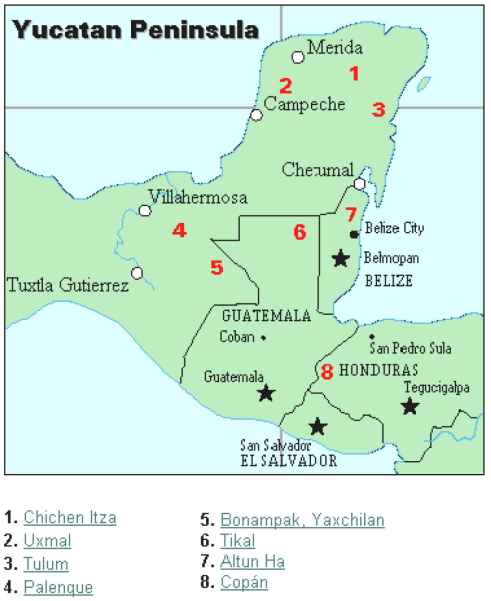 Die Maya-Zivilisation ist im Allgemeinen von 1500 v. Chr. Die Halbinsel Yucatan (siehe Abbildung 16) in Mexiko war Schauplatz der Entwicklung einer der fortschrittlichsten Zivilisationen der Antike. Die Mayas hatten ein ausgeklügeltes Ritualsystem, das von einer Priesterklasse beaufsichtigt wurde. Diese Priesterklasse entwickelte eine Philosophie mit der Zeit als göttlich und ewig., Der Kalender und die damit verbundenen Berechnungen waren daher für das rituelle Leben der Priesterklasse und damit des Maya-Volkes sehr wichtig. Tatsächlich stammt vieles, was wir über diese Kultur wissen, aus ihren Kalenderaufzeichnungen und Astronomiedaten. Eine weitere wichtige Informationsquelle über die Mayas sind die Schriften von Pater Diego de Landa, der 1549 als Missionar nach Mexiko ging.
Die Maya-Zivilisation ist im Allgemeinen von 1500 v. Chr. Die Halbinsel Yucatan (siehe Abbildung 16) in Mexiko war Schauplatz der Entwicklung einer der fortschrittlichsten Zivilisationen der Antike. Die Mayas hatten ein ausgeklügeltes Ritualsystem, das von einer Priesterklasse beaufsichtigt wurde. Diese Priesterklasse entwickelte eine Philosophie mit der Zeit als göttlich und ewig., Der Kalender und die damit verbundenen Berechnungen waren daher für das rituelle Leben der Priesterklasse und damit des Maya-Volkes sehr wichtig. Tatsächlich stammt vieles, was wir über diese Kultur wissen, aus ihren Kalenderaufzeichnungen und Astronomiedaten. Eine weitere wichtige Informationsquelle über die Mayas sind die Schriften von Pater Diego de Landa, der 1549 als Missionar nach Mexiko ging.
 Es gab zwei von den Mayas entwickelte Zahlensysteme—eines für das gemeine Volk und eines für die Priester., Diese beiden Systeme verwendeten nicht nur unterschiedliche Symbole, sondern auch unterschiedliche Basissysteme. Für die Priester wurde das Zahlensystem durch Ritual geregelt. Die Tage des Jahres galten als Götter, daher waren die formalen Symbole für die Tage verzierte Köpfe, wie die Probe links Da der Grundkalender auf 360 Tagen basierte, verwendete das Priesternummernsystem ein gemischtes Basissystem mit Vielfachen von 20 und 360. Dies sorgt für ein verwirrendes System, dessen Details wir überspringen werden.,/td>
Es gab zwei von den Mayas entwickelte Zahlensysteme—eines für das gemeine Volk und eines für die Priester., Diese beiden Systeme verwendeten nicht nur unterschiedliche Symbole, sondern auch unterschiedliche Basissysteme. Für die Priester wurde das Zahlensystem durch Ritual geregelt. Die Tage des Jahres galten als Götter, daher waren die formalen Symbole für die Tage verzierte Köpfe, wie die Probe links Da der Grundkalender auf 360 Tagen basierte, verwendete das Priesternummernsystem ein gemischtes Basissystem mit Vielfachen von 20 und 360. Dies sorgt für ein verwirrendes System, dessen Details wir überspringen werden.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the „common” people, which used a more consistent base system., Wie bereits erwähnt, verwendeten die Mayas ein Base-20-System, das als „Vigesimal“ – System bezeichnet wird. Wie unser System ist es positionell, was bedeutet, dass die Position eines numerischen Symbols seinen Ortswert angibt. In der folgenden Tabelle sehen Sie den Ortswert im vertikalen Format.
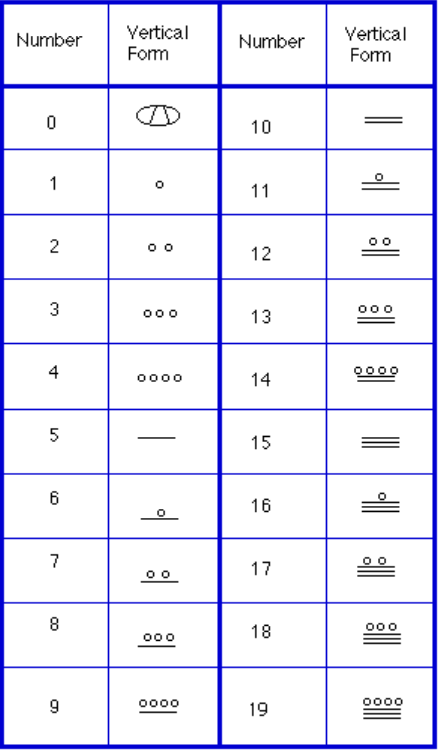
Um Zahlen aufzuschreiben, wurden in diesem System nur drei Symbole benötigt. Ein horizontaler Balken repräsentiert die Menge 5, ein Punkt repräsentiert die Menge 1 und ein spezielles Symbol (gedacht als Schale) repräsentiert Null., Das Maya-System war möglicherweise das erste, das Null als Platzhalter/Zahl verwendete. Die ersten 20 Zahlen sind in der Tabelle rechts dargestellt.
Im Gegensatz zu unserem System, bei dem der Platz rechts beginnt und sich dann nach links bewegt, platzieren die Maya-Systeme die auf dem Boden einer vertikalen Ausrichtung und bewegen sich mit steigendem Platzwert nach oben.
Wenn Zahlen in vertikaler Form geschrieben werden, sollten niemals mehr als vier Punkte an einer einzigen Stelle vorhanden sein. Beim Schreiben von Maya-Zahlen wird jede Gruppe von fünf Punkten zu einem Balken., Außerdem sollte es niemals mehr als drei Balken an einer einzigen Stelle geben…vier Balken würden an der nächsten Stelle nach oben in einen Punkt umgewandelt. Es ist das gleiche wie 10, das an der nächsten Stelle in eine 1 umgewandelt wird, wenn wir während der Addition tragen.
Beispiel
Was ist der Wert dieser Zahl, die in vertikaler Form angezeigt wird?
Beispiel
Was ist der Wert der folgenden Maya-Zahl?,
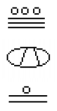
Versuchen Sie es
Konvertieren Sie die Maya-Zahl unten in Basis 10.,

Beispiel
Konvertieren Sie die Basis-10-Nummer 357510 in Maya-Ziffern.
Schreiben von zahlen mit Basen größer als 10
Wenn die Basis einer Zahl größer als 10 ist, trennen Sie jede „Ziffer“ mit einem Komma, um die Trennung der Ziffern löschen.
Zum Beispiel in Basis 20, um die Zahl entsprechend zu schreiben 17 × 202 + 6 × 201 + 13 × 200, wir würden 17,6,1320 schreiben.
Im folgenden Video präsentieren wir weitere Beispiele zum Schreiben von Zahlen mit Maya-Ziffern sowie zum Konvertieren von in Maya for geschriebenen Ziffern in Basis-10-Form.,
Das nächste Video zeigt weitere Beispiele für die Umwandlung von Basis 10 Zahlen in Maya-Ziffern.
Hinzufügen von Maya-Zahlen
Wenn wir Maya-Zahlen zusammenfügen, nehmen wir ein Schema an, das die Mayas wahrscheinlich nicht verwendet haben, das uns aber das Leben ein wenig erleichtert.
Beispiel
Fügen Sie in Maya die Zahlen 37 und 29 hinzu:

Versuchen Sie es
Versuchen Sie, 174 und 78 in Maya hinzuzufügen, indem Sie zuerst in Maya-Zahlen konvertieren und dann vollständig in diesem System arbeiten. Fügen Sie Base-Ten (dezimal) erst ganz am Ende hinzu, wenn Sie Ihre Arbeit überprüfen.
Im letzten video zeigen wir weitere Beispiele, wie das hinzufügen von Maya-Ziffern.,
In diesem Modul haben wir kurz die Entwicklung von Zahlen und unser Zählsystem skizziert, mit dem Schwerpunkt auf dem „kurzen“ Teil. Es gibt zahlreiche Informations – und Forschungsquellen, die viele Bücher zu diesem Thema füllen. Leider können wir nicht anfangen, alle Informationen, die da draußen sind, abzudecken.

Wir haben nur die Oberfläche der Fülle von Forschung und Informationen zerkratzt, die über die Entwicklung von Zahlen und Zählen im Laufe der Menschheitsgeschichte existiert., Wichtig ist, dass das System, das wir jeden Tag verwenden, ein Produkt von Tausenden von Jahren Fortschritt und Entwicklung ist. Es repräsentiert Beiträge vieler Zivilisationen und Kulturen. Es kommt nicht vom Himmel zu uns herab, ein Geschenk der Götter. Es ist nicht die Schaffung eines Lehrbuchverlags. Es ist in der Tat so menschlich wie wir, wie der Rest der Mathematik. Hinter jedem Symbol, jeder Formel und jeder Regel steht ein menschliches Gesicht, das gefunden oder zumindest gesucht werden muss.
Darüber hinaus hoffen wir, dass Sie jetzt eine grundlegende Wertschätzung dafür haben, wie interessant und vielfältig Zahlensysteme sein können., Außerdem sind wir uns ziemlich sicher, dass Sie auch erkannt haben, dass wir unser eigenes Zahlensystem so selbstverständlich halten, dass wir uns wirklich konzentrieren und darüber nachdenken müssen, was los ist, wenn wir versuchen, uns an andere Systeme oder Basen anzupassen.







