Denne delen ser vi på Binomiske Teorem og Pascals Trekant.
Pascal ‘ s Trekant
det (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Du bør legge merke til at koeffisientene i (tallene før) a og b er:
1 1
1 2 1
1 3 3 1
Hvis du fortsetter å utvide braketter for høyere makter, ville du finne at sekvensen fortsetter:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
osv
Denne sekvensen er kjent som Pascal ‘ s trekant., Hver av tallene er funnet ved å legge sammen de to tallene rett ovenfor.
Så den 20 i den siste linjen er funnet ved å legge sammen 10 og 10. Hver av de 10-ere i linjen over er funnet ved å legge sammen 6 og 4.
Slik at det er mulig å utvide (a + b) til alle hele tall kraft av å vite Pascal»s trekant.
Eksempel
Finn (3 + x)3
Den makten som vi utvider braketten til er 3, så ser vi på den tredje linjen av Pascal ‘ s trekant, som er 1 3 3 1.,
Så svaret er: 33 + 3 × (32 × x) + 3 × (x2-x 3) + x3(vi bytter ut en av 3 og b ved x i utvidelsen av (a + b)3 ovenfor)
Vanligvis
Det er, selvfølgelig, ofte upraktisk å skrive ut Pascal»s trekant hver gang, når alt det vi trenger å vite er oppføringer på nth linje. Klart, det første nummeret på den n-te linje er 1. Det andre tallet er n. Det tredje nummeret er:
n(n – 1) .
1 × 2
generelt, rth nummer i n-te linjen er:
n! (som er nCr på din kalkulator)
– r! (n – r)!
hvor n!, betyr «n fakultet» og er lik n × (n-1) × … × 2 × 1
nCr er også ofte skrevet som 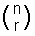 og uttales «n velg r».
og uttales «n velg r».
Den Binomiske Teorem
Den Binomiske Teorem sier at, hvor n er et positivt heltall:
-
(a + b)n = an + (nC1)en-1b + (nC2)en-2b2 + … + (nCn-1)abn-1 + bn
Eksempel
Utvid (4 + 2x)6 i stigende krefter x opp til begrepet i x3
Dette betyr bruk den Binomiske teorem å utvide vilkårene i parentes, men bare gå så høyt som x3.,
Så for å finne svaret vi erstatter 4 for en i den Binomiske teorem og 2x for b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Den Binomiske Teorem for (1 + x)n
Den forrige versjonen av den binomiske teorem fungerer bare når n er et positivt heltall., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
GI |x| < 1
Merk at mens den forrige serien stopper, dette går på for alltid.
Eksempel
Finne den utvidelse av (5x + 2)1/2
Vi trenger for å forvandle dette, så det ser ut som (1 + x)1/2, så kan du ta ut med en faktor på 2:
(5x + 2)1/2 = (2)1/2
Nå, hvor vi har en ‘x’ i ovennevnte formel, vi trenger 5x/2 og der vi har n, vi trenger½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Husk, dette er bare gyldig dersom -1 < 5x/2 < 1, med andre ord, -2/5 < x < 2/5
ved Hjelp av Delvis Fraksjoner
Vi kan utvide mer komplisert uttrykk, som nå, ved hjelp av den metoden delvis fraksjoner der det er hensiktsmessig.
Eksempel