Deze sectie bekijkt de binomiale stelling en de Pascalendriehoek.
Pascal ‘ s Triangle
so (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
merk op dat de coëfficiënten van (de getallen vóór) a en b zijn:
1 1
1 2 1
1 3 3 1
indien u de haakjes voor hogere machten blijft uitbreiden, u zou merken dat de reeks verder gaat:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
deze reeks staat bekend als de driehoek van Pascal., Elk van de getallen wordt gevonden door de twee getallen direct erboven bij elkaar op te tellen.
dus de 20 in de laatste regel wordt gevonden door 10 en 10 samen te tellen. Elk van de 10 ‘ s in de bovenstaande regel worden gevonden door een 6 en een 4 bij elkaar op te tellen.
het is dus mogelijk om (a + b) uit te breiden tot elke macht van een geheel getal door de driehoek van Pascal te kennen.
voorbeeld
Find (3 + x)3
De macht waar we de haakje naar uitbreiden is 3, dus we kijken naar de derde regel van Pascal ‘ s driehoek, die 1 3 3 1 is.,
dus het antwoord is: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(we vervangen a door 3 en b door x in de uitbreiding van (A + b) 3 hierboven)
over het algemeen
Het is natuurlijk vaak onpraktisch om elke keer de driehoek van Pascal uit te schrijven, terwijl alles wat we moeten weten de items op de nde regel zijn. Het eerste nummer op de nde lijn is duidelijk 1. Het tweede getal is n. het derde getal is:
n (n-1).
1 × 2
in het algemeen is het rth getal op de nde regel:
n! (dat is nCr op uw rekenmachine)
r! (n-r)!
waarbij n!, betekent “n faculteit” en is gelijk aan n × (n-1) × … × 2 × 1
nCr wordt ook vaak geschreven als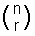 
en wordt uitgesproken als”n choose r”.
de binomiale stelling
de binomiale stelling stelt dat, waar n een positief geheel getal is:
-
(a + b)n = an + (nC1)an-1b + (nC2)an-2b2 + … + (nCn-1)abn-1 + bn
voorbeeld
Expand (4 + 2x)6 in oplopend machten van X tot aan de term in X3
Dit betekent dat de binomiale stelling gebruikt wordt om de termen tussen de haakjes uit te breiden, maar alleen tot x3 gaat.,
om het antwoord te vinden vervangen we 4 voor a in de binomiale stelling en 2x voor b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
de binomiale stelling voor (1 + x)n
de vorige versie van de binomiale stelling werkt alleen als n een positief geheel getal is., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
PROVIDING |x| < 1
merk op dat terwijl de vorige reeks stopt, deze voor altijd doorgaat.
voorbeeld
Zoek de expansie van (5x + 2)1/2
We moeten dit transformeren zodat het eruit ziet als (1 + x)1/2, dus laten we een factor van 2 nemen:
(5x + 2)1/2 = (2)1/2
nu, waar we ‘x’ in de bovenstaande formule hebben, hebben we 5x/2 nodig en waar we n hebben, hebben we ½ nodig .,
= Ö2(1 + 5x/2)1/2
= Ö2
onthoud, dit is alleen geldig als -1 < 5x/2 < 1, met andere woorden, -2/5 < x < 2/5
met behulp van partiële fracties
We kunnen nu meer gecompliceerde expressies uitbreiden met behulp van de methode van partiële fracties waar van toepassing.
voorbeeld