rozkłady
głównym problemem problemów z Deltą Diraca i podobnymi obiektami matematycznymi
jest problem różniczkowalności. Jak stwierdził Dirac w powyższym cytacie, nie wpadasz w kłopoty, jeśli użyjesz jego funkcji δ jako symbolicznej reguły dla tego, jak działa ona na inne funkcje; jednak on przechodzi do rozróżniania δ w swoich obliczeniach, i to jest miejsce, gdzie naprawdę zaczynają się problemy., Jak można wiedzieć a priori „kiedy te operacje są dopuszczalne”, skoro nie ma się nawet jednoznacznej definicji obiektów, lub co oznaczałoby ich rozróżnienie? Zobaczymy, jak te pytania prowadzą do wyprowadzania nowych i rygorystycznie zdefiniowanych obiektów matematycznych.
funkcje
rozważ, w jaki sposób zwykle określa się pochodną (lub antyderyvatywną) funkcji. W normalnych okolicznościach, z” klasycznymi ” funkcjami, masz dobrze zdefiniowaną regułę, która opisuje, jak funkcja odwzorowuje jeden zbiór liczb rzeczywistych do innego zbioru, powiedzmy f: ℝ →ℝ., Biorąc pod uwagę to i definicje całki lub pochodnej, można łatwo zbadać wartości, które te operatory dają, gdy są stosowane do funkcji. W przypadku δ nie mamy wykonalnej definicji, aby postępować zgodnie z tymi liniami. Zamiast tego, w praktyce δ jest najczęściej definiowana przez to, jak działa na innych, dobrze zdefiniowanych funkcjach (jak w (3)). Jest to kluczowy wgląd, który prowadzi do współczesnej teorii dystrybucji. Okazuje się, że poprawnym sposobem matematycznego traktowania δ i dużej klasy podobnych obiektów jest zaprzestanie prób definiowania ich w ogóle jako funkcji., Ta linia myślenia jest dobrze opisana przez Jean Dieudonne w jego recenzji (patrz):
… zaczyna się od rodziny bardzo” regularnych ” funkcji (zwykle z
w odniesieniu do własności różniczkowych), które spełniają pewne (ogólnie
całkowe) relacje, lub na których pewne operacje są możliwe; i
następnie odkrywa się, że a priori większa rodzina funkcji spełnia
te same relacje, lub może być poddawana podobnym operacjom. Wiele
pytań można wtedy naturalnie zadać: czy ta nowa rodzina naprawdę
różni się od pierwszej?, Jeśli tak, to jakie są relacje między
dwiema rodzinami i czy można podać dokładny opis nowej?
dopiero w ostatniej fazie ” prehistorii „pojawi się coś, co może być
nazywane rewolucyjnym punktem widzenia, z myślą, że
” nowa rodzina ” może składać się z obiektów innych niż funkcje.
pozostałe obiekty są funkcjami. Funkcję
można traktować jako funkcję funkcji., Ponieważ funkcja jest unikalnym odwzorowaniem z jednego zbioru liczb
do drugiego, funkcja F może być zdefiniowana jako odwzorowanie F: C →ℝ,
Gdzie C jest pewnym zbiorem funkcji. Oznacza to, że funkcja odwzorowuje funkcje liczb rzeczywistych
., Prostym przykładem funkcji tego typu jest Całka określona:

, który wyraźnie pobiera funkcję F z pewnego zestawu odpowiednio całkowalnych funkcji i mapuje ją do liczby rzeczywistej, wartości całki lub obszaru pod krzywą F(X) między A i B. jest to tylko jeden przykład., Można sobie wyobrazić nieskończoną liczbę funkcji i zbiorów funkcji; można nawet nadal uogólniać i definiować odwzorowania ze zbiorów funkcji do liczb rzeczywistych. To nie jest ani tu, ani tam. Ważne jest to, że pojęcie funkcjonalne może być używane do definiowania dystrybucji.
zestaw funkcji testowych
aby osiągnąć nasz cel, potrzebujemy jeszcze jednej definicji. Sprowadza się to do określenia zbioru C funkcji, z których dystrybucje będą mapować funkcje do liczb rzeczywistych., Funkcje są często zbierane w zbiorach, które określają stopień ich ciągłości, różniczkowalności i ciągłości ich pochodnych. Mówimy, że funkcja f jest w zbiorze C⁰ (napisz f ∈ C⁰), jeśli jest ciągła na całej linii rzeczywistej w tym sensie, że granica we wszystkich punktach jest taka sama, gdy jest brana z lewej lub prawej strony; niekoniecznie jest różniczkowalna. Mówimy, że f ∈ C1, jeśli jego pochodna istnieje i jest ciągła, tj. f ' ∈ C⁰. Na przykład funkcja g (x) = / x / jest ciągła, ale nie różniczkowalna Przy x = 0; g jest w C⁰, ale nie w C1., Możemy to uogólnić i powiedzieć, że Cⁿ jest zbiorem funkcji, które dla funkcji ciągłych mają swoje pierwsze N pochodne, gdzie n jest liczbą całkowitą.
gdy n staje się większe, zbiory stają się w pewnym sensie „mniejsze”; zawsze można znaleźć funkcje (nieskończenie wiele!), które są w Cⁿ, ale nie cⁿ ⁺ 1. Te „przestrzenie ciągłości” tworzą więc ciąg zagnieżdżonych podzbiorów, jak przedstawiono poniżej.

na dole tej nieskończonej sekwencji zestawów funkcji znajdujemy zestaw
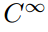
który jest oczywiście zbiorem wszystkich funkcji, które mają nieskończenie wiele ciągłych pochodnych. Wiele znanych i przyjaznych funkcji jest w tej drugiej klasie (np. sin( x); cos (x); eˣ; wszystkie wielomiany)., Funkcje te nazywane są „gładkie” lub „dobrze wychowane”, ponieważ można wykonać na nich operację różnicowania tyle razy, ile się podoba bez opieki. Ale chociaż ten zestaw z pewnością ma nieskończenie wiele członów, są one rzadkie w tym sensie, że większość funkcji nie jest tak dobrze zachowana.
zbiór, który nadaje się do definicji dystrybucji jest jeszcze mniejszy
niż ten. Wymaga to dodatkowego kryterium: że funkcje mają zwartą obsługę. Ten termin techniczny oznacza po prostu, że funkcja ma wartości niezerowe w skończonej domenie i jest równomiernie zerowa poza tym., Dlatego używamy notacji
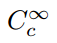
aby określić zbiór nieskończenie ciągłych funkcji różnicowalnych z kompaktową obsługą i wywołać takie funkcje funkcje testowe. W celu zdefiniowania klasy funkcji używających tego zbioru jako domeny, powinniśmy być pewni, że rzeczywiście istnieją członkowie tego zbioru., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

definicja
od tego momentu definicja rozkładu jest prosta. Rozkład jest funkcją liniową
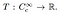
oznacza to, że jest to odwzorowanie z zestawu funkcji testowych na liczbę rzeczywistą. Analogicznie do tego, jak określona funkcja działa na liczbę wejściową i produkuje wyjście, określone rozkłady są definiowane przez sposób przekształcania funkcji testowych w liczby., Podział funkcji testowej φ może być zapisany jako T (φ) lub powszechnie jako〈T, φ〉.
teraz widać, dlaczego dystrybucje nazywane są funkcjami uogólnionymi. Dla dowolnej
klasycznej funkcji, dla której Całka

jest dobrze zdefiniowany,istnieje odpowiedni rozkład f taki, że 〈F, φ〉daje wartość tej całki., Istnieją jednak również dystrybucje, które nie odpowiadają funkcjom klasycznym; dystrybucje są bardziej ogólne. Jak już powinno być jasne, kanonicznym przykładem rozkładu, który nie odpowiada funkcji klasycznej jest Diraca δ., Dlatego wreszcie doszliśmy do w pełni rygorystycznej definicji δ jako rozkładu takiego, że

uogólniona lub „słaba” pochodna
rozkład δ jest tylko jednym z nieskończenie wielu rozkładów, które nie odpowiadają
funkcjom klasycznym. Możemy uzyskać ich więcej, różnicując δ w sensie rozkładów., Ale w jaki sposób pojęcie rozkładu
rozwiązuje problem różnicowania, jak zostało to omówione wcześniej? Musimy tylko uogólnić pojęcie różnicowania, aby zastosować je do dystrybucji.
rozważmy funkcję f ∈ C1, tak aby była stale różniczkowalna. Obliczanie za pomocą integracji przez części, widzimy, że

termin w nawiasach znika, ponieważ φ, jako funkcja testowa, ma zwartą obsługę., To uogólnia się na dystrybucję, powiedzmy F', odpowiadającą funkcji f':

div>
To obliczenie uogólnia dość łatwo dystrybucje, które nie odpowiadają klasycznej funkcji f., W ten sposób możemy zdefiniować pochodną T' T w sensie dystrybucji:

jest to również czasami określane jako słaba pochodna, ponieważ rozszerza pochodne na funkcje, które normalnie nie byłyby różnicowalne. To uogólnia się jeszcze bardziej, do pochodnych wyższego rzędu., Możemy zdefiniować n-tą pochodną rozkładu T jako T ⁽ ⁿ ⁾, gdzie ta druga jest rozkładem takim, że

tutaj,
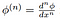
iv id=”5c0413871b”
jest klasyczną pochodną funkcji testowej, która jest zapewniona
istnieć dzięki samej definicji funkcji testowych!, Wynika z tego, że wszystkie dystrybucje są nieskończenie różniczkowalne(w sensie dystrybucji).
to całkowicie usuwa zmagania, które Diraca i inni napotykali podczas różnicowania funkcji δ. Przez to, co tutaj zdefiniowaliśmy, pochodna δ Po prostu przesiąka dla wartości innej pochodnej funkcji na zero., Formalnie,

zapewnia to rygorystyczne ramy matematyczne dla pochodnych δ, które pojawiły się w literaturze na długo przed powstaniem tej teorii.
istnieje wiele innych operacji, które mają zastosowanie do funkcji, które zostały uogólnione na dystrybucje. Można je dodawać i odejmować, konwertować i przekształcać za pomocą przekształceń Laplace ' a i Fouriera., Niemożliwe jest jednak zdefiniowanie mnożenia rozkładów w sposób zachowujący algebrę, która ma zastosowanie do funkcji klasycznych (twierdzenie Schwartza o niemożności).