Icosahedron (Polski)

zwykły icosahedron jest jedną z pięciu brył platonicznych. Jest to wypukły regularny polihedron złożony z dwudziestu trójkątnych twarzy, z pięcioma spotkaniami na każdym z dwunastu wierzchołków. Ma 30 krawędzi i 12 wierzchołków. Jego podwójny wielościan to dwunastościan.,

wymiary

jeśli długość krawędzi zwykłego icosahedronu wynosi , promień ograniczonej sfery (takiej, która dotyka icosahedronu na wszystkich wierzchołkach) wynosi

i promień wpisanej sfery (stycznej do każdego z icosahedronów jest to

podczas gdy midradius, który dotyka środka każdej krawędzi, jest

gdzie 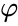(nazywany również ) to złoty stosunek.,

powierzchnia i objętość

powierzchnia I objętość zwykłego ikozahedronu o długości krawędzi to:

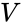
współrzędne kartezjańskie

następujące współrzędne kartezjańskie definiują wierzchołki ikozahedronu o długości krawędzi 2, wyśrodkowane na początku:

gdzie jest złotym współczynnikiem (również zapisanym τ)., Zauważ, że te wierzchołki tworzą pięć zestawów trzech wzajemnie wyśrodkowanych, wzajemnie ortogonalnych złotych prostokątów.

12 KRAWĘDZI ośmiościanu regularnego można podzielić na Złote proporcje, tak aby powstałe wierzchołki definiowały regularny ośmiościan. Odbywa się to najpierw przez umieszczenie wektorów wzdłuż krawędzi oktaedronu tak, że każda twarz jest ograniczona cyklem, a następnie podobnie dzieląc każdą krawędź na złotą średnią wzdłuż kierunku jego wektora., Pięć oktaedrów definiujących dany Oktaedr tworzy regularny związek wielościenny, podobnie jak dwie oktaedry, które można zdefiniować w ten sposób z dowolnego danego oktaedru.

Budowa za pomocą systemu linii równokątnych

następująca konstrukcja icoshaedronu pozwala uniknąć żmudnych obliczeń w polu liczbowym niezbędnych w bardziej elementarnych podejściach.

istnienie icosahedronu jest równoznaczne z istnieniem sześciu linii równoramiennych w ., W rzeczywistości przecięcie takiego układu linii równorzędnych ze sferą euklidesową skupioną na ich wspólnym przecięciu daje dwanaście wierzchołków regularnego ikozahedronu, co można łatwo sprawdzić. Z drugiej strony, zakładając istnienie regularnego ikozaedronu, linie zdefiniowane przez jego sześć par przeciwległych wierzchołków tworzą układ równokątny.

aby skonstruować taki układ równokątny, zaczynamy od macierzy

o rozmiarze kwadratu ., (Mnemonic: macierz koduje kąty, ostre dla dodatniego wejścia, rozwarte inaczej, między pięcioma cyklicznie kolejnymi wierzchołkami przylegającymi do pierwszego wierzchołka ikozahedronu wyśrodkowanego na początku.)

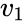
proste obliczenia dają . Oznacza to, że ma wartości własne, obie z wielokrotnością 3, ponieważ jest symetryczne i ma ślad 0., Macierz indukuje strukturę euklidesową na przestrzeni ilorazowej która jest izomorficzna do od jądra z ma wymiar 3. Obraz pod projekcją sześciu osi współrzędnych w tworzy w ten sposób układ sześciu linii równorzędnych w przecinających się parami pod wspólnym kątem ostrym ., Rzut ortogonalny na -eigenspace daje w ten sposób dwanaście wierzchołków icosahedronu.

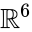
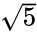
druga prosta konstrukcja icosahedronu wykorzystuje teorię reprezentacji grupy przemiennej działającą przez bezpośrednie izometrie na icosahedronie.

Stellacje

zgodnie ze szczegółowymi zasadami określonymi w książce the fifty nine icosahedra zidentyfikowano 59 stellacji dla zwykłego icosahedronu. Pierwszą formą jest sam ikosahedron., Jeden z nich to zwykła bryła Keplera-Poinsota. Trzy to zwykłe wielościany złożone.

21 of 59 stellations

twarze icosahedron extended na zewnątrz, jak płaszczyzny przecinają, definiowanie regionów w przestrzeni, jak pokazano na tym diagramie stellation przecięć w jednej płaszczyźnie.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Są one niezmienne pod tymi samymi obrotami, co czworościan, i są nieco analogiczne do sześcianu i dwunastościanu, w tym niektóre formy, które są chiralne i niektóre z symetrią TH, tj. mają różne płaszczyzny symetrii od czworościanu. Ikosahedron ma dużą liczbę stellacji, w tym jedną z wielościanów Kepler-Poinsot i niektóre związki regularne, które można tutaj omówić.

icosahedron jest unikalny wśród ciał stałych platonicznych, ponieważ ma kąt dwudzielny nie mniejszy niż 120°. Jego kąt nachylenia wynosi około 138,19°.,ikozahedra nie może być używana jako komórki wypukłego polichoronu regularnego, ponieważ podobnie, co najmniej trzy komórki muszą się spotkać na krawędzi i pozostawić dodatnią wadę do składania w czterech wymiarach (ogólnie dla wypukłego politopu w wymiary, w wymiary, w wymiary, w wymiary, w co najmniej trzy aspekty muszą spotkać się na szczycie i pozostawić dodatnią wadę do złożenia w n-przestrzeni)., Jednak w połączeniu z odpowiednimi komórkami o mniejszych kątach dwudzielnych ikosahedra może być używana jako komórki w półregularnej polichorze (na przykład snub 24-cell), podobnie jak sześciokąty mogą być używane jako twarze w półregularnej polihedrze (na przykład okrojony ikosahedron). W końcu, non-convex polytopes nie niosą te same ścisłe wymagania co convex polytopes, i icosahedra są rzeczywiście komórki icosahedral 120-komórka, jeden z dziesięciu non-convex regularna polichora.

ikosahedron może być również nazywany gyroelongated pentagonal bipiramid., Może być rozłożony na żyroelongowaną pięciokątną piramidę i pięciokątną piramidę lub na pięciokątny antypryzm i dwie równe pięciokątne piramidy.

icosahedron może być również nazywany czworościanem snub, ponieważ snubification of a regular tetrahedron gives a regular icosahedron., Alternatywnie, używając nomenklatury dla snub polyhedra, która odnosi się do sześcianu snub jako cuboctahedron (cuboctahedron = prostowany sześcian) i dodekahedronu snub jako snub icosidodecahedron (icosidodecahedron = prostowany dodekahedron), można nazwać icosahedron ośmiościanem snub (octahedron = prostowany czworościan).

a rectified icosahedron forms a icosidodecahedron.

Ikosahedron vs dodekahedron

gdy ikosahedron jest wpisany w kulę, zajmuje mniej objętości kuli (60,54%) niż dodekahedron wpisany w tę samą kulę (66,49%).,

ponieważ są to Duale, możliwe jest przekształcenie jednego w drugi (patrz niżej).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	w niektórych grach fabularnych dwudziestostronna matryca (w skrócie d20) jest używana do określania sukcesu lub porażki danej akcji. Ta matryca ma postać zwykłego ikozahedronu. Może być ponumerowany od” 0 „do” 9 ” dwukrotnie (w tej formie zwykle służy jako matryca dziesięciostronna lub d10), ale większość współczesnych wersji jest oznaczana od „1” do „20”. Zobacz System d20.,

icosahedron to trójwymiarowa plansza do gry Icosagame, wcześniej znana jako gra ICO Crystal.

ikosahedron jest używany w grze planszowej Scattergories, aby wybrać literę alfabetu. Sześć mało używanych liter, takich jak X, Q i Z, są pomijane.

wewnątrz magicznej 8-kuli, różne odpowiedzi na pytania tak-nie są drukowane na zwykłym icosahedronie.

ikosahedron wyświetlany w formie funkcjonalnej jest widoczny w jasnym odcieniu Sol de la Flor., Rozeta uformowana przez nakładające się na siebie elementy wykazuje podobieństwo do kwiatu Frangipani.

Jeśli każda krawędź icosahedronu zostanie zastąpiona przez rezystor 1 ohm, Rezystancja między przeciwległymi wierzchołkami wynosi 0,5 oma, a pomiędzy sąsiednimi wierzchołkami 11/30 omów.

Grupa symetrii iloczynu jest izomorficzna z grupą przemienną na pięć liter. Ta nieabelowska Grupa prosta jest jedyną nietrywialną podgrupą normalną grupy symetrycznej na pięciu literach., Ponieważ Grupa Galois ogólnego równania kwintycznego jest izomorficzna z grupą symetryczną na pięciu literach, a fakt, że grupa ikosahedralna jest prosta i nieabelowa oznacza, że równania kwintyczne nie muszą mieć rozwiązania w rodnikach. Dowód twierdzenia Abela-Ruffiniego wykorzystuje ten prosty fakt, a Felix Klein napisał książkę, która wykorzystała teorię symetrii ikosahedralnych do uzyskania analitycznego rozwiązania ogólnego równania kwintycznego.,

patrz również

szablon:Wikionarypar

• okrojony icosahedron
• zwykły wielościan
• siatki geodezyjne używają iteracyjnie podzielonego icosahedronu do generowania siatek na kuli
• ikosahedron Jessena

szablon:Wikisource1911Enc

template:commonscat

• Weisstein, Eric W., „icosahedron” from MathWorld.
• papierowe modele ikosahedronu
• Polihedra mundurowa
• K. J. M., MacLean, a Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Interactive Icosahedron model-works right in your web browser
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Tulane.,Edu-to jest dyskusja na temat zabudów i dwudziestościan
• papierowe modele objętości wielościanów wiele odniesień
• origami многогранники – wszystkie modele wykonane są z origami modułowym
• wideo икосаэдрической lustro rzeźba

szablon:многогранники

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri ja rregulltsr:Икосаедарsv:Ikosaederta:wybuchł முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.