Introduction to Philosophy: Logic (Polski)

istnieje starożytny pogląd, wciąż powszechnie uznawany, że to, co czyni człowieka wyjątkowym—co odróżnia nas od „bestii polnych” – to to, że jesteśmy racjonalni. Na czym polega racjonalność? Jest to drażliwe pytanie, ale jedna z możliwych odpowiedzi brzmi mniej więcej tak: manifestujemy naszą racjonalność, angażując się w działania, które obejmują rozumowanie—roszczenie i popieranie ich uzasadnieniami, działanie zgodnie z powodami i przekonaniami, wyciąganie wniosków z dostępnych dowodów i tak dalej.,

ta czynność rozumowania może być wykonana dobrze i może być wykonana źle; może być wykonana poprawnie lub nieprawidłowo. Logika jest dyscypliną, która ma na celu odróżnienie dobrego rozumowania od złego.

dobre rozumowanie niekoniecznie jest skutecznym rozumowaniem. W rzeczywistości, jak zobaczymy w kolejnym rozdziale o błędach logicznych, złe rozumowanie jest wszechobecne i często niezwykle skuteczne—w tym sensie, że ludzie często są przez nie przekonywani. W logice standardem dobroci nie jest skuteczność w sensie perswazji, ale raczej poprawność według zasad logicznych.,

na przykład rozważ Hitlera. Przekonał cały naród, aby poszedł na różne propozycje, które były nie tylko fałszywe, ale wręcz złe. Nie zdziwisz się, gdy usłyszysz, że jeśli przyjrzysz się temu krytycznie, jego rozumowanie nie przejdzie logicznego zebrania. Argumenty Hitlera były skuteczne, ale nie logicznie poprawne. Co więcej, jego techniki perswazyjne wykraczają poza rozumowanie w sensie potwierdzania twierdzeń z przyczynami. Hitler opierał się na groźbach, manipulacjach emocjonalnych, niepopartych twierdzeniach itp. Istnieje wiele retorycznych sztuczek, które można wykorzystać, aby przekonać.,

w logice badamy zasady i techniki, które pozwalają nam odróżnić dobre, poprawne rozumowanie od złego, błędnego rozumowania.

ponieważ istnieje wiele różnych rodzajów rozumowania i metod oceny każdego z tych typów, a także różne rozbieżne poglądy na to, co stanowi prawidłowe rozumowanie, istnieje wiele podejść do logicznego przedsięwzięcia. Mówimy o logice, ale także o logice. Logika jest tylko zbiorem zasad i technik odróżniania dobrego rozumowania od złego., Logika musi sformułować precyzyjne standardy oceny rozumowania i opracować metody stosowania tych standardów do poszczególnych instancji.

podstawowe pojęcia

rozumowanie obejmuje twierdzenia lub twierdzenia—formułowanie ich i popieranie uzasadnieniami, wyciąganie ich konsekwencji. Twierdzenia to rzeczy, które twierdzimy, stwierdzamy, twierdzimy.

propozycje to rzeczy, które mogą być prawdziwe lub fałszywe. Wyrażane są za pomocą zdań deklaratywnych., Używamy takich zdań do robienia wszelkiego rodzaju twierdzeń, od rutynowych spraw faktycznych („Ziemia obraca się wokół Słońca”), przez wielkie tezy metafizyczne („rzeczywistość jest niezmiennym, bez cech, jednolitym absolutem”), po twierdzenia o moralności („jedzenie mięsa jest złe”).

ważne jest, aby odróżnić zdania w nastroju deklaratywnym, które wyrażają propozycje, od zdań w innych nastrojach, które nie. Zdania pytające, np. zadają pytania („czy pada deszcz?”), a zdania imperatywne wydają polecenia („nie pij nafty.”)., Nie ma sensu pytać, czy tego rodzaju zdania wyrażają prawdę czy fałsz, więc nie wyrażają propozycji.

rozróżniamy również propozycje od zdań, które je wyrażają, ponieważ jedna propozycja może być wyrażona przez różne zdania. „It' s raining ” i „es regnet” wyrażają propozycję, że pada; jedno zdanie robi to po angielsku, drugie po niemiecku. Również „John kocha Mary” i „Mary is loved by John” wyrażają tę samą propozycję.

podstawową jednostką rozumowania jest argument., W logice, przez „argument” nie rozumiemy niezgody, krzyczącego meczu; raczej definiujemy termin dokładnie:

Argument = zbiór propozycji, z których jedna, wniosek, jest (ma być) poparta przez inne, przesłanki.

Jeśli rozumujemy, składając twierdzenia i popierając je uzasadnieniami, to twierdzenie, które jest poparte, jest konkluzją argumentu; powody podane na jego poparcie są przesłankami argumentu., Jeśli rozumujemy wyciągając wniosek ze zbioru twierdzeń, to wnioskowanie, które wyciągamy, jest wnioskiem argumentu, a twierdzenia, z których jest wyciągnięty, są przesłankami.

w definicji umieszczamy nawias—”niby być”—aby zrobić miejsce na złe argumenty. Zły argument, bardzo z grubsza mówiąc, to taki, w którym przesłanki nie popierają wniosku; przesłanki dobrego argumentu rzeczywiście popierają wniosek.

Analiza argumentów

poniższy fragment wyraża argument:

tak samo jak ten fragment:

ostatecznym celem logiki jest ocena argumentów—odróżnienie dobra od zła. Wymaga to rozróżnień, definicji, zasad i technik, które zostaną przedstawione w kolejnych rozdziałach. Na razie skupimy się na identyfikacji i rekonstrukcji argumentów.

pierwszym zadaniem jest wyjaśnienie argumentów—jednoznaczne określenie ich przesłanek i wniosków., Czytelnym sposobem na to jest po prostu lista zdań deklaratywnych wyrażających odpowiednie propozycje, z linią oddzielającą przesłanki od wniosku, a więc:

1. McDonald ' s płaci swoim pracownikom bardzo niskie zarobki.
2. zwierzęta, które dostarczają mięsa McDonalda, są hodowane w godnych pożałowania warunkach.
3. jedzenie w McDonaldzie jest bardzo niezdrowe.
4. / \dlatego nie powinieneś jeść w McDonaldzie.

jest to Wyjaśnienie pierwszego argumentu powyżej., Aby zidentyfikować wniosek z argumentu, warto zadać sobie pytanie: „co ta osoba próbuje przekonać mnie do wiary, mówiąc te rzeczy? Jaki jest ostateczny punkt tego fragmentu?”Odpowiedź jest dość jasna w tym przypadku. Inną wskazówką co się dzieje w tym fragmencie jest słowo „ponieważ” w trzecim zdaniu. Wraz z innymi słowami, takimi jak „since” I „for”, wskazuje na obecność przesłanki. Takie słowa możemy nazwać znacznikami akomodacji. Symbol „/ ∴ „można odczytać jako skrót od” dlatego.,”Wraz z wyrażeniami takimi jak „w konsekwencji”, „w ten sposób”, „wynika to z tego” i „co oznacza, że”, „dlatego” jest wskaźnikiem, że wniosek argumentu ma nastąpić. Takie lokalizacje nazywamy znacznikami konkluzji. Taki znacznik nie występuje w pierwszym argumencie, ale widzimy jeden w drugim, który można wyjaśnić w ten sposób:

1. wszechświat jest rozległy i złożony.
2. wszechświat wykazuje zadziwiający stopień uporządkowania.
3. planety krążą wokół Słońca zgodnie z regularnymi prawami.
4. najmniejsze części zwierząt są ułożone dokładnie tak, aby służyły ich celom.,
5. taka kolejność i złożoność nie mogą powstawać przypadkowo.
6. / \dlatego wszechświat musi być wytworem twórcy ogromnej mocy i intelektu: Boga.

warto tu zwrócić uwagę na kilka punktów porównania do naszego pierwszego wyjaśnienia. Po pierwsze, jak wspomniano, zostaliśmy ostrzeżeni o zakończeniu przez słowo ” dlatego.”Po drugie, ten fragment wymagał znacznie więcej parafrazy niż pierwszy. Drugie zdanie jest pytające, a nie deklaratywne, a więc nie wyraża propozycji., Ponieważ argumenty są z definicji zbiorem propozycji, musimy ograniczyć się do zdań deklaratywnych, gdy je wyjaśniamy. Ponieważ odpowiedź na pytanie retoryczne drugiego zdania jest wyraźnie „tak”, parafrazujemy jak pokazano. Trzecie zdanie wyraża dwie propozycje, więc w naszym wyjaśnieniu rozdzielamy je; każda z nich jest przesłanką.

Więc czasami, kiedy wyjaśniamy argument, musimy wziąć to, co jest obecne w fragmencie argumentacyjnym I zmienić go nieznacznie, tak aby wszystkie zdania, które zapisujemy, wyrażały propozycje obecne w argumencie., To parafrazowanie. Innym razem musimy zrobić jeszcze więcej. Na przykład, możemy być zmuszeni do wprowadzenia propozycji, które nie są wyraźnie wymienione w fragmencie argumentacyjnym, ale są niewątpliwie używane w rozumowaniu argumentu.

istnieje greckie słowo na argumentacyjne fragmenty, które pozostawiają pewne propozycje nieutwardzone: entymemes. Oto przykład:

w tle czai się ukryta przesłanka—coś, co nie zostało powiedziane, ale co musi być prawdziwe, aby argument przeszedł. Potrzebujemy twierdzenia, które łączy przesłankę z wnioskiem-które wypełnia lukę między nimi. Coś takiego: wszechmiłujący Bóg nie pozwoliłby cierpieć niewinnym ludziom. A może: powszechne cierpienie jest niezgodne z ideą wszechmiłującego bóstwa. Przesłanka wskazuje na cierpienie, podczas gdy wniosek dotyczy Boga; te propozycje łączą te dwa twierdzenia., Pełne wyjaśnienie argumentacyjnego fragmentu sprawiłoby, że taka propozycja byłaby jednoznaczna:

1. wielu niewinnych ludzi na całym świecie cierpi.
2. wszechmiłujący Bóg nie pozwoliłby cierpieć niewinnym ludziom.
3. / \dlatego nie może być wszechmiłującego Boga.

to jest znak rodzajów milczących przesłanek, które chcemy odkryć: jeśli są fałszywe, podważają argument., Często takie przesłanki nie są sprecyzowane z jakiegoś powodu: same w sobie są kontrowersyjnymi twierdzeniami, wymagającymi dowodów na ich poparcie; więc arguer je pomija, woląc nie ugrzęznąć. Kiedy jednak je wyciągniemy, możemy wymusić bardziej solidną wymianę dialektyczną, skupiając argument na sednie sprawy. W tym przypadku, dyskusja na temat zgodności dobroci Boga i zła w świecie byłoby w porządku. Jest wiele do powiedzenia na ten temat., Filozofowie i teolodzy opracowali na przestrzeni wieków rozbudowane argumenty, aby bronić idei, że dobroć Boża i ludzkie cierpienie są w rzeczywistości zgodne.

do tej pory nasza analiza argumentów nie była szczególnie głęboka. Zauważyliśmy, jak ważne jest określenie konkluzji i wyraźne określenie przesłanek, ale nie przyjrzeliśmy się sposobom, w jaki zbiory przesłanek mogą wspierać ich wnioski. Zauważyliśmy jedynie, że zbiorowo przesłanki stanowią poparcie dla wniosków., Nie przyjrzeliśmy się, jak to robią, jakie relacje mają ze sobą. Wymaga to głębszej analizy.

często różne przesłanki wspierają wniosek—lub inną przesłankę—indywidualnie, bez pomocy innych. Rozważ ten prosty argument:

propozycje 1 i 2 popierają wniosek, propozycja 3—i czynią to niezależnie. Każda z nich daje nam powód, aby wierzyć, że wojna była niesprawiedliwa, a każda z nich jest powodem, nawet jeśli mamy przypuszczać, że druga nie była prawdziwa; jest to znak niezależnych przesłanek.

pomocne może być, zwłaszcza gdy argumenty są bardziej złożone, rysowanie diagramów przedstawiających relacje między przesłankami i wnioskami., Możemy przedstawić powyższy argument w następujący sposób:

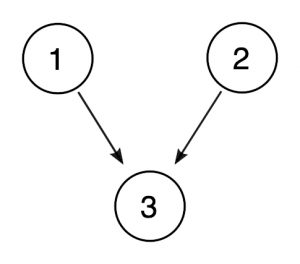
w takim diagramie zakreślone liczby reprezentują propozycje, a strzałki reprezentują relację wsparcia z jednej propozycji do drugiej. Ponieważ propozycje 1 i 2 Każda wspierają 3 niezależnie, otrzymują własne strzały.

Możliwe są inne relacje między lokalami. Czasami przesłanki wspierają wnioski tylko pośrednio, dając nam powód, by wierzyć w jakieś inne przesłanki, które są pośrednie między tymi dwoma twierdzeniami., Rozważ następujący argument:

w tym przykładzie propozycja 1 zapewnia wsparcie dla propozycji 2( Słowo” stąd ” jest wskazówką), podczas gdy propozycja 2 bezpośrednio wspiera wniosek w 3., Relacje między tymi wnioskami przedstawilibyśmy w następujący sposób:

czasami przesłanki muszą współpracować, aby zapewnić wsparcie dla innego roszczenia, nie dlatego, że jedno z nich daje powód do wiary drugiemu, ale dlatego, że żadne z nich nie zapewnia potrzebnego wsparcia na własną rękę; takie propozycje nazywamy wspólnymi przesłankami. Rozważ, co następuje:

w tym argumencie ani przesłanka 1, ani przesłanka 2 nie popierają samego wniosku; raczej drugie przesłanka, niejako, zawiera klucz, który odblokowuje wniosek z przesłanki warunkowej 1. Takie współzależności możemy wskazać diagramowo za pomocą nawiasów, a więc:

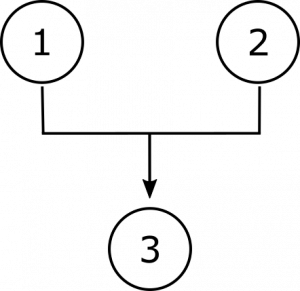
Diagramowanie argumentów w ten sposób może być pomocne zarówno w zrozumieniu ich działania, jak i informowaniu o wszelkich próbach krytycznego zaangażowania się w nie., W pierwszym argumencie wyraźnie widać, że jakiekolwiek argumenty przedstawione w sprzeczności z jednym z niezależnych przesłanek nie podważą całkowicie poparcia dla tego wniosku, ponieważ istnieje jeszcze inna przesłanka dająca mu pewien stopień poparcia. Jednak w drugim argumencie argumenty przemawiające przeciwko drugiej przesłance odciąłyby poparcie dla wniosku u jego źródła; a wszystko, co jest sprzeczne z pierwszą przesłanką, pozostawi drugą w potrzebie wsparcia. Natomiast w trzecim argumencie względy sprzeczne z którymkolwiek ze wspólnych przesłanek podważą poparcie dla tego wniosku., Zwłaszcza, gdy argumenty są bardziej złożone, takie wizualne pomoce mogą nam pomóc rozpoznać wszystkie wnioski zawarte w argumencie.

być może warto będzie zawrzeć rozważając nieco bardziej złożony argument. Rozważmy naturę liczb:

konkluzją tego argumentu jest ostatnia propozycja, że liczby są obiektami abstrakcyjnymi. Zauważ, że pierwsza przesłanka daje nam wybór między tym twierdzeniem a alternatywą—że są one konkretne. Druga przesłanka zaprzecza tej alternatywie, więc przesłanki 1 i 2 współpracują ze sobą, aby poprzeć wniosek:

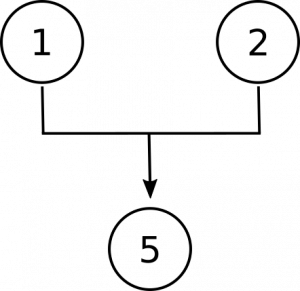
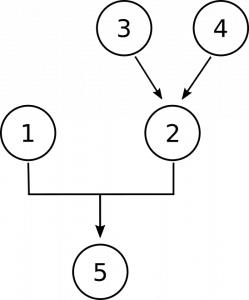
teraz musimy zrobić miejsce w naszym diagramie dla propozycji 3 i 4. Są po to, by dać nam powody, by wierzyć, że liczby nie są konkretnymi przedmiotami., Po pierwsze, twierdząc, że liczby nie znajdują się w przestrzeni, tak jak konkretne obiekty, a po drugie, twierdząc, że liczby nie oddziałują z innymi obiektami, tak jak konkretne obiekty. Są to osobne, niezależne powody, aby wierzyć, że nie są konkretne, więc kończymy z tym diagramem:

Logika i filozofia

sercem logicznego przedsięwzięcia jest filozoficzne pytanie: co sprawia, że dobry argument? Oznacza to, że co to jest dla zestawu roszczeń, aby zapewnić wsparcie dla jakiegoś innego roszczenia? A może: kiedy jesteśmy uzasadnieni w wyciąganiu wniosków?, Aby odpowiedzieć na te pytania, logicy opracowali szeroką gamę systemów logicznych, obejmujących różne rodzaje argumentów i stosując różne zasady i techniki. Wiele z narzędzi opracowanych w logice może być stosowanych poza granicami filozofii. Matematyk dowodzący twierdzeniem, informatyk programujący komputer, językoznawca modelujący strukturę języka – wszystko to za pomocą metod logicznych., Ponieważ logika ma tak szerokie zastosowanie i ze względu na formalne / matematyczne wyrafinowanie wielu systemów logicznych, zajmuje wyjątkowe miejsce w programie filozoficznym. Klasa logiki jest zazwyczaj w przeciwieństwie do innych klas filozofii, w tym bardzo mało czasu spędza się bezpośrednio angażując się i próbując odpowiedzieć na „wielkie pytania”; raczej, bardzo szybko sprowadza się do biznesu uczenia się logicznych formalizmów. Pytania, na które logika próbuje odpowiedzieć, są ważnymi pytaniami filozoficznymi, ale techniki opracowane, aby na nie odpowiedzieć, są godne samodzielnego studiowania.,

nie oznacza to jednak, że logika i filozofia powinny być ze sobą powiązane jedynie stycznie, przeciwnie, są ze sobą głęboko splecione. Dla wszystkich formalnych dzwonków i gwizdków opisywanych w najnowszym high-endowym systemie logicznym, na dole jest to część wysiłku, aby odpowiedzieć na fundamentalne pytanie, co z czego wynika. Co więcej, logika jest przydatna praktykującemu filozofowi na co najmniej trzy inne sposoby.

Filozofowie próbują odpowiedzieć na głębokie, drażliwe pytania—o naturę rzeczywistości, co stanowi dobre życie, jak tworzyć sprawiedliwe społeczeństwo itd., Udzielają odpowiedzi na te pytania i popierają je uzasadnieniem. Następnie inni filozofowie rozważają ich argumenty i odpowiadają opracowaniami i krytykami-argumentami własnymi. Filozofia jest prowadzona i czyni postępy poprzez wymianę argumentów. Ponieważ są one podstawowym narzędziem ich handlu, filozofowie lepiej wiedzieć trochę o tym, co sprawia, że dobre argumenty! Logika jest zatem niezbędna w praktyce filozofii.,

ale logika nie jest jedynie narzędziem oceny argumentów filozoficznych; zmieniła bieg toczącej się filozoficznej rozmowy. W miarę jak logicy rozwijali systemy formalne, aby modelować strukturę coraz szerszej gamy praktyk dyskursywnych, filozofowie byli w stanie zastosować swoje spostrzeżenia bezpośrednio do tradycyjnych problemów filozoficznych i rozpoznać wcześniej ukryte drogi dociekań. Zwłaszcza od przełomu XX wieku, rozprzestrzenianie się nowatorskich podejść w logice wywołało rewolucję w praktyce filozofii., Nie jest przesadą stwierdzenie, że znaczna część historii filozofii w XX wieku stanowiła nieustanną próbę zmierzenia się z nowymi osiągnięciami w logice i filozoficznym skupieniem na języku, którego wydawały się domagać. Żaden wątek filozoficzny—od metafizyki przez etykę po epistemologię i nie tylko—nie był nietknięty przez tę rewolucję.

wreszcie sama logika jest źródłem fascynujących pytań filozoficznych. Podstawowe pytanie w jego sercu-co to jest roszczenie do naśladowania od innych?,- rozchodzi się w niezliczonych kierunkach, dając żyzny grunt dla filozoficznych spekulacji. Jest logika, a potem jest filozofia logiki. Logika jest na przykład „formalna”. Co to znaczy? To zaskakująco trudne pytanie do odpowiedzi. Nasze najprostsze logiczne sformułowania zdań warunkowych (tych zawierających „jeśli”) prowadzą do pozornych paradoksów. Jak należy je rozwiązać? Czy nasze formalizmy powinny zostać zmienione, aby lepiej uchwycić naturalne znaczenia uwarunkowań? Jaki jest właściwie związek między systemami logicznymi a językami naturalnymi?,

tradycyjnie większość logików przyjmuje, że logika powinna być „dwuznaczna”: każda propozycja jest albo prawdziwa, albo fałszywa. Ale języki naturalne zawierają niejasne terminy, których granice zastosowania nie zawsze są jasne. Na przykład „łysy”: w przypadku niektórych przedmiotów możemy być skłonni powiedzieć, że są na dobrej drodze do pełnej łysiny, ale jeszcze nie do końca; z drugiej strony niechętnie powiemy, że nie są łysi. Są między nimi sprawy. W takich przypadkach możemy na przykład powiedzieć, że twierdzenie, że Fredo jest łysy, nie jest ani prawdziwe, ani fałszywe., Niektórzy logicy opracowali logiki, które nie są dwuznaczne, aby radzić sobie z tego rodzaju zjawiskiem językowym. Niektórzy dodają trzecią wartość prawdy: „Żadna” lub „nieokreślona”, na przykład. Inni wprowadzają nieskończone stopnie prawdy (nazywa się to „logiką rozmytą”). Te logiki odbiegają od tradycyjnych podejść. Czy zatem w pewnym sensie się mylą? Czy mają rację, a tradycjonaliści się mylą? Czy w ogóle zadajemy sensowne pytanie, kiedy zadajemy pytanie, czy dany system logiczny jest dobry, czy zły?, Czy możemy być tak zwanymi logicznymi „pluralistami”, akceptującymi różne niezgodne logiki, w zależności np. od tego, czy są one użyteczne?

tego rodzaju pytania wykraczają oczywiście poza zakres tego tekstu wprowadzającego. Są one zawarte, aby dać poczucie, jak daleko można podjąć naukę logiki. Zadaniem na razie jest jednak rozpoczęcie tego badania.