
Leonardo z Pizy (Fibonacci) (ok.1170-1250)
XIII-wieczny Włoski Leonardo z Pizy, lepiej znany pod pseudonimem Fibonacci był prawdopodobnie najbardziej utalentowanym zachodnim matematykiem średniowiecza. Niewiele wiadomo o jego życiu poza tym, że był synem urzędnika celnego i jako dziecko podróżował z ojcem po Afryce Północnej, gdzie uczył się arabskiej matematyki., Po powrocie do Włoch pomógł rozpowszechnić tę wiedzę w całej Europie, uruchamiając w ten sposób odmłodzenie w matematyce Europejskiej, która była w dużej mierze uśpiona przez wieki w średniowieczu.
w szczególności w 1202 roku napisał niezwykle wpływową książkę ” Liber Abaci „(„Księga obliczeń”), w której promował użycie hindusko-arabskiego systemu liczbowego, opisując jego wiele korzyści zarówno dla kupców, jak i matematyków w porównaniu z niezdarnym systemem rzymskich cyfr, używanym wówczas w Europie., Pomimo oczywistych zalet, upowszechnienie tego systemu w Europie było powolne (było to przecież w czasie krucjat przeciwko islamowi, w czasach, w których cokolwiek arabskiego było postrzegane z wielką podejrzliwością), a cyfry arabskie zostały nawet zakazane we Florencji w 1299 roku pod pretekstem, że były łatwiejsze do sfałszowania niż Cyfry rzymskie. Jednak zdrowy rozsądek ostatecznie zwyciężył i nowy system został przyjęty w całej Europie do 15 wieku, czyniąc System Rzymski przestarzały., W pracy tej po raz pierwszy użyto również poziomej notacji słupkowej dla ułamków (choć zgodnie z arabską praktyką umieszczania ułamka na lewo od liczby całkowitej).
ciąg Fibonacciego

odkrycie słynnej sekwencji Fibonacciego
Fibonacciego jest najbardziej znany, jednak, za jego wprowadzenie do Europy konkretnej sekwencji liczb, która stała się znana jako liczby Fibonacciego lub ciąg Fibonacciego., Odkrył sekwencję-pierwszą znaną w Europie rekurencyjną sekwencję liczb – rozważając w „Liber Abaci” problem praktyczny polegający na wzroście hipotetycznej populacji królików w oparciu o wyidealizowane założenia. Zauważył, że po każdym miesięcznym pokoleniu liczba par królików zwiększała się z 1 do 2 do 3 do 5 do 8 do 13 itd.i zidentyfikował postęp sekwencji, dodając dwa poprzednie terminy (w kategoriach matematycznych Fn = Fn-1 + Fn-2), sekwencję, która teoretycznie może rozciągać się w nieskończoność.,
sekwencja, która w rzeczywistości była znana indyjskim matematykom od VI wieku, ma wiele interesujących właściwości matematycznych, a wiele implikacji i związków sekwencji zostało odkrytych dopiero kilka wieków po śmierci Fibonacciego., Na przykład Sekwencja regeneruje się w zaskakujący sposób: co trzecia liczba F jest podzielna przez 2 (F3 = 2), co czwarta liczba F jest podzielna przez 3 (F4 = 3), co piąta liczba F jest podzielna przez 5 (F5 = 5), co szósta liczba F jest podzielna przez 8 (F6 = 8), co siódma liczba F jest podzielna przez 13 (F7 = 13) itd., Liczby sekwencji również okazały się wszechobecne w naturze: między innymi wiele gatunków roślin kwiatowych ma liczbę płatków w sekwencji Fibonacciego; spiralne układy ananasów występują w 5s i 8s, szyszki w 8s i 13s, a nasiona głów słonecznika w 21S, 34s, 55s lub nawet wyższych terminów w sekwencji; itp.,
Złoty Współczynnik φ
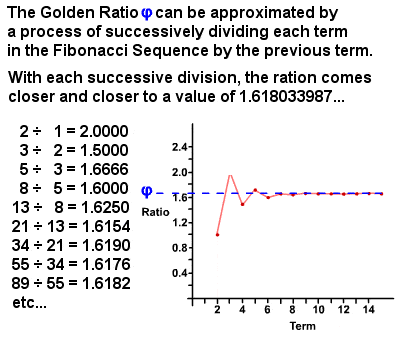
Złoty Współczynnik φ może być wyprowadzony z ciągu Fibonacciego
w 1750 roku Robert Simson zauważył, że stosunek każdego terminu w ciągu Fibonacciego do poprzedniego terminu zbliża się, z coraz większą dokładnością, im wyższe terminy, stosunek około 1 : 1.6180339887 (w rzeczywistości jest to liczba irracjonalna równa (1 + √5)⁄2, która została obliczona do tysięcy miejsc po przecinku)., Wartość ta jest określana jako złoty stosunek, znany również jako złota Średnia, Złota sekcja, Boska proporcja itp. i jest zwykle oznaczana grecką literą Phi φ(lub czasami wielką literą Phi Φ). Zasadniczo dwie ilości są w złotym stosunku, jeśli stosunek sumy ilości do większej ilości jest równy stosunkowi większej ilości do mniejszej. Sam złoty stosunek ma wiele unikalnych właściwości, takich jak 1 φ φ = φ – 1 (0,618…) i φ2 = φ + 1 (2,618…), i istnieje niezliczona ilość przykładów tego można znaleźć zarówno w przyrodzie, jak i w świecie ludzi.,
prostokąt o bokach w stosunku 1 : φ jest znany jako złoty prostokąt, a wielu artystów i architektów w całej historii (sięgającej starożytnego Egiptu i Grecji, ale szczególnie popularnej w sztuce renesansowej Leonarda da Vinci i jego współczesnych) proporcjonalnie swoje prace w przybliżeniu stosując złoty stosunek i Złote prostokąty, które są powszechnie uważane za z natury estetyczne. Łuk łączący przeciwległe punkty coraz mniejszych zagnieżdżonych Złotych prostokątów tworzy logarytmiczną spiralę, znaną jako złota spirala., Złoty stosunek i złota spirala można również znaleźć w zaskakującej liczbie instancji w przyrodzie, od muszli przez kwiaty, przez rogi zwierzęce, przez ludzkie ciała, przez systemy burzowe, aż po kompletne galaktyki.,
należy jednak pamiętać, że ciąg Fibonacciego był w rzeczywistości tylko bardzo drobnym elementem w „Liber Abaci” – w rzeczywistości ciąg otrzymał nazwę Fibonacciego dopiero w 1877 roku, kiedy Eduouard Lucas postanowił oddać mu hołd, nazywając serię jego imieniem – i że sam Fibonacci nie był odpowiedzialny za identyfikację żadnej z interesujących właściwości matematycznych ciągu, jego związku ze złotą średnią, złotymi prostokątami i spiralami itp.,
mnożenie krat
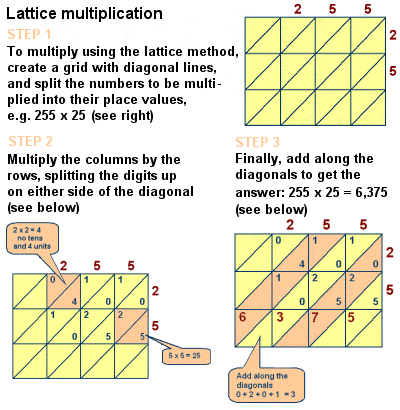
Fibonacci wprowadził mnożenie krat do Europy
jednak wpływ książki na średniowieczną matematykę jest niezaprzeczalny, a także zawiera dyskusje na temat wielu innych problemów matematycznych, takich jak Chińskie twierdzenie o pozostałościach, liczby doskonałe i pierwsze, wzory na szereg arytmetyczny i kwadratowe liczby piramidalne, euklidesowe dowody geometryczne oraz badanie równań liniowych równoległych wzdłuż linii diofantus i Al-karaji., Opisał również metodę mnożenia siatkowego (lub sitowego) mnożenia dużych liczb, metodę – pierwotnie pionierską przez islamskich matematyków, takich jak Al-Khwarizmi – algorytmicznie równoważną długim mnożeniu.
nie była też jedyna książka „Liber Abaci” Fibonacciego, choć była to jego najważniejsza., Jego „Liber Quadratorum” („Księga kwadratów”), na przykład, jest książką o algebrze, opublikowaną w 1225 roku, w której pojawia się twierdzenie o tym, co obecnie nazywa się tożsamością Fibonacciego-czasami znane również jako tożsamość Brahmagupty po znacznie wcześniejszym indyjskim matematyku, który również doszedł do tych samych wniosków – że iloczyn dwóch Sum dwóch kwadratów sam w sobie jest sumą dwóch kwadratów np. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |