efekty uczenia się
- zapoznaj się z historią pozycyjnych systemów liczbowych
- Zidentyfikuj bazy, które były używane w systemach liczbowych historycznie
- Konwertuj liczby między bazami
- użyj dwóch różnych metod konwersji liczb między bazami
Tło
jak można sobie wyobrazić, rozwój systemu bazowego jest ważnym krokiem w uczynieniu procesu liczenia bardziej wydajnym., Nasz własny system base-ten powstał prawdopodobnie z faktu, że mamy 10 palców (w tym kciuki) na dwóch dłoniach. Jest to naturalny rozwój. Jednak inne cywilizacje miały wiele baz innych niż dziesięć. Na przykład tubylcy z Queensland używali systemu base-two, licząc w następujący sposób: „one, two, two and one, two two' s, much.”Niektóre współczesne plemiona Ameryki Południowej mają system pięciu baz, licząc w ten sposób:” jeden, dwa, trzy, cztery, ręka, ręka i jeden, ręka i dwa ” i tak dalej. Babilończycy używali systemu bazodanowego (sexigesimal)., W tym rozdziale podsumowujemy konkretny przykład cywilizacji, która faktycznie używała systemu bazowego innego niż 10.
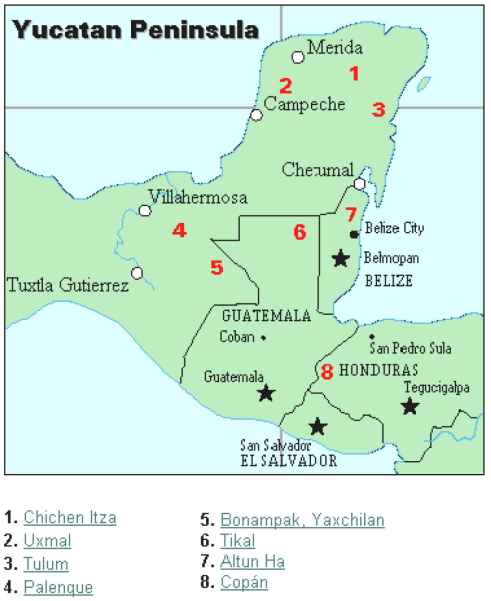cywilizacja Majów jest na ogół datowana od 1500 PNE do 1700 n. e. Półwysep Jukatan (patrz rysunek 16) w Meksyku był sceną rozwoju jednej z najbardziej zaawansowanych cywilizacji starożytnego świata. Majowie mieli wyrafinowany system rytualny, który był nadzorowany przez klasę kapłańską. Ta klasa kapłanów rozwinęła filozofię z czasem jako boską i wieczną., Kalendarz i związane z nim obliczenia były więc bardzo ważne dla rytualnego życia klasy kapłańskiej, a co za tym idzie ludu Majów. W rzeczywistości wiele z tego, co wiemy o tej kulturze, pochodzi z ich zapisów kalendarzowych i danych astronomicznych. Innym ważnym źródłem informacji na temat Majów są pisma Ojca Diego de Landa, który udał się do Meksyku jako misjonarz w 1549 roku.
były dwa systemy liczbowe opracowane przez Majów—jeden dla zwykłych ludzi i jeden dla kapłanów., Nie tylko te dwa systemy używały różnych symboli, ale także różnych systemów bazowych. Dla kapłanów system liczbowy był regulowany przez rytuał. Dni w roku uważano za bogów, więc formalnymi symbolami dni były dekorowane głowy, podobnie jak próbka po lewej stronie, ponieważ podstawowy kalendarz opierał się na 360 dniach, system liczb kapłańskich używał mieszanego systemu bazowego, wykorzystującego wielokrotności 20 i 360. Powoduje to mylący system, którego szczegóły pominiemy.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the „common” people, which used a more consistent base system., Jak pisaliśmy wcześniej, Majowie używali systemu base-20, zwanego systemem „vigesimal”. Podobnie jak nasz system, jest pozycyjny, co oznacza, że pozycja symbolu numerycznego wskazuje jego wartość miejsca. W poniższej tabeli możesz zobaczyć wartość place w formacie pionowym.
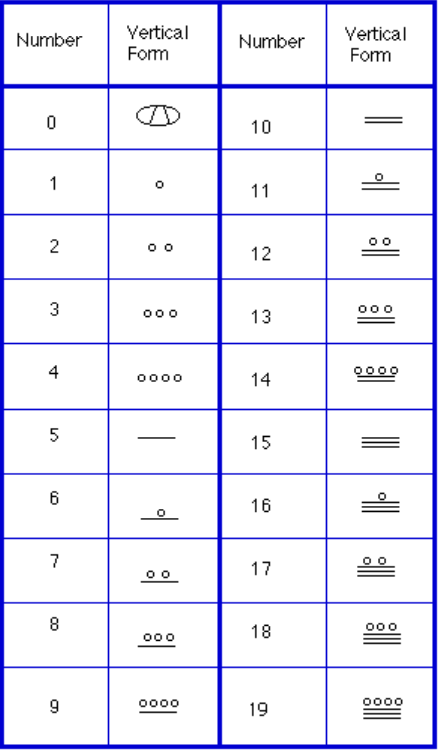
aby zapisać liczby, w tym systemie potrzebne były tylko trzy symbole. Pozioma belka reprezentuje ilość 5, kropka reprezentuje ilość 1, A specjalny symbol (uważany za powłokę) reprezentuje zero., System Majów mógł być pierwszym, który użył zera jako elementu zastępczego / liczby. Pierwsze 20 liczb pokazano w tabeli po prawej stronie.
W przeciwieństwie do naszego systemu, gdzie one miejsce zaczyna się po prawej stronie, a następnie przesuwa się w lewo, Systemy Majów umieszcza te na dole orientacji pionowej i przesuwa się w górę wraz ze wzrostem wartości miejsca.
gdy liczby są zapisywane w formie pionowej, nigdy nie powinno być więcej niż cztery kropki w jednym miejscu. Podczas pisania liczb Majów, każda grupa pięciu kropek staje się jednym słupkiem., Ponadto, nigdy nie powinno być więcej niż trzy takty w jednym miejscu … cztery takty zostaną zamienione na jedną kropkę w następnym miejscu. To tak samo, jak 10 jest zamieniane na 1 w następnym miejscu w górę, gdy nosimy podczas dodawania.
przykład
Jaka jest wartość tej liczby, która jest wyświetlana w formie pionowej?
przykład
Jaka jest wartość następującej liczby Majów?,
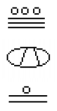
spróbuj
przekonwertuj liczbę Majów poniżej na bazę 10.,
przykład
Konwertuj bazę 10 numer 357510 do cyfr Majów.
zauważ, że w poprzednim przykładzie użyto nowej notacji, gdy pisaliśmy 8,18,1520. Przecinki między trzema liczbami 8, 18 i 15 oddzielają teraz wartości miejsc dla nas, abyśmy mogli je od siebie oddzielić. Użycie przecinków jest nieco inne niż w systemie dziesiętnym. Gdy zapisujemy liczbę w bazie 10, taką jak 7,567,323, przecinki są używane głównie jako pomoc do łatwego odczytu liczby, ale nie oddzielają wartości pojedynczych miejsc od siebie., Będziemy potrzebować tej notacji, gdy baza, której używamy, jest większa niż 10.
zapisywanie liczb z podstawami większymi niż 10
gdy podstawa liczby jest większa niż 10, oddziel każdą „cyfrę” przecinkiem, aby separacja cyfr była jasna.
na przykład w bazie 20 zapisujemy liczbę odpowiadającą 17 × 202 + 6 × 201 + 13 × 200, napiszemy 17,6,1320.
w poniższym filmie przedstawiamy więcej przykładów jak zapisywać liczby za pomocą cyfr Majów, a także Jak konwertować cyfry zapisane w języku Majów na formę bazy 10.,
następny film pokazuje więcej przykładów konwersji liczb bazowych 10 na liczby Majów.
Dodawanie liczb Majów
dodając liczby Majów razem, przyjmiemy schemat, który prawdopodobnie Majowie nie używali, ale który ułatwi nam życie.
przykład
Dodaj w Majów liczby 37 i 29:
wypróbuj to
spróbuj dodać 174 i 78 w Majów, najpierw konwertując liczby Majów, a następnie pracując całkowicie w tym systemie. Nie dodawaj w base-ten (dziesiętny) do samego końca, gdy sprawdzasz swoją pracę.
w ostatnim filmie pokazujemy więcej przykładów dodawania cyfr Majów.,
w tym module krótko naszkicowaliśmy rozwój liczb i naszego systemu liczenia, z naciskiem na Część „krótką”. Istnieje wiele źródeł informacji i badań, które wypełniają wiele tomów książek na ten temat. Niestety, nie możemy zbliżyć się do pokrycia wszystkich informacji, które tam są.
tylko zarysowaliśmy powierzchnię bogactwa badań i informacji, które istnieją na temat rozwoju liczb i liczenia w całej historii ludzkości., Co ważne, system, z którego korzystamy na co dzień, jest produktem tysięcy lat postępu i rozwoju. Reprezentuje wkład wielu cywilizacji i kultur. To nie zstąpi do nas z nieba, to dar od bogów. Nie jest to stworzenie wydawcy podręczników. Jest rzeczywiście tak samo ludzki jak my, podobnie jak reszta matematyki. Za każdym symbolem, formułą i regułą kryje się ludzkie oblicze, które można znaleźć, a przynajmniej szukać.
ponadto, mamy nadzieję, że teraz masz podstawowe uznanie dla tego, jak interesujące i różnorodne systemy liczbowe mogą uzyskać., Ponadto, jesteśmy prawie pewni, że zacząłeś również dostrzegać, że traktujemy nasz własny system liczbowy za pewnik tak bardzo, że kiedy próbujemy dostosować się do innych systemów lub baz, naprawdę musimy się skoncentrować i myśleć o tym, co się dzieje.