the 5 Clustering Algorithms Data Scientists Need to Know (Polski)

niedawno uruchomiłem biuletyn edukacyjny skupiający się na książkach. Book Dives to dwutygodnik, w którym dla każdego nowego numeru nurkujemy w książce non-fiction. Dowiesz się o podstawowych lekcjach książki i jak je zastosować w prawdziwym życiu. Możesz zapisać się na nią tutaj.

klastrowanie jest techniką uczenia maszynowego, która polega na grupowaniu punktów danych. Biorąc pod uwagę zbiór punktów danych, możemy użyć algorytmu grupowania, aby sklasyfikować każdy punkt danych do określonej grupy., W teorii, punkty danych, które są w tej samej grupie powinny mieć podobne właściwości i / lub cechy, podczas gdy punkty danych w różnych grupach powinny mieć bardzo różne właściwości i / lub cechy. Klastrowanie jest metodą uczenia się bez nadzoru i jest powszechną techniką analizy danych statystycznych używaną w wielu dziedzinach.

w analityce danych możemy wykorzystać analizę klastrów, aby uzyskać cenne informacje na temat naszych danych, sprawdzając, do jakich grup należą punkty danych, gdy zastosujemy algorytm klastrowania., Dzisiaj przyjrzymy się popularnym algorytmom klastrowania 5, które muszą znać naukowcy danych oraz ich zaletom i wadom!

K-oznacza klastrowanie

k-oznacza jest prawdopodobnie najbardziej znanym algorytmem klastrowania. Jest nauczany na wielu wprowadzających zajęciach z nauk o danych i uczenia maszynowego. Jest łatwy do zrozumienia i wdrożenia w kodzie! Sprawdź poniższą grafikę, aby uzyskać ilustrację.,

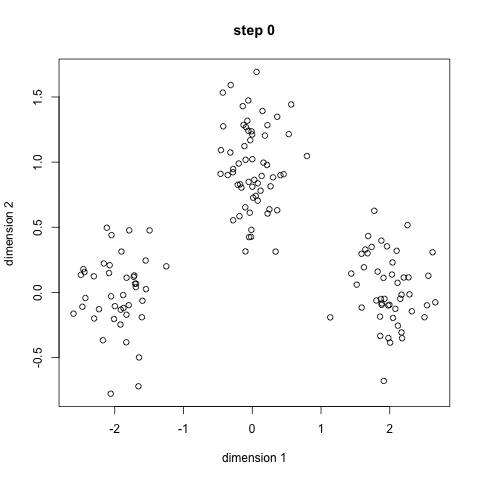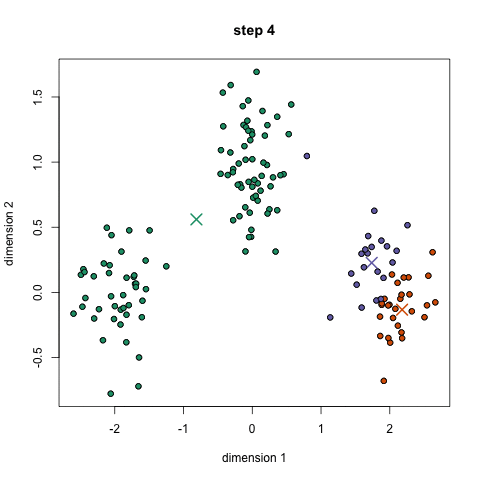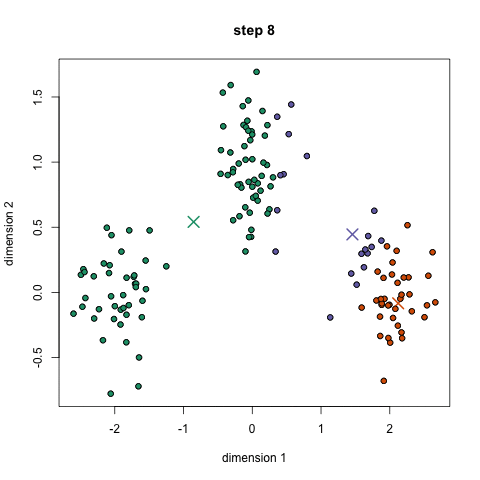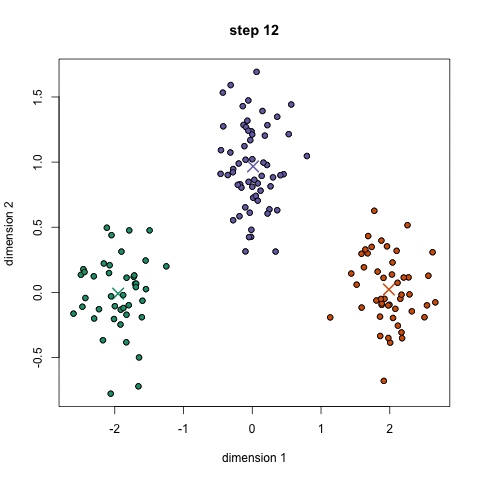
1. aby rozpocząć, najpierw wybieramy liczbę klas / grup do użycia i losowo inicjalizujemy ich odpowiednie punkty środkowe. Aby ustalić liczbę klas do użycia, Dobrze jest rzucić okiem na dane i spróbować zidentyfikować dowolne odrębne grupy. Punkty środkowe są wektorami tej samej długości co wektory punktów danych i są „X” na powyższej grafice.,
2. każdy punkt danych jest klasyfikowany przez Obliczanie odległości między tym punktem A każdym Centrum grupy, a następnie klasyfikowanie punktu w grupie, której centrum jest najbliżej niego.
3. na podstawie tych sklasyfikowanych punktów przeliczamy środek grupy, biorąc średnią wszystkich wektorów w grupie.
4. powtórz te kroki dla określonej liczby iteracji lub dopóki centra grup nie zmienią się zbytnio między iteracjami. Możesz również zdecydować się na losowo zainicjowanie centrów grup kilka razy, a następnie wybrać bieg, który wygląda tak, jakby zapewniał najlepsze wyniki.,

k-Means ma tę zaletę, że jest dość szybki, ponieważ wszystko, co tak naprawdę robimy, to Obliczanie odległości między punktami i centrami grupowymi; bardzo mało obliczeń! Ma więc złożoność liniową O (n).

z drugiej strony K-Means ma kilka wad. Po pierwsze, musisz wybrać, ile jest grup / klas. Nie zawsze jest to trywialne i najlepiej z algorytmu grupowania chcielibyśmy, aby dowiedzieć się tych dla nas, ponieważ chodzi o to, aby uzyskać pewien wgląd z danych., K-oznacza również rozpoczyna się od losowego wyboru centrów klastrów i dlatego może dawać różne wyniki klastrowania w różnych przebiegach algorytmu. Tak więc wyniki mogą nie być powtarzalne i brak spójności. Inne metody klastrowe są bardziej spójne.

k-mediany to kolejny algorytm klastrowania związany ze środkami K, z tym że zamiast przeliczać punkty środkowe grupy używając średniej używamy wektora mediany grupy., Metoda ta jest mniej wrażliwa na wartości odstające (ze względu na użycie mediany), ale jest znacznie wolniejsza dla większych zbiorów danych, ponieważ sortowanie jest wymagane na każdej iteracji podczas obliczania wektora mediany.

Mean-Shift clustering

Mean-shift clustering jest algorytmem opartym na przesuwanych oknach, który próbuje znaleźć gęste obszary punktów danych. Jest to algorytm oparty na centroid, co oznacza, że celem jest zlokalizowanie punktów środkowych każdej grupy / klasy, która działa poprzez aktualizację kandydatów na punkty środkowe, aby być średnią punktów w przesuwanym oknie., Te okna kandydatów są następnie filtrowane na etapie przetwarzania końcowego, aby wyeliminować prawie duplikaty, tworząc końcowy zestaw punktów środkowych i odpowiadających im grup. Sprawdź poniższą grafikę, aby uzyskać ilustrację.

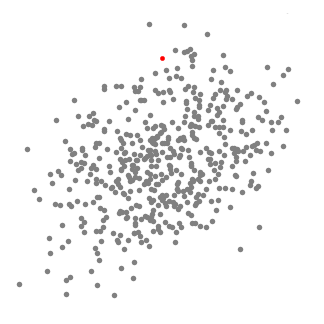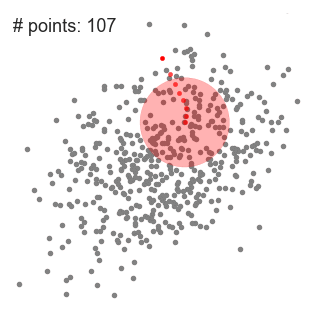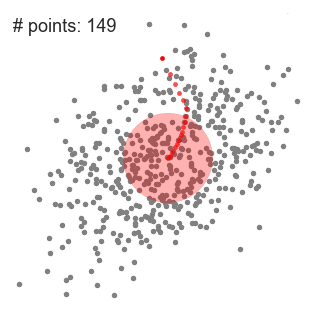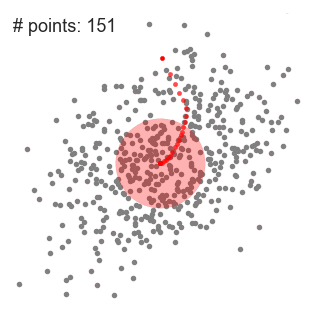
1. aby wyjaśnić przesunięcie średnie, rozważymy zbiór punktów w dwuwymiarowej przestrzeni, jak na powyższej ilustracji., Zaczynamy od okrągłego przesuwanego okna wyśrodkowanego w punkcie C (losowo wybranym) i mającego promień r jako jądro. Mean shift jest algorytmem wspinaczkowym, który polega na iteracyjnym przesunięciu tego jądra do regionu o większej gęstości na każdym kroku, aż do konwergencji.
2. przy każdej iteracji okno przesuwane przesuwa się w kierunku regionów o większej gęstości, przesuwając punkt środkowy do średniej punktów w oknie (stąd nazwa). Gęstość w oknie przesuwnym jest proporcjonalna do liczby punktów wewnątrz niego., Oczywiście, przesuwając się do średniej punktów w oknie będzie stopniowo przesuwać się w kierunku obszarów o wyższej gęstości punktów.
3. kontynuujemy przesuwanie okna przesuwanego zgodnie ze średnią, aż nie ma kierunku, w którym przesunięcie może pomieścić więcej punktów wewnątrz jądra. Sprawdź powyższą grafikę; przesuwamy okrąg aż nie będziemy już zwiększać gęstości (tj. liczby punktów w oknie).
4. ten proces kroków od 1 do 3 odbywa się z wieloma przesuwanymi oknami, aż wszystkie punkty leżą w oknie., Gdy wiele okien przesuwnych zachodzą na siebie, okno zawierające najwięcej punktów jest zachowywane. Punkty danych są następnie grupowane zgodnie z przesuwanym oknem, w którym się znajdują.

poniżej przedstawiono ilustrację całego procesu od końca do końca ze wszystkimi oknami przesuwnymi. Każda czarna kropka reprezentuje centroid przesuwanego okna, a każda szara kropka jest punktem danych.,

w przeciwieństwie do k-means clustering, nie ma potrzeby wyboru liczby klastrów, ponieważ mean-Shift automatycznie to wykrywa. To ogromna zaleta. Fakt, że centra klastra zbiegają się w kierunku punktów maksymalnej gęstości, jest również bardzo pożądany, ponieważ jest dość intuicyjny w zrozumieniu i pasuje dobrze w sensie naturalnie opartym na danych., Wadą jest to, że wybór rozmiaru/promienia okna ” r ” może być nietrywialny.

przestrzenne klastrowanie aplikacji z szumem oparte na gęstości (DBSCAN)

DBSCAN jest opartym na gęstości algorytmem klastrowym podobnym do mean-shift, ale z kilkoma znaczącymi zaletami. Sprawdź kolejną fantazyjną grafikę poniżej i zaczynajmy!,

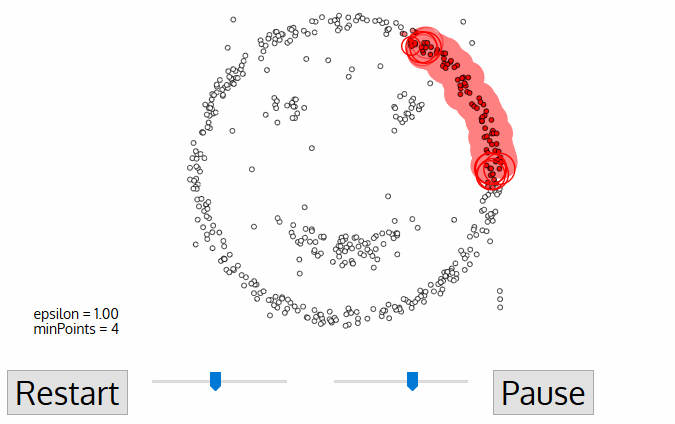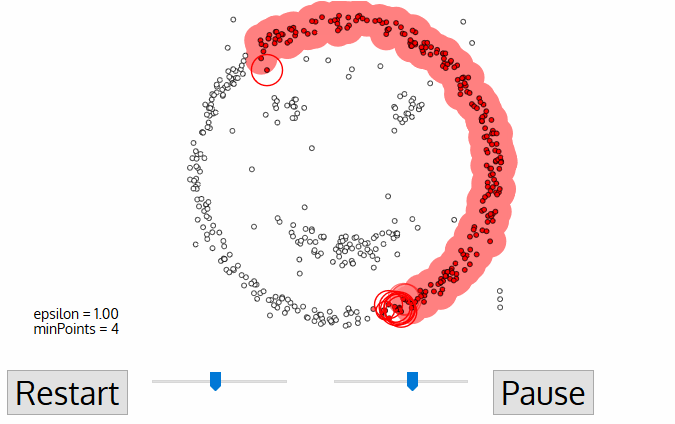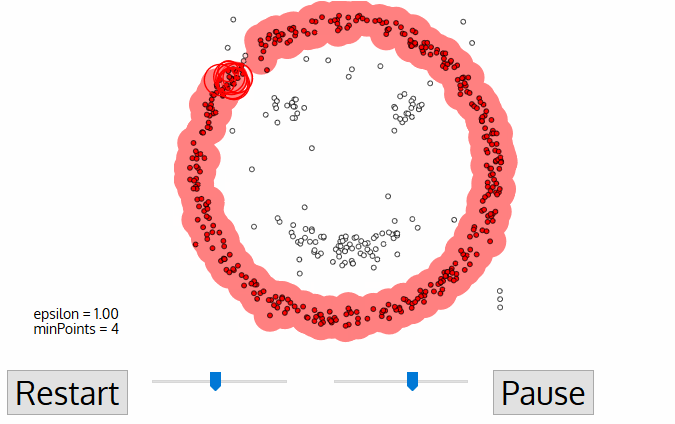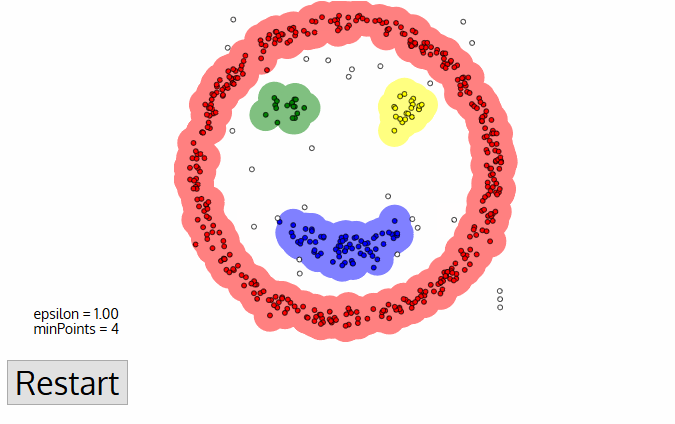
1. dbscan rozpoczyna się od dowolnego punktu początkowego, który nie został odwiedzony. Sąsiedztwo tego punktu jest wyodrębniane za pomocą odległości Epsilon ε (wszystkie punkty znajdujące się w odległości ε są punktami sąsiedztwa).,
2. jeżeli w tej okolicy znajduje się wystarczająca liczba punktów (według minPoints), wtedy rozpoczyna się proces klastrowania i bieżący punkt danych staje się pierwszym punktem w nowym klastrze. W przeciwnym razie punkt zostanie oznaczony jako szum (później ten hałaśliwy punkt może stać się częścią klastra). W obu przypadkach punkt ten oznaczany jest jako „odwiedzony”.
3. dla tego pierwszego punktu w nowej gromadzie punkty w jej sąsiedztwie odległości ε również stają się częścią tej samej gromady., Ta procedura sprawiania, że wszystkie punkty w sąsiedztwie ε należą do tego samego klastra jest następnie powtarzana dla wszystkich nowych punktów, które zostały właśnie dodane do grupy klastra.
4. ten proces kroków 2 i 3 jest powtarzany, dopóki wszystkie punkty w klastrze nie zostaną określone, tzn. wszystkie punkty w sąsiedztwie ε klastra zostaną odwiedzone i oznaczone.
5. Po Zakończeniu pracy z bieżącym klastrem, nowy nieodwiedziony punkt jest pobierany i przetwarzany, co prowadzi do odkrycia kolejnego klastra lub szumu. Proces ten powtarza się, dopóki wszystkie punkty nie zostaną Oznaczone jako odwiedzone., Ponieważ na koniec wszystkie punkty zostały odwiedzone, każdy punkt zostanie oznaczony jako należący do klastra lub będący szumem.

DBSCAN ma wiele zalet w stosunku do innych algorytmów klastrowania. Po pierwsze, nie wymaga w ogóle określonej liczby klastrów pe. Identyfikuje również odstające odgłosy jako szumy, w przeciwieństwie do Mean-shift, który po prostu wyrzuca je do klastra, nawet jeśli punkt danych jest bardzo różny. Dodatkowo może znaleźć dowolnie wielkości i dowolnie ukształtowane klastry dość dobrze.,

główną wadą DBSCAN jest to, że nie działa tak dobrze jak inne, gdy klastry mają różną gęstość. Dzieje się tak, ponieważ ustawienie progu odległości ε i minPoints do identyfikacji punktów sąsiedztwa będzie się różnić w zależności od klastra do klastra, gdy gęstość się zmienia. Wada ta występuje również w przypadku bardzo dużych wymiarów danych, ponieważ ponownie próg odległości ε staje się trudny do oszacowania.,

oczekiwanie–maksymalizacja (EM) klastrowanie przy użyciu modeli mieszanek Gaussa (GMM)

jedną z głównych wad K-Means jest naiwne wykorzystanie średniej wartości dla Centrum klastra. Możemy zobaczyć, dlaczego nie jest to najlepszy sposób na robienie rzeczy, patrząc na poniższy obrazek. Po lewej stronie, wydaje się dość oczywiste dla ludzkiego oka, że istnieją dwie okrągłe gromady o różnym promieniu ' wyśrodkowane w tej samej średniej. K-oznacza nie może sobie z tym poradzić, ponieważ średnie wartości klastrów są bardzo blisko siebie., K-oznacza również niepowodzenie w przypadkach, gdy klastry nie są okrągłe, ponownie w wyniku użycia średniej jako środka klastra.

modele mieszanek Gaussa (GMM) dają nam większą elastyczność niż środki K. W przypadku GMMs Zakładamy, że punkty danych są rozłożone Gaussa; jest to mniej restrykcyjne założenie niż twierdzenie, że są okrągłe za pomocą średniej., W ten sposób mamy dwa parametry opisujące kształt klastrów: średnią i odchylenie standardowe! Biorąc przykład w dwóch wymiarach, oznacza to, że klastry mogą przyjmować dowolny kształt eliptyczny (ponieważ mamy odchylenie standardowe zarówno w kierunkach x, jak i y). Tak więc każdy rozkład Gaussa jest przypisany do jednego klastra.

aby znaleźć parametry Gaussa dla każdego klastra (np. średnią i odchylenie standardowe), użyjemy algorytmu optymalizacyjnego zwanego oczekiwaniem-maksymalizacją (EM)., Spójrz na poniższą grafikę jako ilustrację gaussy są dopasowane do gromad. Następnie możemy przystąpić do procesu grupowania oczekiwań-maksymalizacji przy użyciu GMM.

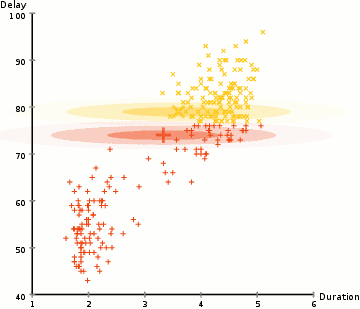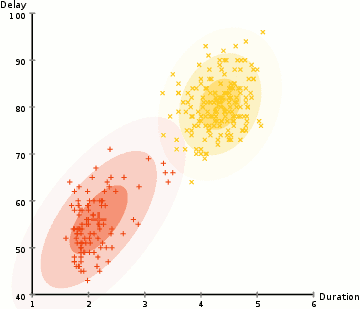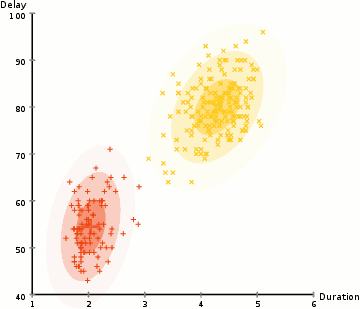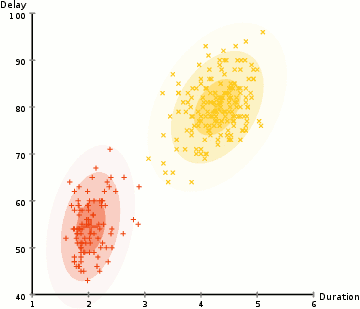
1. zaczynamy od wybrania liczby klastrów (tak jak robi to k-means) I losowo inicjalizujemy parametry rozkładu Gaussa dla każdego klastra., Można spróbować zapewnić dobry guesstimate dla początkowych parametrów, biorąc szybki rzut oka na dane zbyt. Chociaż należy zauważyć, jak widać na powyższej grafice, nie jest to w 100% konieczne, ponieważ Gaussowie zaczynają Nasze jako bardzo słabe, ale są szybko zoptymalizowane.
2. biorąc pod uwagę te rozkłady Gaussa dla każdego klastra, Oblicz prawdopodobieństwo, że każdy punkt danych należy do określonego klastra. Im bliżej punktu znajduje się centrum Gaussa, tym bardziej prawdopodobne jest, że należy do tej gromady., Powinno to mieć intuicyjny sens, ponieważ z rozkładem Gaussa Zakładamy, że większość danych leży bliżej centrum klastra.
3. na podstawie tych prawdopodobieństw obliczamy nowy zestaw parametrów dla rozkładów Gaussa, tak aby zmaksymalizować prawdopodobieństwo punktów danych w klastrach. Obliczamy te nowe parametry za pomocą ważonej sumy pozycji punktów danych, gdzie wagi są prawdopodobieństwami punktu danych należącego do danego klastra., Aby wyjaśnić to wizualnie, możemy spojrzeć na powyższą grafikę, w szczególności na żółty klaster jako przykład. Dystrybucja zaczyna się losowo na pierwszej iteracji, ale widzimy, że większość żółtych punktów znajduje się po prawej stronie tej dystrybucji. Kiedy obliczamy sumę ważoną prawdopodobieństwem, mimo że w pobliżu środka znajdują się punkty, większość z nich znajduje się po prawej stronie. W ten sposób w naturalny sposób średnia rozkładu jest przesunięta bliżej tych zbiorów punktów. Widzimy również, że większość punktów jest „od góry od prawej do dołu od lewej”., Dlatego odchylenie standardowe zmienia się, tworząc elipsę, która jest bardziej dopasowana do tych punktów, aby zmaksymalizować sumę ważoną prawdopodobieństwem.
4. kroki 2 i 3 są powtarzane iteracyjnie aż do konwergencji, gdzie dystrybucje nie zmieniają się zbytnio z iteracji na iterację.

istnieją 2 kluczowe zalety korzystania z GMM. Po pierwsze GMM są dużo bardziej elastyczne pod względem kowariancji klastra niż K-oznacza; ze względu na parametr odchylenia standardowego, klastry mogą przybierać dowolny kształt elipsy, zamiast być ograniczone do okręgów., K-oznacza w rzeczywistości szczególny przypadek GMM, w którym KOWARIANCJA każdego klastra wzdłuż wszystkich wymiarów zbliża się do 0. Po drugie, ponieważ GMM używają prawdopodobieństw, mogą mieć wiele klastrów na punkt danych. Więc jeśli punkt danych znajduje się w środku dwóch nakładających się klastrów, możemy po prostu zdefiniować jego klasę, mówiąc, że należy X-procent do klasy 1 i y-procent do klasy 2. Czyli GMM wspierają mieszane członkostwo.

aglomeracyjne hierarchiczne klastry

algorytmy klastrowania hierarchicznego dzielą się na 2 kategorie: top-down lub bottom-up., Algorytmy oddolne traktują każdy punkt danych jako pojedynczy klaster na początku, a następnie kolejno scalają (lub aglomeratuj) pary klastrów, aż wszystkie klastry zostaną połączone w jeden klaster, który zawiera wszystkie punkty danych. Hierarchiczne grupowanie od dołu do góry nazywa się więc hierarchicznym aglomeracyjnym grupowaniem lub HAC. Ta hierarchia gromad jest reprezentowana jako drzewo (lub dendrogram). Korzeń drzewa jest unikalnym skupiskiem, które gromadzi wszystkie próbki, liście są skupiskami z tylko jedną próbką., Sprawdź poniższą grafikę, aby uzyskać ilustrację, zanim przejdziesz do kroków algorytmu

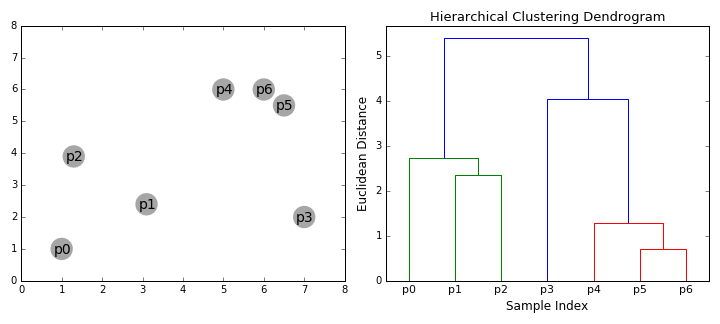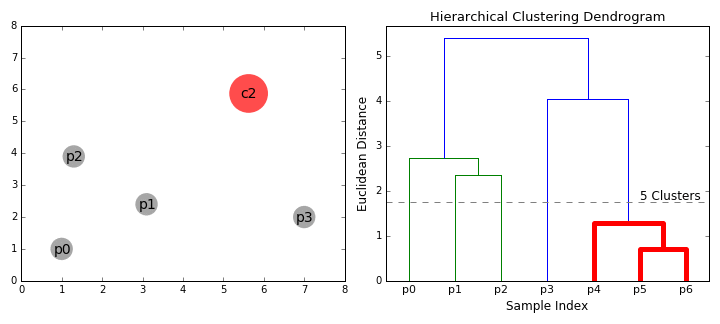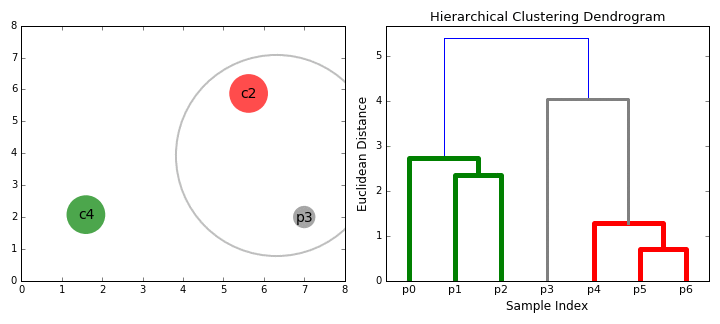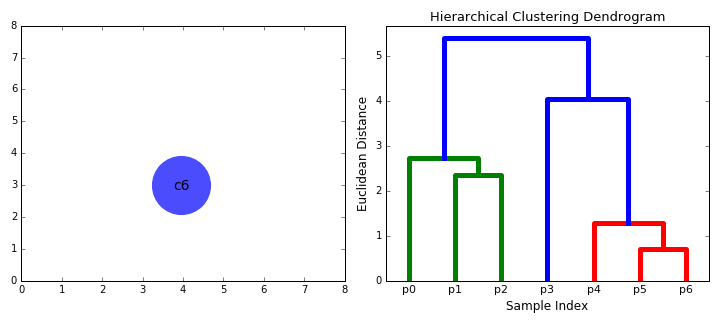
1. zaczynamy od traktowania każdego punktu danych jako pojedynczego klastra tzn. jeśli w naszym zbiorze danych znajdują się X punkty danych, to mamy x klastry. Następnie wybieramy metrykę odległości, która mierzy odległość między dwoma gromadami., Jako przykład użyjemy średniego powiązania, które definiuje odległość między dwoma klastrami jako średnią odległość między punktami danych w pierwszym klastrze i punktami danych w drugim klastrze.
2. na każdej iteracji łączymy dwa klastry w jeden. Dwa klastry, które mają być połączone, są wybierane jako te o najmniejszym średnim powiązaniu. Tj. zgodnie z naszą wybraną metryką odległości, te dwa klastry mają najmniejszą odległość między sobą, a zatem są najbardziej podobne i powinny być łączone.
3. Krok 2 powtarzamy aż dotrzemy do korzenia drzewa i.,e mamy tylko jeden klaster, który zawiera wszystkie punkty danych. W ten sposób możemy wybrać, ile klastrów chcemy w końcu, po prostu wybierając, kiedy przestać łączyć klastry tzn. kiedy przestaniemy budować drzewo!

hierarchiczne klastry nie wymagają od nas podawania liczby klastrów, a nawet możemy wybrać, która liczba klastrów wygląda najlepiej, ponieważ budujemy drzewo. Dodatkowo algorytm nie jest wrażliwy na wybór metryki odległości; wszystkie z nich działają równie dobrze, podczas gdy z innymi algorytmami klastrowania, wybór metryki odległości jest krytyczny., Szczególnie dobrym przypadkiem użycia hierarchicznych metod klastrowania jest sytuacja, gdy podstawowe dane mają hierarchiczną strukturę i chcesz odzyskać hierarchię; inne algorytmy klastrowania nie mogą tego zrobić. Te zalety hierarchicznego klastrowania są kosztem niższej wydajności, ponieważ ma złożoność czasową O (n3), w przeciwieństwie do złożoności liniowej K-Means I GMM.